Questa pagina è stata tradotta dall'API Cloud Translation.

Trasformazioni WebGL

Gregg Tavares

Traduzione 2D WebGL

Prima di passare al 3D, continuiamo a lavorare in 2D per un po' di tempo. Abbi pazienza. Questo articolo potrebbe sembrare estremamente ovvio per alcuni, ma arriverò a un punto in alcuni articoli.

Questo articolo è la continuazione di una serie che inizia con Nozioni di base su WebGL. Se non l'hai letto, ti consiglio di leggere almeno il primo capitolo e poi tornare qui. La traduzione è un nome matematico complicato che significa essenzialmente "spostare" qualcosa. Suppongo che anche il trasferimento di una frase dall'inglese al giapponese sia appropriato, ma in questo caso parliamo di spostamento della geometria. Utilizzando il codice di esempio che abbiamo ottenuto nel primo post, puoi tradurre facilmente il nostro rettangolo semplicemente modificando i valori passati a setRectangle, giusto? Ecco un esempio basato sul nostro esempio precedente.

  // First lets make some variables 
  // to hold the translation of the rectangle
  var translation = [0, 0];
  // then let's make a function to
  // re-draw everything. We can call this
  // function after we update the translation.
  // Draw the scene.
  function drawScene() {
     // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);
    // Setup a rectangle
    setRectangle(gl, translation[0], translation[1], width, height);

    // Draw the rectangle.
    gl.drawArrays(gl.TRIANGLES, 0, 6);
  }

Fin qui tutto bene. Ora immagina di voler fare la stessa cosa con una forma più complicata. Supponiamo di voler disegnare una "F" composta da 6 triangoli come questo.

Ecco il codice attuale che dovremmo modificare impostando setRectangle su qualcosa di più simile a questo.

// Fill the buffer with the values that define a letter 'F'.
function setGeometry(gl, x, y) {
  var width = 100;
  var height = 150;
  var thickness = 30;
  gl.bufferData(
      gl.ARRAY_BUFFER,
      new Float32Array([
          // left column
          x, y,
          x + thickness, y,
          x, y + height,
          x, y + height,
          x + thickness, y,
          x + thickness, y + height,

          // top rung
          x + thickness, y,
          x + width, y,
          x + thickness, y + thickness,
          x + thickness, y + thickness,
          x + width, y,
          x + width, y + thickness,

          // middle rung
          x + thickness, y + thickness * 2,
          x + width * 2 / 3, y + thickness * 2,
          x + thickness, y + thickness * 3,
          x + thickness, y + thickness * 3,
          x + width * 2 / 3, y + thickness * 2,
          x + width * 2 / 3, y + thickness * 3]),
      gl.STATIC_DRAW);
}

Spero che tu capisca che non funzionerà bene. Se vogliamo disegnare una geometria molto complessa con centinaia o migliaia di linee, dobbiamo scrivere un codice piuttosto complesso. Inoltre, ogni volta che disegniamo, JavaScript deve aggiornare tutti i punti. Esiste un modo più semplice. Carica la geometria ed esegui la traduzione nello shader. Ecco il nuovo shader

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform vec2 u_translation;

void main() {
   // Add in the translation.
   vec2 position = a_position + u_translation;

   // convert the rectangle from pixels to 0.0 to 1.0
   vec2 zeroToOne = position / u_resolution;
   ...

e ristrutturare un po' il codice. Ad esempio, dobbiamo impostare la geometria una sola volta.

// Fill the buffer with the values that define a letter 'F'.
function setGeometry(gl) {
  gl.bufferData(
      gl.ARRAY_BUFFER,
      new Float32Array([
          // left column
          0, 0,
          30, 0,
          0, 150,
          0, 150,
          30, 0,
          30, 150,

          // top rung
          30, 0,
          100, 0,
          30, 30,
          30, 30,
          100, 0,
          100, 30,

          // middle rung
          30, 60,
          67, 60,
          30, 90,
          30, 90,
          67, 60,
          67, 90]),
      gl.STATIC_DRAW);
}

Poi dobbiamo solo aggiornare u_translation prima di disegnare con la traduzione che preferiamo.

  ...
  var translationLocation = gl.getUniformLocation(
             program, "u_translation");
  ...
  // Set Geometry.
  setGeometry(gl);
  ..
  // Draw scene.
  function drawScene() {
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Set the translation.
    gl.uniform2fv(translationLocation, translation);

    // Draw the rectangle.
    gl.drawArrays(gl.TRIANGLES, 0, 18);
  }

Tieni presente che setGeometry viene chiamato una sola volta. Non è più all'interno di drawScene.

Ora, quando disegniamo, WebGL fa praticamente tutto. Non facciamo altro che impostare una traduzione e chiedergli di disegnare. Anche se la nostra geometria avesse decine di migliaia di punti, il codice principale rimarrebbe invariato.

Rotazione 2D WebGL

Lo ammetto subito, non ho idea se la mia spiegazione avrà senso, ma tanto vale provare.

Per prima cosa, voglio presentarti quello che si chiama "circolo unitario". Se ricordi la matematica delle scuole medie (non addormentarti!), un cerchio ha un raggio. Il raggio di un cerchio è la distanza dal centro del cerchio al bordo. Un cerchio unitario è un cerchio con raggio 1.

Se ricordi la matematica di base della terza elementare, se moltiplichi qualcosa per 1, il risultato rimane invariato. Quindi 123 * 1 = 123. È un gioco da ragazzi, no? Un cerchio unitario, un cerchio con raggio 1, 0 è anche una forma di 1. È un 1 in rotazione. Quindi puoi moltiplicare qualcosa per questo cerchio unitario e in un certo senso è un po' come moltiplicare per 1, tranne per il fatto che accade la magia e le cose ruotano. Prenderemo i valori X e Y di qualsiasi punto del cerchio unitario e li moltiplicheremo per la geometria del nostro campione precedente. Ecco gli aggiornamenti al nostro shader.

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;

void main() {
  // Rotate the position
  vec2 rotatedPosition = vec2(
     a_position.x * u_rotation.y + a_position.y * u_rotation.x,
     a_position.y * u_rotation.y - a_position.x * u_rotation.x);

  // Add in the translation.
  vec2 position = rotatedPosition + u_translation;

Aggiorniamo il codice JavaScript in modo da poter passare questi due valori.

  ...
  var rotationLocation = gl.getUniformLocation(program, "u_rotation");
  ...
  var rotation = [0, 1];
  ..
  // Draw the scene.
  function drawScene() {
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Set the translation.
    gl.uniform2fv(translationLocation, translation);

    // Set the rotation.
    gl.uniform2fv(rotationLocation, rotation);

    // Draw the rectangle.
    gl.drawArrays(gl.TRIANGLES, 0, 18);
  }

Perché funziona? Dai, dai un'occhiata ai calcoli.

rotatedX = a_position.x * u_rotation.y + a_position.y * u_rotation.x;
rotatedY = a_position.y * u_rotation.y - a_position.x * u_rotation.x;

Supponiamo che tu abbia un rettangolo e che tu voglia ruotarlo. Prima di iniziare a ruotarlo, l'angolo in alto a destra è a 3,0, 9,0. Scegliamo un punto sul cerchio unitario a 30 gradi in senso orario rispetto alle ore 12.

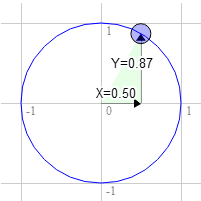
La posizione sul cerchio è 0,50 e 0,87

3.0 * 0.87 + 9.0 * 0.50 = 7.1
9.0 * 0.87 - 3.0 * 0.50 = 6.3

È esattamente dove deve essere

Lo stesso per 60 gradi in senso orario

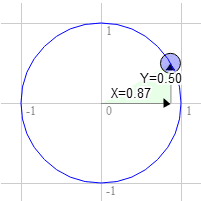
La posizione sul cerchio è 0,87 e 0,50

3.0 * 0.50 + 9.0 * 0.87 = 9.3
9.0 * 0.50 - 3.0 * 0.87 = 1.9

Puoi vedere che, ruotando il punto in senso orario verso destra, il valore X aumenta e quello Y diminuisce. Se continui oltre i 90 gradi, X inizierà a diminuire di nuovo e Y inizierà ad aumentare. Questo pattern ci dà la rotazione. I punti su un cerchio unitario hanno un altro nome. Si chiamano seno e coseno. Quindi, per un determinato angolo, possiamo semplicemente cercare il seno e il coseno in questo modo.

function printSineAndCosineForAnAngle(angleInDegrees) {
  var angleInRadians = angleInDegrees * Math.PI / 180;
  var s = Math.sin(angleInRadians);
  var c = Math.cos(angleInRadians);
  console.log("s = " + s + " c = " + c);
}

Se copi e incolli il codice nella console JavaScript e digiti printSineAndCosignForAngle(30), viene stampato s = 0.49 c= 0.87 (nota: ho arrotondato i numeri). Se li combini tutti, puoi ruotare la geometria a qualsiasi angolazione. Basta impostare la rotazione sul seno e sul coseno dell'angolo a cui vuoi ruotare.

  ...
  var angleInRadians = angleInDegrees * Math.PI / 180;
  rotation[0] = Math.sin(angleInRadians);
  rotation[1] = Math.cos(angleInRadians);

Spero che queste informazioni ti siano state utili. Ecco un'altra domanda più semplice. Scala.

Che cosa sono i radianti?

I radianti sono un'unità di misura utilizzata con cerchi, rotazioni e angoli. Proprio come possiamo misurare la distanza in pollici, iarde, metri e così via, possiamo misurare gli angoli in gradi o radianti.

Probabilmente sai che i calcoli con le misure metriche sono più semplici di quelli con le misure imperiali. Per passare da pollici a piedi, dividiamo per 12. Per passare da pollici a yard, dividiamo per 36. Non so tu, ma io non riesco a dividere per 36 a mente. Con il sistema metrico è molto più facile. Per passare da millimetri a centimetri, dividiamo per 10. Per passare da millimetri a metri, dividiamo per 1000. Posso dividere per 1000 a mente.

I radianti e i gradi sono simili. I gradi rendono i calcoli difficili. I radianti semplificano i calcoli. Un cerchio ha 360 gradi, ma solo 2π radianti. Quindi un giro completo è pari a 2π radianti. Un mezzo giro equivale a π radianti. Un quarto di giro, ovvero 90 gradi, corrisponde a π/2 radianti. Quindi, se vuoi ruotare qualcosa di 90 gradi, utilizza Math.PI * 0.5. Se vuoi ruotarlo di 45 gradi, usa Math.PI * 0.25 e così via.

Quasi tutti i calcoli che coinvolgono angoli, cerchi o rotazioni sono molto semplici se inizi a pensare in radianti. Provaci. Utilizza i radianti, non i gradi, tranne che nelle visualizzazioni dell'interfaccia utente.

Scala 2D WebGL

Il ridimensionamento è facile come la traduzione.

Moltiplichiamo la posizione per la scala che ci interessa. Ecco le modifiche rispetto al nostro esempio precedente.

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;
uniform vec2 u_scale;

void main() {
  // Scale the positon
  vec2 scaledPosition = a_position * u_scale;

  // Rotate the position
  vec2 rotatedPosition = vec2(
     scaledPosition.x * u_rotation.y +
        scaledPosition.y * u_rotation.x,
     scaledPosition.y * u_rotation.y -
        scaledPosition.x * u_rotation.x);

  // Add in the translation.
  vec2 position = rotatedPosition + u_translation;

e aggiungiamo il codice JavaScript necessario per impostare la scala durante il disegno.

  ...
  var scaleLocation = gl.getUniformLocation(program, "u_scale");
  ...
  var scale = [1, 1];
  ...
  // Draw the scene.
  function drawScene() {
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Set the translation.
    gl.uniform2fv(translationLocation, translation);

    // Set the rotation.
    gl.uniform2fv(rotationLocation, rotation);

    // Set the scale.
    gl.uniform2fv(scaleLocation, scale);

    // Draw the rectangle.
    gl.drawArrays(gl.TRIANGLES, 0, 18);
  }

Tieni presente che la scalatura per un valore negativo capovolge la geometria. Spero che questi ultimi 3 capitoli ti siano stati utili per comprendere la traslazione, la rotazione e la scala. Successivamente, esamineremo la magia delle matrici che combinano tutti e tre questi elementi in una forma molto più semplice e spesso più utile.

Perché una "F"?

La prima volta che ho visto qualcuno usare una "F" era su una trama. La lettera "F" stessa non è importante. L'importante è che tu possa capire l'orientamento da qualsiasi direzione. Se utilizzassimo un cuore ♥ o un triangolo △, ad esempio, non potremmo capire se è stato capovolto orizzontalmente. Un cerchio ○ sarebbe ancora peggio. Un rettangolo colorato potrebbe funzionare con colori diversi su ogni angolo, ma poi dovresti ricordare quale angolo è quale. L'orientamento di una F è immediatamente riconoscibile.

Puoi utilizzare qualsiasi forma di cui conosci l'orientamento. Io uso la F da quando ho iniziato a utilizzare questa idea.

Matrici 2D WebGL

Negli ultimi 3 capitoli abbiamo esaminato come tradurre, ruotare e ridimensionare la geometria. La traslazione, la rotazione e la scala sono considerate ciascuna un tipo di "trasformazione". Ognuna di queste trasformazioni richiedeva modifiche allo shader e ognuna delle tre dipendeva dall'ordine.

Ad esempio, ecco una scala di 2, 1, una rotazione del 30% e una traslazione di 100, 0.

Ecco una traslazione di 100,0, una rotazione del 30% e una scala di 2, 1

I risultati sono completamente diversi. Peggio ancora, se avessimo bisogno del secondo esempio, dovremmo scrivere uno shader diverso che applichi la traslazione, la rotazione e la scala nel nuovo ordine desiderato. Beh, alcune persone molto più intelligenti di me hanno capito che puoi fare tutto lo stesso con la matematica delle matrici. Per 2D utilizziamo una matrice 3x3. Una matrice 3x3 è come una griglia con 9 caselle.

1.0	2.0	3,0
4.0	5,0	6,0
7,0	8.0	9.0

Per eseguire i calcoli, moltiplichiamo la posizione per le colonne della matrice e sommiamo i risultati. Le nostre posizioni hanno solo due valori, x e y, ma per fare questo calcolo abbiamo bisogno di tre valori, quindi utilizzeremo 1 per il terzo valore. In questo caso il risultato sarà

newX = x * 1.0 + y * 4.0 + 1 * 7.0

newY = x * 2.0 + y * 5.0 + 1 * 8.0

extra = x * 3.0 + y * 6.0 + 1 * 9.0

Probabilmente stai guardando questa pagina e ti stai chiedendo "A COSA SERVE?". Supponiamo di avere una traduzione. Chiameremo l'importo che vogliamo tradurre tx e ty. Creiamo una matrice come questa

1.0	0.0	0.0
0.0	1,0	0.0
tx	ty	1.0

Dai un'occhiata

newX = x * 1.0 + y * 0.0 + 1 * tx

newY = x * 0.0 + y * 1.0 + 1 * ty

extra = x * 0.0 + y * 0.0 + 1 * 1

Se ricordi l'algebra, possiamo eliminare qualsiasi numero moltiplicato per zero. La moltiplicazione per 1 non fa nulla, quindi semplifica per vedere cosa succede

newX = x + tx;
newY = y + ty;

E gli extra che non ci interessano molto. Sembra sorprendentemente simile al codice di traduzione del nostro esempio di traduzione. Analogamente, vediamo come funziona la rotazione. Come abbiamo sottolineato nel post sulla rotazione, ci occorrono solo la seno e la coseno dell'angolo attorno al quale vogliamo ruotare.

s = Math.sin(angleToRotateInRadians);
c = Math.cos(angleToRotateInRadians);

e creiamo una matrice come questa

c	-s	0.0
s	c	0.0
0.0	0.0	1.0

Applicando la matrice otteniamo

newX = x * c + y * s + 1 * 0

newY = x * -s + y * c + 1 * 0

extra = x * 0.0 + y * 0.0 + 1 * 1

Se copriamo tutti i prodotti per 0 e 1, otteniamo

newX = x *  c + y * s;
newY = x * -s + y * c;

È esattamente quello che avevamo nel nostro campione di rotazione. E infine la scalabilità. Chiameremo i due fattori di scala sx e sy e creeremo una matrice come questa

sx	0.0	0.0
0.0	sy	0.0
0.0	0.0	1.0

Applicando la matrice otteniamo

newX = x * sx + y * 0 + 1 * 0

newY = x * 0 + y * sy + 1 * 0

extra = x * 0.0 + y * 0.0 + 1 * 1

che è davvero

newX = x * sx;
newY = y * sy;

che è lo stesso del nostro esempio di scalabilità. Ora, sono sicuro che potresti ancora pensare. E quindi? Qual è il punto. Sembra un bel po' di lavoro solo per fare la stessa cosa che facevamo già. Ed è qui che entra in gioco la magia. A quanto pare, possiamo moltiplicare le matrici e applicare tutte le trasformazioni contemporaneamente. Supponiamo di avere la funzione matrixMultiply che prende due matrici, le moltiplica e restituisce il risultato. Per chiarire, creiamo delle funzioni per creare matrici per traslazione, rotazione e scala.

function makeTranslation(tx, ty) {
  return [
    1, 0, 0,
    0, 1, 0,
    tx, ty, 1
  ];
}

function makeRotation(angleInRadians) {
  var c = Math.cos(angleInRadians);
  var s = Math.sin(angleInRadians);
  return [
    c,-s, 0,
    s, c, 0,
    0, 0, 1
  ];
}

function makeScale(sx, sy) {
  return [
    sx, 0, 0,
    0, sy, 0,
    0, 0, 1
  ];
}

Ora cambiamo lo shader. Il vecchio shader aveva questo aspetto

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;
uniform vec2 u_scale;

void main() {
  // Scale the positon
  vec2 scaledPosition = a_position * u_scale;

  // Rotate the position
  vec2 rotatedPosition = vec2(
     scaledPosition.x * u_rotation.y + scaledPosition.y * u_rotation.x,
     scaledPosition.y * u_rotation.y - scaledPosition.x * u_rotation.x);

  // Add in the translation.
  vec2 position = rotatedPosition + u_translation;
  ...

Il nostro nuovo shader sarà molto più semplice.

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform mat3 u_matrix;

void main() {
  // Multiply the position by the matrix.
  vec2 position = (u_matrix * vec3(a_position, 1)).xy;
  ...

Ecco come la utilizziamo

  // Draw the scene.
  function drawScene() {
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Compute the matrices
    var translationMatrix =
       makeTranslation(translation[0], translation[1]);
    var rotationMatrix = makeRotation(angleInRadians);
    var scaleMatrix = makeScale(scale[0], scale[1]);

    // Multiply the matrices.
    var matrix = matrixMultiply(scaleMatrix, rotationMatrix);
    matrix = matrixMultiply(matrix, translationMatrix);

    // Set the matrix.
    gl.uniformMatrix3fv(matrixLocation, false, matrix);

    // Draw the rectangle.
    gl.drawArrays(gl.TRIANGLES, 0, 18);
  }

Potresti chiederti, e allora? Non mi sembra un vantaggio . Ora, però, se vogliamo cambiare l'ordine non dobbiamo scrivere un nuovo shader. Possiamo semplicemente cambiare i calcoli.

    ...
    // Multiply the matrices.
    var matrix = matrixMultiply(translationMatrix, rotationMatrix);
    matrix = matrixMultiply(matrix, scaleMatrix);
    ...

La possibilità di applicare matrici come questa è particolarmente importante per l'animazione gerarchica, ad esempio braccia su un corpo, lune su un pianeta attorno a un sole o rami su un albero. Per un semplice esempio di animazione gerarchica, disegniamo la nostra "F" 5 volte, ma ogni volta iniziamo con la matrice della "F" precedente.

  // Draw the scene.
  function drawScene() {
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Compute the matrices
    var translationMatrix = makeTranslation(translation[0], translation[1]);
    var rotationMatrix = makeRotation(angleInRadians);
    var scaleMatrix = makeScale(scale[0], scale[1]);

    // Starting Matrix.
    var matrix = makeIdentity();

    for (var i = 0; i < 5; ++i) {
      // Multiply the matrices.
      matrix = matrixMultiply(matrix, scaleMatrix);
      matrix = matrixMultiply(matrix, rotationMatrix);
      matrix = matrixMultiply(matrix, translationMatrix);

      // Set the matrix.
      gl.uniformMatrix3fv(matrixLocation, false, matrix);

      // Draw the geometry.
      gl.drawArrays(gl.TRIANGLES, 0, 18);
    }
  }

Per farlo, abbiamo introdotto la funzione makeIdentity, che crea una matrice di identità. Una matrice di identità è una matrice che rappresenta effettivamente 1,0, quindi se la moltiplichi per l'identità non succede nulla. Proprio come

X * 1 = X

così

matrixX * identity = matrixX

Ecco il codice per creare una matrice di identità.

function makeIdentity() {
  return [
    1, 0, 0,
    0, 1, 0,
    0, 0, 1
  ];
}

Un altro esempio: in tutti i sample finora la nostra "F" ruota attorno al suo angolo in alto a sinistra. Questo perché la matematica che utilizziamo ruota sempre attorno all'origine e l'angolo in alto a sinistra di "F" si trova nell'origine, (0, 0). Ora, però, poiché possiamo eseguire operazioni matematiche con le matrici e scegliere l'ordine in cui vengono applicate le trasformazioni, possiamo spostare l'origine prima dell'applicazione del resto delle trasformazioni.

    // make a matrix that will move the origin of the 'F' to
    // its center.
    var moveOriginMatrix = makeTranslation(-50, -75);
    ...

    // Multiply the matrices.
    var matrix = matrixMultiply(moveOriginMatrix, scaleMatrix);
    matrix = matrixMultiply(matrix, rotationMatrix);
    matrix = matrixMultiply(matrix, translationMatrix);

Con questa tecnica puoi ruotare o ridimensionare da qualsiasi punto. Ora sai come Photoshop o Flash ti consentono di spostare il punto di rotazione. Facciamo ancora di più. Se torniamo al primo articolo sui concetti di base di WebGL, potresti ricordare che abbiamo del codice nello shader per convertire da pixel a spazio clip che ha il seguente aspetto.

  ...
  // convert the rectangle from pixels to 0.0 to 1.0
  vec2 zeroToOne = position / u_resolution;

  // convert from 0->1 to 0->2
  vec2 zeroToTwo = zeroToOne * 2.0;

  // convert from 0->2 to -1->+1 (clipspace)
  vec2 clipSpace = zeroToTwo - 1.0;

  gl_Position = vec4(clipSpace * vec2(1, -1), 0, 1);

Se esamini ciascuno di questi passaggi, il primo, "converti da pixel a 0,0 a 1,0", è in realtà un'operazione di scala. Anche la seconda è un'operazione di scala. Il successivo è una traslazione e l'ultimo scala Y per -1. Possiamo farlo tutto nella matrice che passiamo allo shader. Potremmo creare due matrici di scala, una per la scala 1,0/risoluzione, un'altra per la scala 2,0, una terza per la traduzione di -1,0, -1,0 e una quarta per la scala Y di -1, quindi moltiplicarle tutte insieme, ma, poiché la matematica è semplice, creeremo semplicemente una funzione che genera direttamente una matrice di "proiezione" per una determinata risoluzione.

function make2DProjection(width, height) {
  // Note: This matrix flips the Y axis so that 0 is at the top.
  return [
    2 / width, 0, 0,
    0, -2 / height, 0,
    -1, 1, 1
  ];
}

Ora possiamo semplificare ulteriormente lo shader. Ecco l'intero nuovo shader vertex.

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform mat3 u_matrix;

void main() {
  // Multiply the position by the matrix.
  gl_Position = vec4((u_matrix * vec3(a_position, 1)).xy, 0, 1);
}
</script>

In JavaScript dobbiamo moltiplicare per la matrice di proiezione

  // Draw the scene.
  function drawScene() {
    ...
    // Compute the matrices
    var projectionMatrix =
       make2DProjection(canvas.width, canvas.height);
    ...

    // Multiply the matrices.
    var matrix = matrixMultiply(scaleMatrix, rotationMatrix);
    matrix = matrixMultiply(matrix, translationMatrix);
    matrix = matrixMultiply(matrix, projectionMatrix);
    ...
  }

Abbiamo anche rimosso il codice che imposta la risoluzione. Con questo ultimo passaggio siamo passati da uno shader piuttosto complicato con 6-7 passaggi a uno shader molto semplice con un solo passaggio, il tutto grazie alla magia della matematica matriciale.

Spero che questo articolo ti abbia aiutato a demistificare la matematica delle matrici. Ora passerò al 3D. In 3D, la matematica delle matrici segue gli stessi principi e lo stesso utilizzo. Ho iniziato con il 2D per semplificare la comprensione.