WebGL 2D 변환
3D로 넘어가기 전에 2D를 조금 더 살펴보겠습니다. 잠시만 기다려 주세요. 이 도움말은 일부 사용자에게는 너무 당연해 보일 수 있지만 몇 개의 도움말을 통해 점진적으로 설명해 드리겠습니다.
이 도움말은 WebGL 기초로 시작된 시리즈의 연속입니다. 아직 읽지 않았다면 최소한 첫 번째 챕터를 읽은 후 다시 돌아오세요. 변환은 기본적으로 '무언가를 이동'하는 것을 의미하는 멋진 수학 용어입니다. 영어에서 일본어로 문장을 이동하는 것도 적합하지만, 이 경우 도형을 이동하는 것을 말합니다. 첫 번째 게시물에서 만든 샘플 코드를 사용하면 setRectangle에 전달된 값을 변경하기만 하면 직사각형을 쉽게 변환할 수 있습니다. 다음은 이전 샘플을 기반으로 한 샘플입니다.
// First lets make some variables
// to hold the translation of the rectangle
var translation = [0, 0];
// then let's make a function to
// re-draw everything. We can call this
// function after we update the translation.
// Draw the scene.
function drawScene() {
// Clear the canvas.
gl.clear(gl.COLOR_BUFFER_BIT);
// Setup a rectangle
setRectangle(gl, translation[0], translation[1], width, height);
// Draw the rectangle.
gl.drawArrays(gl.TRIANGLES, 0, 6);
}
지금까지는 좋습니다. 하지만 이제 더 복잡한 도형으로 동일한 작업을 한다고 가정해 보겠습니다. 다음과 같이 6개의 삼각형으로 구성된 'F'를 그리고 싶다고 가정해 보겠습니다.

다음은 현재 코드입니다. setRectangle을 다음과 같이 변경해야 합니다.
// Fill the buffer with the values that define a letter 'F'.
function setGeometry(gl, x, y) {
var width = 100;
var height = 150;
var thickness = 30;
gl.bufferData(
gl.ARRAY_BUFFER,
new Float32Array([
// left column
x, y,
x + thickness, y,
x, y + height,
x, y + height,
x + thickness, y,
x + thickness, y + height,
// top rung
x + thickness, y,
x + width, y,
x + thickness, y + thickness,
x + thickness, y + thickness,
x + width, y,
x + width, y + thickness,
// middle rung
x + thickness, y + thickness * 2,
x + width * 2 / 3, y + thickness * 2,
x + thickness, y + thickness * 3,
x + thickness, y + thickness * 3,
x + width * 2 / 3, y + thickness * 2,
x + width * 2 / 3, y + thickness * 3]),
gl.STATIC_DRAW);
}
확장하기에 적합하지 않다는 것을 알 수 있습니다. 수백 또는 수천 개의 선으로 매우 복잡한 도형을 그리려면 꽤 복잡한 코드를 작성해야 합니다. 또한 그릴 때마다 JavaScript가 모든 점을 업데이트해야 합니다. 더 간단한 방법이 있습니다. 도형을 업로드하고 셰이더에서 변환을 실행하면 됩니다. 새 셰이더
<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;
uniform vec2 u_resolution;
uniform vec2 u_translation;
void main() {
// Add in the translation.
vec2 position = a_position + u_translation;
// convert the rectangle from pixels to 0.0 to 1.0
vec2 zeroToOne = position / u_resolution;
...
코드를 약간 재구성해 보겠습니다. 하나는 도형을 한 번만 설정하면 됩니다.
// Fill the buffer with the values that define a letter 'F'.
function setGeometry(gl) {
gl.bufferData(
gl.ARRAY_BUFFER,
new Float32Array([
// left column
0, 0,
30, 0,
0, 150,
0, 150,
30, 0,
30, 150,
// top rung
30, 0,
100, 0,
30, 30,
30, 30,
100, 0,
100, 30,
// middle rung
30, 60,
67, 60,
30, 90,
30, 90,
67, 60,
67, 90]),
gl.STATIC_DRAW);
}
그런 다음 원하는 변환으로 그리기 전에 u_translation를 업데이트하기만 하면 됩니다.
...
var translationLocation = gl.getUniformLocation(
program, "u_translation");
...
// Set Geometry.
setGeometry(gl);
..
// Draw scene.
function drawScene() {
// Clear the canvas.
gl.clear(gl.COLOR_BUFFER_BIT);
// Set the translation.
gl.uniform2fv(translationLocation, translation);
// Draw the rectangle.
gl.drawArrays(gl.TRIANGLES, 0, 18);
}
setGeometry는 한 번만 호출됩니다. 더 이상 drawScene 내에 있지 않습니다.
이제 그리면 WebGL이 거의 모든 작업을 실행합니다. 번역을 설정하고 그리도록 요청하는 것뿐입니다. 도형에 수만 개의 점이 있더라도 기본 코드는 동일하게 유지됩니다.
WebGL 2D 회전
제가 설명하는 방식이 이해하기 쉬울지 모르겠지만 일단 시도해 보겠습니다.
먼저 '단위 원'을 소개해 드리겠습니다. 중학교 수학을 기억한다면 (졸지 마세요!) 원에는 반지름이 있습니다. 원의 반지름은 원의 중심에서 가장자리까지의 거리입니다. 단위 원은 반지름이 1.0인 원입니다.
3학년 수학에서 배운 것처럼 1을 곱하면 값이 동일하게 유지됩니다. 따라서 123 * 1 = 123입니다. 간단하죠? 단위 원, 즉 반지름이 1.0인 원도 1의 한 형태입니다. 회전하는 1입니다. 따라서 이 단위 원을 사용하여 곱할 수 있으며, 마법이 일어나고 사물이 회전하는 점을 제외하고는 1을 곱하는 것과 비슷합니다. 단위 원의 임의 지점에서 X 및 Y 값을 가져와 이전 샘플의 도형에 곱합니다. 셰이더 업데이트 사항은 다음과 같습니다.
<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;
uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;
void main() {
// Rotate the position
vec2 rotatedPosition = vec2(
a_position.x * u_rotation.y + a_position.y * u_rotation.x,
a_position.y * u_rotation.y - a_position.x * u_rotation.x);
// Add in the translation.
vec2 position = rotatedPosition + u_translation;
그리고 이 두 값을 전달할 수 있도록 JavaScript를 업데이트합니다.
...
var rotationLocation = gl.getUniformLocation(program, "u_rotation");
...
var rotation = [0, 1];
..
// Draw the scene.
function drawScene() {
// Clear the canvas.
gl.clear(gl.COLOR_BUFFER_BIT);
// Set the translation.
gl.uniform2fv(translationLocation, translation);
// Set the rotation.
gl.uniform2fv(rotationLocation, rotation);
// Draw the rectangle.
gl.drawArrays(gl.TRIANGLES, 0, 18);
}
효과가 있는 이유는 무엇인가요? 수학적으로 따져 보세요.
rotatedX = a_position.x * u_rotation.y + a_position.y * u_rotation.x;
rotatedY = a_position.y * u_rotation.y - a_position.x * u_rotation.x;
직사각형이 있고 이를 회전하려고 한다고 가정해 보겠습니다. 회전을 시작하기 전에 오른쪽 상단은 3.0, 9.0입니다. 단위 원의 12시에서 시계 방향으로 30도 떨어진 지점을 선택해 보겠습니다.
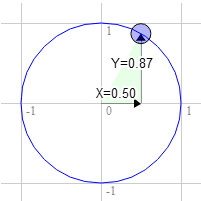
원 위의 위치는 0.50 및 0.87입니다.
3.0 * 0.87 + 9.0 * 0.50 = 7.1
9.0 * 0.87 - 3.0 * 0.50 = 6.3
바로 그 위치에 있어야 합니다.

시계 방향으로 60도 회전도 마찬가지입니다.
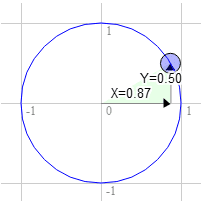
원 위의 위치는 0.87 및 0.50입니다.
3.0 * 0.50 + 9.0 * 0.87 = 9.3
9.0 * 0.50 - 3.0 * 0.87 = 1.9
이 점을 시계 방향으로 오른쪽으로 회전하면 X 값이 커지고 Y 값이 작아지는 것을 볼 수 있습니다. 90도를 지나 계속 진행하면 X가 다시 작아지고 Y가 커지기 시작합니다. 이 패턴을 사용하면 회전을 얻을 수 있습니다. 단위 원의 점에는 다른 이름이 있습니다. 사인과 코사인이라고 합니다. 따라서 주어진 각도에 대해 다음과 같이 사인과 코사인을 조회하면 됩니다.
function printSineAndCosineForAnAngle(angleInDegrees) {
var angleInRadians = angleInDegrees * Math.PI / 180;
var s = Math.sin(angleInRadians);
var c = Math.cos(angleInRadians);
console.log("s = " + s + " c = " + c);
}
코드를 복사하여 JavaScript 콘솔에 붙여넣고 printSineAndCosignForAngle(30)를 입력하면 s = 0.49 c= 0.87가 출력됩니다 (참고: 숫자를 반올림했습니다).
이를 모두 결합하면 도형을 원하는 각도로 회전할 수 있습니다. 회전을 회전하려는 각도의 사인과 코사인으로 설정하면 됩니다.
...
var angleInRadians = angleInDegrees * Math.PI / 180;
rotation[0] = Math.sin(angleInRadians);
rotation[1] = Math.cos(angleInRadians);
이해하기 쉬웠기를 바랍니다. 다음은 더 간단한 예시입니다. 확장하기
라디안이란 무엇인가요?
라디안은 원, 회전, 각도에 사용되는 측정 단위입니다. 거리를 인치, 야드, 미터 등으로 측정할 수 있는 것처럼 각도도 도 또는 라디안으로 측정할 수 있습니다.
미터법을 사용한 수학이 영국식 측정법을 사용한 수학보다 쉽다는 것을 알고 계실 것입니다. 인치에서 피트로 변환하려면 12로 나눕니다. 인치에서 야드로 변환하려면 36으로 나눕니다. 모르겠지만 저는 머릿속으로 36으로 나눌 수 없습니다. 측정항목을 사용하면 훨씬 쉽습니다. 밀리미터에서 센티미터로 변환하려면 10으로 나눕니다. 밀리미터를 미터로 변환하려면 1,000으로 나눕니다. 머릿속으로 1,000으로 나눌 수 있습니다.
라디안과 도도 비슷합니다. 도 단위로 계산하면 어렵습니다. 라디안을 사용하면 계산이 간단해집니다. 원에는 360도이지만 라디안으로는 2π만 있습니다. 따라서 한 바퀴는 2π라디안입니다. 반바퀴는 π 라디안입니다. 1/4 회전(90도)은 π/2라디안입니다. 따라서 90도 회전하려면 Math.PI * 0.5를 사용하면 됩니다. 45도 회전하려면 Math.PI * 0.25 등을 사용합니다.
각도, 원 또는 회전과 관련된 거의 모든 수학은 라디안으로 생각하면 매우 간단하게 작동합니다. 한번 사용해 보세요. UI 디스플레이를 제외하고는 도 아닌 라디안을 사용하세요.
WebGL 2D 크기 조정
확장도 번역만큼 간단합니다.
위치에 원하는 크기를 곱합니다. 이전 샘플과 변경된 사항은 다음과 같습니다.
<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;
uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;
uniform vec2 u_scale;
void main() {
// Scale the positon
vec2 scaledPosition = a_position * u_scale;
// Rotate the position
vec2 rotatedPosition = vec2(
scaledPosition.x * u_rotation.y +
scaledPosition.y * u_rotation.x,
scaledPosition.y * u_rotation.y -
scaledPosition.x * u_rotation.x);
// Add in the translation.
vec2 position = rotatedPosition + u_translation;
그리고 그릴 때 크기를 설정하는 데 필요한 JavaScript를 추가합니다.
...
var scaleLocation = gl.getUniformLocation(program, "u_scale");
...
var scale = [1, 1];
...
// Draw the scene.
function drawScene() {
// Clear the canvas.
gl.clear(gl.COLOR_BUFFER_BIT);
// Set the translation.
gl.uniform2fv(translationLocation, translation);
// Set the rotation.
gl.uniform2fv(rotationLocation, rotation);
// Set the scale.
gl.uniform2fv(scaleLocation, scale);
// Draw the rectangle.
gl.drawArrays(gl.TRIANGLES, 0, 18);
}
한 가지 주목할 점은 음수 값으로 크기를 조정하면 도형이 뒤집힌다는 것입니다. 마지막 3개 챕터가 변환, 회전, 크기 조정을 이해하는 데 도움이 되었기를 바랍니다. 다음으로, 이 세 가지를 훨씬 더 간단하고 종종 더 유용한 형태로 결합하는 매트릭스의 마법을 살펴보겠습니다.
'F'는 왜 사용되나요?
'F'를 처음 본 것은 텍스처였습니다. 'F' 자체는 중요하지 않습니다. 중요한 것은 어느 방향에서든 방향을 알 수 있다는 것입니다. 예를 들어 하트 ♥ 또는 삼각형 △을 사용하면 가로로 뒤집었는지 알 수 없습니다. 원 ○은 더 나쁩니다. 색상 직사각형은 각 모서리에 다른 색상을 사용해도 되지만, 그러면 어느 모서리가 어느 모서리인지 기억해야 합니다. F의 방향은 바로 알아볼 수 있습니다.

방향을 알 수 있는 모양이면 무엇이든 사용할 수 있습니다. 저는 이 아이디어를 처음 접했을 때부터 'F'를 사용해 왔습니다.
WebGL 2D 행렬
지난 3개 챕터에서는 도형을 변환하고, 도형을 회전하고, 도형의 크기를 조절하는 방법을 살펴봤습니다. 변환, 회전, 배율은 각각 '변환'의 한 유형으로 간주됩니다. 이러한 각 변환에는 셰이더를 변경해야 했으며 3가지 변환은 순서에 종속되었습니다.
예를 들어 다음은 크기가 2, 1이고, 회전이 30%이며, 변환이 100, 0인 경우입니다.

다음은 변환 100,0, 회전 30%, 배율 2, 1입니다.

결과는 완전히 다릅니다. 더 나쁜 것은 두 번째 예시가 필요한 경우 원하는 새 순서대로 변환, 회전, 크기 조정을 적용하는 다른 셰이더를 작성해야 한다는 점입니다. 저보다 훨씬 똑똑한 사람들이 행렬 수학으로도 똑같은 작업을 할 수 있다는 것을 알아냈습니다. 2d의 경우 3x3 행렬을 사용합니다. 3x3 매트릭스는 9개의 상자가 있는 그리드와 같습니다.
| 1.0 | 2.0 | 3.0 |
| 4.0 | 5.0 | 6.0 |
| 7.0 | 8.0 | 9.0 |
계산을 위해 행렬의 열 아래에 있는 위치를 곱한 다음 결과를 더합니다. 위치에는 x와 y라는 두 개의 값만 있지만 이 수학을 하려면 3개의 값이 필요하므로 세 번째 값으로 1을 사용합니다. 이 경우 결과는 다음과 같습니다.
newX = x * 1.0 + y * 4.0 + 1 * 7.0
newY = x * 2.0 + y * 5.0 + 1 * 8.0
extra = x * 3.0 + y * 6.0 + 1 * 9.0
'이게 무슨 의미야?'라고 생각하실 수도 있습니다. 번역이 있다고 가정해 보겠습니다. 변환하려는 금액을 tx 및 ty라고 합니다. 다음과 같은 행렬을 만들어 보겠습니다.
| 1.0 | 0.0 | 0.0 |
| 0.0 | 1.0 | 0.0 |
| tx | ty | 1.0 |
이제 확인해 보세요.
newX = x * 1.0 + y * 0.0 + 1 * tx
newY = x * 0.0 + y * 1.0 + 1 * ty
extra = x * 0.0 + y * 0.0 + 1 * 1
대수학을 기억하고 있다면 0으로 곱하는 부분을 삭제할 수 있습니다. 1을 곱하면 아무 일도 일어나지 않으므로 단순화하여 어떤 일이 일어나는지 확인해 보겠습니다.
newX = x + tx;
newY = y + ty;
그리고 그 외에는 크게 신경 쓰지 않습니다. 놀랍게도 번역 예의 번역 코드와 유사합니다. 마찬가지로 회전을 해 보겠습니다. 회전 게시물에서 지적했듯이 회전하려는 각도의 사인과 코사인만 있으면 됩니다.
s = Math.sin(angleToRotateInRadians);
c = Math.cos(angleToRotateInRadians);
다음과 같은 행렬을 빌드합니다.
| c | -s | 0.0 |
| s | c | 0.0 |
| 0.0 | 0.0 | 1.0 |
행렬을 적용하면 다음과 같이 표시됩니다.
newX = x * c + y * s + 1 * 0
newY = x * -s + y * c + 1 * 0
extra = x * 0.0 + y * 0.0 + 1 * 1
0과 1로 곱한 부분을 모두 지우면 다음과 같이 표시됩니다.
newX = x * c + y * s;
newY = x * -s + y * c;
이는 회전 샘플에서 확인할 수 있습니다. 마지막으로 확장성입니다. 두 배율 인수를 sx 및 sy라고 하고 다음과 같은 행렬을 빌드합니다.
| sx | 0.0 | 0.0 |
| 0.0 | sy | 0.0 |
| 0.0 | 0.0 | 1.0 |
행렬을 적용하면 다음과 같이 표시됩니다.
newX = x * sx + y * 0 + 1 * 0
newY = x * 0 + y * sy + 1 * 0
extra = x * 0.0 + y * 0.0 + 1 * 1
정말
newX = x * sx;
newY = y * sy;
이는 확장 샘플과 동일합니다.
아직도 고민하고 계실 수 있습니다. 그럼 어떻게 해야 하나요? 요점은 무엇인가요? 이미 하고 있는 것과 동일한 작업을 하기 위해 이렇게 많은 작업을 해야 하나요?
바로 이 지점에서 마법이 시작됩니다. 매트릭스를 곱하여 모든 변환을 한 번에 적용할 수 있습니다. 두 개의 행렬을 사용하여 곱한 후 결과를 반환하는 함수 matrixMultiply가 있다고 가정해 보겠습니다.
더 명확하게 이해할 수 있도록 변환, 회전, 크기 조정의 행렬을 빌드하는 함수를 만들어 보겠습니다.
function makeTranslation(tx, ty) {
return [
1, 0, 0,
0, 1, 0,
tx, ty, 1
];
}
function makeRotation(angleInRadians) {
var c = Math.cos(angleInRadians);
var s = Math.sin(angleInRadians);
return [
c,-s, 0,
s, c, 0,
0, 0, 1
];
}
function makeScale(sx, sy) {
return [
sx, 0, 0,
0, sy, 0,
0, 0, 1
];
}
이제 셰이더를 변경해 보겠습니다. 이전 셰이더는 다음과 같았습니다.
<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;
uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;
uniform vec2 u_scale;
void main() {
// Scale the positon
vec2 scaledPosition = a_position * u_scale;
// Rotate the position
vec2 rotatedPosition = vec2(
scaledPosition.x * u_rotation.y + scaledPosition.y * u_rotation.x,
scaledPosition.y * u_rotation.y - scaledPosition.x * u_rotation.x);
// Add in the translation.
vec2 position = rotatedPosition + u_translation;
...
새로운 셰이더는 훨씬 간단합니다.
<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;
uniform vec2 u_resolution;
uniform mat3 u_matrix;
void main() {
// Multiply the position by the matrix.
vec2 position = (u_matrix * vec3(a_position, 1)).xy;
...
YouTube에서 이 기능을 사용하는 방법은 다음과 같습니다.
// Draw the scene.
function drawScene() {
// Clear the canvas.
gl.clear(gl.COLOR_BUFFER_BIT);
// Compute the matrices
var translationMatrix =
makeTranslation(translation[0], translation[1]);
var rotationMatrix = makeRotation(angleInRadians);
var scaleMatrix = makeScale(scale[0], scale[1]);
// Multiply the matrices.
var matrix = matrixMultiply(scaleMatrix, rotationMatrix);
matrix = matrixMultiply(matrix, translationMatrix);
// Set the matrix.
gl.uniformMatrix3fv(matrixLocation, false, matrix);
// Draw the rectangle.
gl.drawArrays(gl.TRIANGLES, 0, 18);
}
그래도 궁금하실 수 있습니다. 큰 이점이 없는 것 같습니다 . 하지만 이제 순서를 변경하려면 새 셰이더를 작성할 필요가 없습니다. 계산을 변경하면 됩니다.
...
// Multiply the matrices.
var matrix = matrixMultiply(translationMatrix, rotationMatrix);
matrix = matrixMultiply(matrix, scaleMatrix);
...
이와 같이 행렬을 적용할 수 있는 기능은 신체의 팔, 태양 주위를 공전하는 행성의 달, 나무의 가지와 같은 계층적 애니메이션에 특히 중요합니다. 계층적 애니메이션의 간단한 예로 'F'를 5번 그려 보겠습니다. 하지만 매번 이전 'F'의 행렬부터 시작해 보겠습니다.
// Draw the scene.
function drawScene() {
// Clear the canvas.
gl.clear(gl.COLOR_BUFFER_BIT);
// Compute the matrices
var translationMatrix = makeTranslation(translation[0], translation[1]);
var rotationMatrix = makeRotation(angleInRadians);
var scaleMatrix = makeScale(scale[0], scale[1]);
// Starting Matrix.
var matrix = makeIdentity();
for (var i = 0; i < 5; ++i) {
// Multiply the matrices.
matrix = matrixMultiply(matrix, scaleMatrix);
matrix = matrixMultiply(matrix, rotationMatrix);
matrix = matrixMultiply(matrix, translationMatrix);
// Set the matrix.
gl.uniformMatrix3fv(matrixLocation, false, matrix);
// Draw the geometry.
gl.drawArrays(gl.TRIANGLES, 0, 18);
}
}
이를 위해 단위 행렬을 만드는 makeIdentity 함수를 도입했습니다. 항등 행렬은 사실상 1.0을 나타내는 행렬이므로 항등 행렬에 곱해도 아무 일도 일어나지 않습니다. 다음과 같이
X * 1 = X
so too
matrixX * identity = matrixX
다음은 정체성 행렬을 만드는 코드입니다.
function makeIdentity() {
return [
1, 0, 0,
0, 1, 0,
0, 0, 1
];
}
한 가지 예를 더 들어보겠습니다. 지금까지 모든 샘플에서 'F'는 왼쪽 상단 모서리를 중심으로 회전합니다. 이는 사용 중인 수학이 항상 원점을 중심으로 회전하고 'F'의 왼쪽 상단이 원점(0, 0)에 있기 때문입니다. 하지만 이제 행렬 수학을 실행하고 변환이 적용되는 순서를 선택할 수 있으므로 나머지 변환이 적용되기 전에 원점을 이동할 수 있습니다.
// make a matrix that will move the origin of the 'F' to
// its center.
var moveOriginMatrix = makeTranslation(-50, -75);
...
// Multiply the matrices.
var matrix = matrixMultiply(moveOriginMatrix, scaleMatrix);
matrix = matrixMultiply(matrix, rotationMatrix);
matrix = matrixMultiply(matrix, translationMatrix);
이 기법을 사용하면 어느 지점에서나 회전하거나 크기를 조절할 수 있습니다. 이제 Photoshop 또는 Flash에서 회전 지점을 이동하는 방법을 알게 되었습니다. 더 과감하게 해 보겠습니다. WebGL 기초에 관한 첫 번째 도움말로 돌아가면 셰이더에 다음과 같이 픽셀에서 클립 공간으로 변환하는 코드가 있습니다.
...
// convert the rectangle from pixels to 0.0 to 1.0
vec2 zeroToOne = position / u_resolution;
// convert from 0->1 to 0->2
vec2 zeroToTwo = zeroToOne * 2.0;
// convert from 0->2 to -1->+1 (clipspace)
vec2 clipSpace = zeroToTwo - 1.0;
gl_Position = vec4(clipSpace * vec2(1, -1), 0, 1);
각 단계를 차례로 살펴보면 첫 번째 단계인 '픽셀에서 0.0~1.0으로 변환'은 실제로 크기 조정 작업입니다. 두 번째 작업도 크기 조정 작업입니다. 다음은 변환이고 마지막은 Y를 -1로 배율 조정합니다. 실제로 셰이더에 전달하는 매트릭스에서 이 작업을 모두 실행할 수 있습니다. 1.0/해상도로 크기를 조절하는 크기 매트릭스 1개, 2.0으로 크기를 조절하는 크기 매트릭스 1개, -1.0, -1.0으로 변환하는 크기 매트릭스 1개, Y를 -1로 크기 조절하는 크기 매트릭스 1개를 만든 다음 모두 곱할 수 있지만, 수학이 간단하므로 주어진 해상도의 '투영' 매트릭스를 직접 만드는 함수를 만들겠습니다.
function make2DProjection(width, height) {
// Note: This matrix flips the Y axis so that 0 is at the top.
return [
2 / width, 0, 0,
0, -2 / height, 0,
-1, 1, 1
];
}
이제 셰이더를 더 간소화할 수 있습니다. 다음은 전체 새 정점 셰이더입니다.
<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;
uniform mat3 u_matrix;
void main() {
// Multiply the position by the matrix.
gl_Position = vec4((u_matrix * vec3(a_position, 1)).xy, 0, 1);
}
</script>
JavaScript에서는 투영 행렬을 곱해야 합니다.
// Draw the scene.
function drawScene() {
...
// Compute the matrices
var projectionMatrix =
make2DProjection(canvas.width, canvas.height);
...
// Multiply the matrices.
var matrix = matrixMultiply(scaleMatrix, rotationMatrix);
matrix = matrixMultiply(matrix, translationMatrix);
matrix = matrixMultiply(matrix, projectionMatrix);
...
}
해상도를 설정하는 코드도 삭제했습니다. 이 마지막 단계에서 행렬 수학의 마법으로 6~7단계의 다소 복잡한 셰이더에서 1단계의 매우 간단한 셰이더로 전환했습니다.
이 도움말이 행렬 수학을 이해하는 데 도움이 되었기를 바랍니다. 다음으로 3D로 넘어가겠습니다. 3D 행렬 수학은 동일한 원칙과 사용법을 따릅니다. 이해하기 쉽게 2D로 시작했습니다.

