Traduction 2D WebGL
Avant de passer à la 3D, restons encore un peu en 2D. Veuillez patienter. Cet article peut sembler extrêmement évident pour certains, mais je vais développer mon propos dans quelques articles.
Cet article fait suite à une série qui commence par Principes de base de WebGL. Si vous ne l'avez pas lu, nous vous suggérons de lire au moins le premier chapitre, puis de revenir ici. La traduction est un nom mathématique sophistiqué qui signifie essentiellement "déplacer" quelque chose. Je suppose que le déplacement d'une phrase de l'anglais vers le japonais convient également, mais dans ce cas, nous parlons de géométrie mobile. Avec l'exemple de code que nous avons obtenu dans le premier post, vous pouvez facilement traduire notre rectangle en modifiant simplement les valeurs transmises à setRectangle, n'est-ce pas ? Voici un exemple basé sur notre exemple précédent.
// First lets make some variables
// to hold the translation of the rectangle
var translation = [0, 0];
// then let's make a function to
// re-draw everything. We can call this
// function after we update the translation.
// Draw the scene.
function drawScene() {
// Clear the canvas.
gl.clear(gl.COLOR_BUFFER_BIT);
// Setup a rectangle
setRectangle(gl, translation[0], translation[1], width, height);
// Draw the rectangle.
gl.drawArrays(gl.TRIANGLES, 0, 6);
}
Pour l'instant, tout va bien. Imaginons maintenant que nous souhaitions faire la même chose avec une forme plus complexe. Imaginons que nous souhaitions dessiner un "F" composé de six triangles comme ceci.

Voici le code actuel. Nous devons remplacer setRectangle par quelque chose de plus proche de ceci.
// Fill the buffer with the values that define a letter 'F'.
function setGeometry(gl, x, y) {
var width = 100;
var height = 150;
var thickness = 30;
gl.bufferData(
gl.ARRAY_BUFFER,
new Float32Array([
// left column
x, y,
x + thickness, y,
x, y + height,
x, y + height,
x + thickness, y,
x + thickness, y + height,
// top rung
x + thickness, y,
x + width, y,
x + thickness, y + thickness,
x + thickness, y + thickness,
x + width, y,
x + width, y + thickness,
// middle rung
x + thickness, y + thickness * 2,
x + width * 2 / 3, y + thickness * 2,
x + thickness, y + thickness * 3,
x + thickness, y + thickness * 3,
x + width * 2 / 3, y + thickness * 2,
x + width * 2 / 3, y + thickness * 3]),
gl.STATIC_DRAW);
}
Vous pouvez constater que ce n'est pas une solution évolutive. Si nous voulons dessiner une géométrie très complexe avec des centaines ou des milliers de lignes, nous devrons écrire du code assez complexe. De plus, chaque fois que nous dessinons, JavaScript doit mettre à jour tous les points. Il existe une méthode plus simple. Il vous suffit d'importer la géométrie et d'effectuer la traduction dans le nuanceur. Voici le nouveau nuanceur
<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;
uniform vec2 u_resolution;
uniform vec2 u_translation;
void main() {
// Add in the translation.
vec2 position = a_position + u_translation;
// convert the rectangle from pixels to 0.0 to 1.0
vec2 zeroToOne = position / u_resolution;
...
Nous allons restructurer un peu le code. D'une part, nous n'avons besoin de définir la géométrie qu'une seule fois.
// Fill the buffer with the values that define a letter 'F'.
function setGeometry(gl) {
gl.bufferData(
gl.ARRAY_BUFFER,
new Float32Array([
// left column
0, 0,
30, 0,
0, 150,
0, 150,
30, 0,
30, 150,
// top rung
30, 0,
100, 0,
30, 30,
30, 30,
100, 0,
100, 30,
// middle rung
30, 60,
67, 60,
30, 90,
30, 90,
67, 60,
67, 90]),
gl.STATIC_DRAW);
}
Il nous suffit ensuite de mettre à jour u_translation avant de dessiner avec la traduction souhaitée.
...
var translationLocation = gl.getUniformLocation(
program, "u_translation");
...
// Set Geometry.
setGeometry(gl);
..
// Draw scene.
function drawScene() {
// Clear the canvas.
gl.clear(gl.COLOR_BUFFER_BIT);
// Set the translation.
gl.uniform2fv(translationLocation, translation);
// Draw the rectangle.
gl.drawArrays(gl.TRIANGLES, 0, 18);
}
Notez que setGeometry n'est appelé qu'une seule fois. Il n'est plus dans drawScene.
Désormais, lorsque nous dessinons, WebGL effectue pratiquement tout. Nous ne faisons que définir une traduction et lui demander de dessiner. Même si notre géométrie comportait des dizaines de milliers de points, le code principal resterait le même.
Rotation WebGL en 2D
Je vais vous avouer tout de suite que je ne sais pas si ma façon d'expliquer cela aura du sens, mais je vais quand même essayer.
Je vais d'abord vous présenter ce que l'on appelle un "cercle unité". Si vous vous souvenez de vos cours de mathématiques au collège (ne vous endormez pas !), un cercle a un rayon. Le rayon d'un cercle correspond à la distance entre le centre du cercle et le bord. Un cercle unitaire est un cercle dont le rayon est de 1,0.
Si vous vous souvenez des bases de mathématiques de la troisième année, vous savez que multiplier un nombre par 1 ne change rien. Donc 123 * 1 = 123. Plutôt basique, non ? Un cercle d'unité, c'est-à-dire un cercle dont le rayon est de 1, est également une forme de 1. Il s'agit d'un "1" en rotation. Vous pouvez donc multiplier un nombre par ce cercle d'unité. D'une certaine manière, c'est comme multiplier par 1, sauf que la magie opère et que les choses tournent. Nous allons prendre ces valeurs X et Y à partir de n'importe quel point du cercle unité, et les multiplier par notre géométrie issue de notre exemple précédent. Voici les modifications apportées à notre nuanceur.
<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;
uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;
void main() {
// Rotate the position
vec2 rotatedPosition = vec2(
a_position.x * u_rotation.y + a_position.y * u_rotation.x,
a_position.y * u_rotation.y - a_position.x * u_rotation.x);
// Add in the translation.
vec2 position = rotatedPosition + u_translation;
Nous mettons à jour le code JavaScript afin de pouvoir transmettre ces deux valeurs.
...
var rotationLocation = gl.getUniformLocation(program, "u_rotation");
...
var rotation = [0, 1];
..
// Draw the scene.
function drawScene() {
// Clear the canvas.
gl.clear(gl.COLOR_BUFFER_BIT);
// Set the translation.
gl.uniform2fv(translationLocation, translation);
// Set the rotation.
gl.uniform2fv(rotationLocation, rotation);
// Draw the rectangle.
gl.drawArrays(gl.TRIANGLES, 0, 18);
}
Pourquoi cela fonctionne-t-il ? Eh bien, regardons les calculs.
rotatedX = a_position.x * u_rotation.y + a_position.y * u_rotation.x;
rotatedY = a_position.y * u_rotation.y - a_position.x * u_rotation.x;
Supposons que vous ayez un rectangle et que vous souhaitiez le faire pivoter. Avant de commencer à la faire pivoter, elle se trouve en haut à droite, à 3,0 et 9,0. Choisissons un point sur le cercle unité à 30 degrés dans le sens des aiguilles d'une montre à partir de 12 heures.
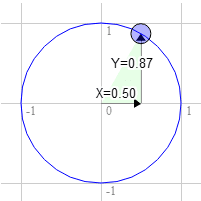
La position sur le cercle est de 0,50 et 0,87.
3.0 * 0.87 + 9.0 * 0.50 = 7.1
9.0 * 0.87 - 3.0 * 0.50 = 6.3
C'est exactement ce dont nous avons besoin

Il en va de même pour 60 degrés dans le sens des aiguilles d'une montre.
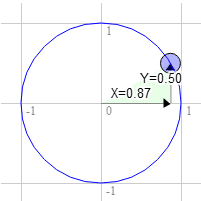
La position sur le cercle est 0,87 et 0,50.
3.0 * 0.50 + 9.0 * 0.87 = 9.3
9.0 * 0.50 - 3.0 * 0.87 = 1.9
Vous pouvez voir que lorsque nous faisons pivoter ce point dans le sens des aiguilles d'une montre, la valeur X augmente et la valeur Y diminue. Si vous continuez au-delà de 90 degrés, X commencera à diminuer à nouveau et Y à augmenter. Ce modèle permet la rotation. Les points d'un cercle unité ont un autre nom. On les appelle le sinus et le cosinus. Ainsi, pour un angle donné, nous pouvons simplement rechercher le sinus et le cosinus comme ceci.
function printSineAndCosineForAnAngle(angleInDegrees) {
var angleInRadians = angleInDegrees * Math.PI / 180;
var s = Math.sin(angleInRadians);
var c = Math.cos(angleInRadians);
console.log("s = " + s + " c = " + c);
}
Si vous copiez et collez le code dans votre console JavaScript, puis saisissez printSineAndCosignForAngle(30), vous verrez qu's = 0.49 c= 0.87 s'affiche (remarque: j'ai arrondi les nombres).
Si vous combinez tout cela, vous pouvez faire pivoter votre géométrie à l'angle de votre choix. Il vous suffit de définir la rotation sur le sinus et le cosinus de l'angle souhaité.
...
var angleInRadians = angleInDegrees * Math.PI / 180;
rotation[0] = Math.sin(angleInRadians);
rotation[1] = Math.cos(angleInRadians);
J'espère que ces informations vous ont été utiles. Voici une question plus simple. Évoluez.
Que sont les radians ?
Les radians sont une unité de mesure utilisée avec les cercles, la rotation et les angles. Tout comme nous pouvons mesurer la distance en pouces, en yards, en mètres, etc., nous pouvons mesurer les angles en degrés ou en radians.
Vous savez probablement que les calculs avec les mesures métriques sont plus faciles que ceux avec les mesures impériales. Pour convertir des pouces en pieds, divisez par 12. Pour convertir des pouces en verges, nous divisons par 36. Je ne sais pas pour vous, mais je ne peux pas diviser par 36 de tête. Avec le système métrique, c'est beaucoup plus facile. Pour passer des millimètres aux centimètres, nous divisons par 10. Pour convertir des millimètres en mètres, nous divisons par 1 000. Je peux diviser par 1 000 dans ma tête.
Les radians et les degrés sont similaires. Les degrés rendent les calculs difficiles. Les radians facilitent les calculs. Un cercle contient 360 degrés, mais seulement 2π radians. Un tour complet correspond donc à 2π radians. Un demi-tour correspond à π radians. Un quart de tour, soit 90 degrés, correspond à π/2 radians. Si vous souhaitez faire pivoter un élément de 90 degrés, utilisez simplement Math.PI * 0.5. Si vous souhaitez le faire pivoter de 45 degrés, utilisez Math.PI * 0.25, etc.
Presque tous les calculs impliquant des angles, des cercles ou des rotations fonctionnent très simplement si vous commencez à penser en radians. Alors essayez. Utilisez des radians, et non des degrés, sauf dans les affichages de l'interface utilisateur.
Échelle 2D WebGL
La mise à l'échelle est aussi simple que la traduction.
Nous multiplions la position par l'échelle souhaitée. Voici les modifications apportées à notre exemple précédent.
<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;
uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;
uniform vec2 u_scale;
void main() {
// Scale the positon
vec2 scaledPosition = a_position * u_scale;
// Rotate the position
vec2 rotatedPosition = vec2(
scaledPosition.x * u_rotation.y +
scaledPosition.y * u_rotation.x,
scaledPosition.y * u_rotation.y -
scaledPosition.x * u_rotation.x);
// Add in the translation.
vec2 position = rotatedPosition + u_translation;
Nous ajoutons le code JavaScript nécessaire pour définir l'échelle lorsque nous dessinons.
...
var scaleLocation = gl.getUniformLocation(program, "u_scale");
...
var scale = [1, 1];
...
// Draw the scene.
function drawScene() {
// Clear the canvas.
gl.clear(gl.COLOR_BUFFER_BIT);
// Set the translation.
gl.uniform2fv(translationLocation, translation);
// Set the rotation.
gl.uniform2fv(rotationLocation, rotation);
// Set the scale.
gl.uniform2fv(scaleLocation, scale);
// Draw the rectangle.
gl.drawArrays(gl.TRIANGLES, 0, 18);
}
Notez que la mise à l'échelle avec une valeur négative inverse notre géométrie. J'espère que ces trois derniers chapitres vous ont aidé à comprendre la translation, la rotation et la mise à l'échelle. Nous allons ensuite découvrir la magie des matrices, qui combinent ces trois éléments sous une forme beaucoup plus simple et souvent plus utile.
Pourquoi un "F" ?
La première fois que j'ai vu quelqu'un utiliser un "F", c'était sur une texture. La lettre "F" elle-même n'est pas importante. L'important est que vous puissiez déterminer son orientation depuis n'importe quelle direction. Si nous utilisons un cœur ♥ ou un triangle △, par exemple, nous ne pouvons pas savoir s'il a été inversé horizontalement. Un cercle ○ serait encore pire. Un rectangle coloré avec des couleurs différentes à chaque coin pourrait fonctionner, mais vous devriez vous souvenir de chaque coin. L'orientation d'un F est immédiatement reconnaissable.

N'importe quelle forme dont vous pouvez déterminer l'orientation peut fonctionner. Je n'ai utilisé que la forme "F" depuis que j'ai découvert cette idée.
Matrices 2D WebGL
Dans les trois derniers chapitres, nous avons vu comment traduire, faire pivoter et mettre à l'échelle des éléments géométriques. La translation, la rotation et l'échelle sont chacune considérées comme un type de "transformation". Chacune de ces transformations nécessitait des modifications du nuanceur, et chacune des trois transformations était dépendante de l'ordre.
Voici un exemple d'échelle de 2, 1, de rotation de 30 % et de translation de 100, 0.

Voici une translation de 100,0, une rotation de 30% et une échelle de 2, 1.

Les résultats sont complètement différents. Pire encore, si nous avions besoin du deuxième exemple, nous aurions dû écrire un autre nuanceur qui appliquerait la translation, la rotation et la mise à l'échelle dans l'ordre souhaité. Des personnes bien plus intelligentes que moi ont découvert que vous pouvez faire tout cela avec les mathématiques matricielles. Pour les images 2D, nous utilisons une matrice 3 x 3. Une matrice 3 x 3 est comme une grille de neuf cases.
| 1.0 | 2.0 | 3,0 |
| 4.0 | 5.0 | 6.0 |
| 7.0 | 8.0 | 9 |
Pour effectuer le calcul, nous multiplions la position dans les colonnes de la matrice et additionnons les résultats. Nos positions n'ont que deux valeurs, x et y, mais pour effectuer ce calcul, nous avons besoin de trois valeurs. Nous utiliserons donc 1 pour la troisième valeur. Dans ce cas, notre résultat sera
newX = x * 1.0 + y * 4.0 + 1 * 7.0
newY = x * 2.0 + y * 5.0 + 1 * 8.0
extra = x * 3.0 + y * 6.0 + 1 * 9.0
Vous vous demandez probablement "À QUOI ÇA SERT ?". Supposons que nous disposions d'une traduction. Nous appellerons le montant que nous voulons traduire tx et ty. Créons une matrice comme celle-ci
| 1.0 | 0,0 | 0.0 |
| 0,0 | 1,0 | 0,0 |
| tx | ty | 1.0 |
Et maintenant, regardez-la
newX = x * 1.0 + y * 0.0 + 1 * tx
newY = x * 0.0 + y * 1.0 + 1 * ty
extra = x * 0.0 + y * 0.0 + 1 * 1
Si vous vous souvenez de vos cours d'algèbre, vous pouvez supprimer toute décimale qui se multiplie par zéro. La multiplication par 1 ne change rien. Voyons ce qui se passe.
newX = x + tx;
newY = y + ty;
Et des éléments supplémentaires qui ne nous intéressent pas vraiment. Ce code ressemble étonnamment au code de traduction de notre exemple de traduction. De même, effectuons une rotation. Comme indiqué dans l'article sur la rotation, il nous suffit de connaître le sinus et le cosinus de l'angle de rotation souhaité.
s = Math.sin(angleToRotateInRadians);
c = Math.cos(angleToRotateInRadians);
Nous créons une matrice comme celle-ci.
| c | -s | 0,0 |
| s | c | 0,0 |
| 0.0 | 0,0 | 1.0 |
En appliquant la matrice, nous obtenons ceci :
newX = x * c + y * s + 1 * 0
newY = x * -s + y * c + 1 * 0
extra = x * 0.0 + y * 0.0 + 1 * 1
En masquant toutes les multiplications par des 0 et des 1, nous obtenons
newX = x * c + y * s;
newY = x * -s + y * c;
C'est exactement ce que nous avions dans notre exemple de rotation. Et enfin, l'évolutivité. Nous appellerons nos deux facteurs d'échelle sx et sy. Nous allons créer une matrice comme celle-ci :
| sx | 0,0 | 0.0 |
| 0,0 | sy | 0,0 |
| 0.0 | 0,0 | 1.0 |
En appliquant la matrice, nous obtenons ceci :
newX = x * sx + y * 0 + 1 * 0
newY = x * 0 + y * sy + 1 * 0
extra = x * 0.0 + y * 0.0 + 1 * 1
ce qui est vraiment
newX = x * sx;
newY = y * sy;
Ce qui est identique à notre exemple de mise à l'échelle.
Vous vous demandez peut-être : Quel en est l'intérêt ? Vous comprenez, vous ? Cela semble beaucoup de travail juste pour faire la même chose que nous faisions déjà.
C'est là que la magie opère. Il s'avère que nous pouvons multiplier des matrices et appliquer toutes les transformations en même temps. Supposons que nous ayons une fonction, matrixMultiply, qui reçoit deux matrices, les multiplie et renvoie le résultat.
Pour clarifier les choses, créons des fonctions pour créer des matrices de translation, de rotation et de mise à l'échelle.
function makeTranslation(tx, ty) {
return [
1, 0, 0,
0, 1, 0,
tx, ty, 1
];
}
function makeRotation(angleInRadians) {
var c = Math.cos(angleInRadians);
var s = Math.sin(angleInRadians);
return [
c,-s, 0,
s, c, 0,
0, 0, 1
];
}
function makeScale(sx, sy) {
return [
sx, 0, 0,
0, sy, 0,
0, 0, 1
];
}
Modifions maintenant notre nuanceur. L'ancien nuanceur se présentait comme suit :
<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;
uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;
uniform vec2 u_scale;
void main() {
// Scale the positon
vec2 scaledPosition = a_position * u_scale;
// Rotate the position
vec2 rotatedPosition = vec2(
scaledPosition.x * u_rotation.y + scaledPosition.y * u_rotation.x,
scaledPosition.y * u_rotation.y - scaledPosition.x * u_rotation.x);
// Add in the translation.
vec2 position = rotatedPosition + u_translation;
...
Notre nouveau nuanceur sera beaucoup plus simple.
<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;
uniform vec2 u_resolution;
uniform mat3 u_matrix;
void main() {
// Multiply the position by the matrix.
vec2 position = (u_matrix * vec3(a_position, 1)).xy;
...
Voici comment nous l'utilisons
// Draw the scene.
function drawScene() {
// Clear the canvas.
gl.clear(gl.COLOR_BUFFER_BIT);
// Compute the matrices
var translationMatrix =
makeTranslation(translation[0], translation[1]);
var rotationMatrix = makeRotation(angleInRadians);
var scaleMatrix = makeScale(scale[0], scale[1]);
// Multiply the matrices.
var matrix = matrixMultiply(scaleMatrix, rotationMatrix);
matrix = matrixMultiply(matrix, translationMatrix);
// Set the matrix.
gl.uniformMatrix3fv(matrixLocation, false, matrix);
// Draw the rectangle.
gl.drawArrays(gl.TRIANGLES, 0, 18);
}
Vous vous demandez peut-être : "Et alors ?". Cela ne semble pas être un avantage très intéressant . Mais maintenant, si nous voulons modifier l'ordre, nous n'avons pas besoin d'écrire un nouveau nuanceur. Nous pouvons simplement modifier les calculs.
...
// Multiply the matrices.
var matrix = matrixMultiply(translationMatrix, rotationMatrix);
matrix = matrixMultiply(matrix, scaleMatrix);
...
La possibilité d'appliquer des matrices comme celle-ci est particulièrement importante pour les animations hiérarchiques, comme les bras d'un corps, les lunes d'une planète autour d'un soleil ou les branches d'un arbre. Pour un exemple simple d'animation hiérarchique, dessinons notre "F" cinq fois, mais commençons chaque fois par la matrice de l'"F" précédent.
// Draw the scene.
function drawScene() {
// Clear the canvas.
gl.clear(gl.COLOR_BUFFER_BIT);
// Compute the matrices
var translationMatrix = makeTranslation(translation[0], translation[1]);
var rotationMatrix = makeRotation(angleInRadians);
var scaleMatrix = makeScale(scale[0], scale[1]);
// Starting Matrix.
var matrix = makeIdentity();
for (var i = 0; i < 5; ++i) {
// Multiply the matrices.
matrix = matrixMultiply(matrix, scaleMatrix);
matrix = matrixMultiply(matrix, rotationMatrix);
matrix = matrixMultiply(matrix, translationMatrix);
// Set the matrix.
gl.uniformMatrix3fv(matrixLocation, false, matrix);
// Draw the geometry.
gl.drawArrays(gl.TRIANGLES, 0, 18);
}
}
Pour ce faire, nous avons introduit la fonction makeIdentity, qui crée une matrice d'identité. Une matrice identité est une matrice qui représente effectivement 1,0.Si vous la multipliez par l'identité, rien ne se passe. Tout comme
X * 1 = X
et moi aussi
matrixX * identity = matrixX
Voici le code permettant de créer une matrice d'identité.
function makeIdentity() {
return [
1, 0, 0,
0, 1, 0,
0, 0, 1
];
}
Autre exemple : dans tous les exemples précédents, la lettre "F" pivote autour de son coin supérieur gauche. En effet, les calculs que nous utilisons pivotent toujours autour de l'origine, et l'angle supérieur gauche de notre "F" se trouve à l'origine, à l'origine (0, 0). Mais maintenant, comme nous pouvons effectuer des calculs matriciels et choisir l'ordre d'application des transformations, nous pouvons déplacer l'origine avant que le reste des transformations ne soit appliqué.
// make a matrix that will move the origin of the 'F' to
// its center.
var moveOriginMatrix = makeTranslation(-50, -75);
...
// Multiply the matrices.
var matrix = matrixMultiply(moveOriginMatrix, scaleMatrix);
matrix = matrixMultiply(matrix, rotationMatrix);
matrix = matrixMultiply(matrix, translationMatrix);
Cette technique vous permet de faire pivoter ou de mettre à l'échelle à partir de n'importe quel point. Vous savez maintenant comment déplacer le point de rotation dans Photoshop ou Flash. Allons encore plus loin. Si vous revenez au premier article sur les principes de base de WebGL, vous vous souviendrez peut-être que le code du nuanceur pour convertir les pixels en espace de découpe se présente comme suit.
...
// convert the rectangle from pixels to 0.0 to 1.0
vec2 zeroToOne = position / u_resolution;
// convert from 0->1 to 0->2
vec2 zeroToTwo = zeroToOne * 2.0;
// convert from 0->2 to -1->+1 (clipspace)
vec2 clipSpace = zeroToTwo - 1.0;
gl_Position = vec4(clipSpace * vec2(1, -1), 0, 1);
Si vous examinez chacune de ces étapes, la première, "Convertir de pixels en valeurs de 0,0 à 1,0", est en réalité une opération de mise à l'échelle. La seconde est également une opération de mise à l'échelle. La suivante est une translation, et la dernière applique une échelle de -1 à la valeur Y. Nous pouvons tout faire dans la matrice que nous transmettons au nuanceur. Nous pourrions créer deux matrices de mise à l'échelle, l'une pour la mise à l'échelle de 1,0/résolution, l'autre pour la mise à l'échelle de 2,0, une troisième pour la translation de -1,0,-1,0 et une quatrième pour la mise à l'échelle de Y de -1, puis les multiplier toutes ensemble. Mais, comme les calculs sont simples, nous allons simplement créer une fonction qui crée directement une matrice de "projection" pour une résolution donnée.
function make2DProjection(width, height) {
// Note: This matrix flips the Y axis so that 0 is at the top.
return [
2 / width, 0, 0,
0, -2 / height, 0,
-1, 1, 1
];
}
Nous pouvons maintenant simplifier encore plus le nuanceur. Voici l'intégralité du nouveau nuanceur de sommet.
<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;
uniform mat3 u_matrix;
void main() {
// Multiply the position by the matrix.
gl_Position = vec4((u_matrix * vec3(a_position, 1)).xy, 0, 1);
}
</script>
En JavaScript, nous devons multiplier par la matrice de projection
// Draw the scene.
function drawScene() {
...
// Compute the matrices
var projectionMatrix =
make2DProjection(canvas.width, canvas.height);
...
// Multiply the matrices.
var matrix = matrixMultiply(scaleMatrix, rotationMatrix);
matrix = matrixMultiply(matrix, translationMatrix);
matrix = matrixMultiply(matrix, projectionMatrix);
...
}
Nous avons également supprimé le code qui définissait la résolution. Avec cette dernière étape, nous sommes passés d'un nuanceur plutôt complexe avec six à sept étapes à un nuanceur très simple avec une seule étape, grâce à la magie des mathématiques matricielles.
J'espère que cet article vous a permis de démystifier les mathématiques matricielles. Je vais passer à la 3D. En 3D, les mathématiques matricielles suivent les mêmes principes et usages. J'ai commencé par la 2D pour que ce soit plus facile à comprendre.

