WebGL 2D 转换
在继续介绍 3D 之前,我们先继续探讨一下 2D 图形。请稍等片刻。本文对某些人来说可能显而易见,但我会在几篇文章中逐步阐述。
本文是从 WebGL 基础知识开始的系列文章的后续内容。如果您尚未阅读,建议您至少阅读第一章,然后再返回此处。 转换是一些花哨的数学术语,其基本含义是“移动”某物。我认为将句子从英语翻译成日语也是适用的,但在本例中,我们讨论的是移动几何图形。使用我们在第一篇博文中最后得到的示例代码,您只需更改传递给 setRectangle 的值,就可以轻松平移矩形,对吗?下面是一个基于上一个示例的示例。
// First lets make some variables
// to hold the translation of the rectangle
var translation = [0, 0];
// then let's make a function to
// re-draw everything. We can call this
// function after we update the translation.
// Draw the scene.
function drawScene() {
// Clear the canvas.
gl.clear(gl.COLOR_BUFFER_BIT);
// Setup a rectangle
setRectangle(gl, translation[0], translation[1], width, height);
// Draw the rectangle.
gl.drawArrays(gl.TRIANGLES, 0, 6);
}
目前为止,一切顺利。现在假设我们想使用更复杂的形状来执行相同的操作。假设我们想绘制一个由 6 个三角形组成的“F”,如下所示。

下面是当前的代码,我们必须将 setRectangle 更改为类似于以下内容的代码。
// Fill the buffer with the values that define a letter 'F'.
function setGeometry(gl, x, y) {
var width = 100;
var height = 150;
var thickness = 30;
gl.bufferData(
gl.ARRAY_BUFFER,
new Float32Array([
// left column
x, y,
x + thickness, y,
x, y + height,
x, y + height,
x + thickness, y,
x + thickness, y + height,
// top rung
x + thickness, y,
x + width, y,
x + thickness, y + thickness,
x + thickness, y + thickness,
x + width, y,
x + width, y + thickness,
// middle rung
x + thickness, y + thickness * 2,
x + width * 2 / 3, y + thickness * 2,
x + thickness, y + thickness * 3,
x + thickness, y + thickness * 3,
x + width * 2 / 3, y + thickness * 2,
x + width * 2 / 3, y + thickness * 3]),
gl.STATIC_DRAW);
}
希望您能明白,这样做无法很好地扩展。如果我们想绘制包含数百或数千行代码的非常复杂的几何图形,就必须编写一些非常复杂的代码。此外,每次绘制时,JavaScript 都必须更新所有点。其实还有更简单的方法。只需上传几何图形并在着色器中执行转换即可。 以下是新的着色器
<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;
uniform vec2 u_resolution;
uniform vec2 u_translation;
void main() {
// Add in the translation.
vec2 position = a_position + u_translation;
// convert the rectangle from pixels to 0.0 to 1.0
vec2 zeroToOne = position / u_resolution;
...
我们稍微重构一下代码。首先,我们只需设置一次几何图形。
// Fill the buffer with the values that define a letter 'F'.
function setGeometry(gl) {
gl.bufferData(
gl.ARRAY_BUFFER,
new Float32Array([
// left column
0, 0,
30, 0,
0, 150,
0, 150,
30, 0,
30, 150,
// top rung
30, 0,
100, 0,
30, 30,
30, 30,
100, 0,
100, 30,
// middle rung
30, 60,
67, 60,
30, 90,
30, 90,
67, 60,
67, 90]),
gl.STATIC_DRAW);
}
然后,我们只需更新 u_translation,然后即可使用所需的平移进行绘制。
...
var translationLocation = gl.getUniformLocation(
program, "u_translation");
...
// Set Geometry.
setGeometry(gl);
..
// Draw scene.
function drawScene() {
// Clear the canvas.
gl.clear(gl.COLOR_BUFFER_BIT);
// Set the translation.
gl.uniform2fv(translationLocation, translation);
// Draw the rectangle.
gl.drawArrays(gl.TRIANGLES, 0, 18);
}
请注意,setGeometry 仅会被调用一次。它不再位于 drawScene 内。
现在,当我们绘制时,WebGL 几乎会执行所有操作。我们只需设置一个转换并让其绘制即可。即使几何图形有数万个点,主要代码也会保持不变。
WebGL 2D 旋转
我要先承认,我不知道我这样解释是否有意义,但没关系,不妨试试。
首先,我想向您介绍一下“单位圆”。如果您还记得初中数学(别睡着了!),就知道圆形有半径。圆形的半径是指从圆心到边缘的距离。单位圆是半径为 1.0 的圆。
还记得三年级数学基础知识吗?如果某个数乘以 1,则结果不变。因此,123 * 1 = 123。很简单,对吧?单位圆(半径为 1.0 的圆)也是 1 的一种形式。它是一个旋转的 1。因此,您可以将某个值乘以这个单位圆,从某种意义上讲,这有点像乘以 1,只不过会发生神奇的事情,并且内容会旋转。我们将从单位圆上的任意一点获取 X 和 Y 值,并将几何图形与上一个示例中的这些值相乘。以下是着色器的更新。
<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;
uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;
void main() {
// Rotate the position
vec2 rotatedPosition = vec2(
a_position.x * u_rotation.y + a_position.y * u_rotation.x,
a_position.y * u_rotation.y - a_position.x * u_rotation.x);
// Add in the translation.
vec2 position = rotatedPosition + u_translation;
我们更新了 JavaScript,以便传入这两个值。
...
var rotationLocation = gl.getUniformLocation(program, "u_rotation");
...
var rotation = [0, 1];
..
// Draw the scene.
function drawScene() {
// Clear the canvas.
gl.clear(gl.COLOR_BUFFER_BIT);
// Set the translation.
gl.uniform2fv(translationLocation, translation);
// Set the rotation.
gl.uniform2fv(rotationLocation, rotation);
// Draw the rectangle.
gl.drawArrays(gl.TRIANGLES, 0, 18);
}
为什么这样做?我们来看看计算结果。
rotatedX = a_position.x * u_rotation.y + a_position.y * u_rotation.x;
rotatedY = a_position.y * u_rotation.y - a_position.x * u_rotation.x;
假设您有一个矩形,并且想要旋转它。在开始旋转之前,右上角位于 3.0, 9.0。我们在单位圆上选择一个点,从 12 点顺时针旋转 30 度。
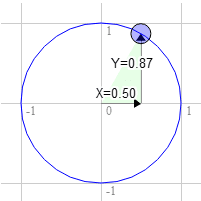
在圆形上的位置为 0.50 和 0.87
3.0 * 0.87 + 9.0 * 0.50 = 7.1
9.0 * 0.87 - 3.0 * 0.50 = 6.3
这正是我们需要的

顺时针旋转 60 度也是如此
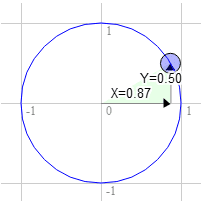
在圆形上的位置为 0.87 和 0.50
3.0 * 0.50 + 9.0 * 0.87 = 9.3
9.0 * 0.50 - 3.0 * 0.87 = 1.9
您可以看到,当我们顺时针向右旋转该点时,X 值会变大,Y 值会变小。如果继续超过 90 度,X 将再次变小,而 Y 将开始变大。这种模式会产生旋转。单位圆上的点还有一个名称。它们分别称为正弦和余弦。因此,对于任何给定的角度,我们都可以像这样查找正弦和余弦。
function printSineAndCosineForAnAngle(angleInDegrees) {
var angleInRadians = angleInDegrees * Math.PI / 180;
var s = Math.sin(angleInRadians);
var c = Math.cos(angleInRadians);
console.log("s = " + s + " c = " + c);
}
如果您将代码复制并粘贴到 JavaScript 控制台中,然后输入 printSineAndCosignForAngle(30),您会看到控制台输出 s = 0.49 c= 0.87(注意:我对数字进行了四舍五入)。将所有这些组合起来,您就可以将几何图形旋转到所需的任何角度。只需将旋转设置为要旋转到的角度的正弦和余弦即可。
...
var angleInRadians = angleInDegrees * Math.PI / 180;
rotation[0] = Math.sin(angleInRadians);
rotation[1] = Math.cos(angleInRadians);
希望以上说明对您有所帮助。接下来是一个更简单的示例。灵活扩缩。
什么是弧度?
弧度是用于圆形、旋转和角度的衡量单位。就像我们可以用英寸、码、米等单位来衡量距离一样,我们也可以用度或弧度来衡量角度。
您可能知道,使用公制单位进行计算比使用英制单位进行计算更容易。如需将英寸换算为英尺,请除以 12。如需将英寸换算为码,请除以 36。我不知道您是怎么样的,但我无法在脑子里除以 36。使用公制单位会更简单。如需将毫米换算成厘米,请除以 10。如需将毫米换算为米,请除以 1000。我可以在脑中进行除以 1000 的运算。
弧度与角度类似。使用度数会使计算变得复杂。使用弧度可以简化计算。圆形有 360 度,但只有 2π 弧度。因此,一圈是 2π 弧度。半圈是 π 弧度。1/4 圈(即 90 度)为 π/2 弧度。因此,如果您想旋转 90 度,只需使用 Math.PI * 0.5 即可。如果您想将其旋转 45 度,请使用 Math.PI * 0.25 等。
如果您开始以弧度为单位思考,几乎所有涉及角度、圆形或旋转的数学问题都会变得非常简单。因此,请试一试。除界面显示之外,请使用弧度,而不是角度。
WebGL 2D 缩放
扩展规模就像翻译一样简单。
我们将位置乘以所需的比例。下面是与上一个示例的变化。
<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;
uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;
uniform vec2 u_scale;
void main() {
// Scale the positon
vec2 scaledPosition = a_position * u_scale;
// Rotate the position
vec2 rotatedPosition = vec2(
scaledPosition.x * u_rotation.y +
scaledPosition.y * u_rotation.x,
scaledPosition.y * u_rotation.y -
scaledPosition.x * u_rotation.x);
// Add in the translation.
vec2 position = rotatedPosition + u_translation;
我们在绘制时添加了设置比例所需的 JavaScript。
...
var scaleLocation = gl.getUniformLocation(program, "u_scale");
...
var scale = [1, 1];
...
// Draw the scene.
function drawScene() {
// Clear the canvas.
gl.clear(gl.COLOR_BUFFER_BIT);
// Set the translation.
gl.uniform2fv(translationLocation, translation);
// Set the rotation.
gl.uniform2fv(rotationLocation, rotation);
// Set the scale.
gl.uniform2fv(scaleLocation, scale);
// Draw the rectangle.
gl.drawArrays(gl.TRIANGLES, 0, 18);
}
需要注意的是,按负值缩放会翻转我们的几何图形。希望前面 3 章内容对您了解平移、旋转和缩放有所帮助。接下来,我们将介绍矩阵的神奇之处,它可以将这 3 种方法组合成一种更简单、更实用的形式。
为什么是“F”?
我第一次看到有人使用“F”是在纹理上。“F”本身并不重要。重要的是,您可以从任何方向判断其方向。例如,如果我们使用的是心形 ♥ 或三角形 △,我们无法判断它是否已水平翻转。圆形 ○ 会更糟糕。可以说,使用颜色矩形,每个角的颜色可以不同,但您必须记住哪个角是哪个角。F 的方向一目了然。

只要您能看出方向的任何形状都可以,自从我第一次接触这个概念以来,我就一直使用“F”。
WebGL 2D 矩阵
在前 3 章中,我们介绍了如何平移几何图形、旋转几何图形和缩放几何图形。平移、旋转和缩放都被视为一种“转换”。每种转换都需要更改着色器,并且 3 种转换中的每种转换都依赖于顺序。
例如,下面的缩放比例为 2, 1,旋转角度为 30%,平移为 100, 0。

下面是平移为 100,0、旋转为 30% 且缩放为 2,1 的示例

结果完全不同。更糟糕的是,如果我们需要第二个示例,则必须编写其他着色器,以便按照我们新希望的顺序应用平移、旋转和缩放。不过,有些人比我聪明得多,他们发现您可以使用矩阵运算来完成所有相同的操作。对于 2d,我们使用 3x3 矩阵。3x3 矩阵就像包含 9 个方格的网格。
| 1.0 | 2.0 | 3.0 |
| 4.0 | 5.0 | 6.0 |
| 7.0 | 8.0 | 9.0 |
为了进行计算,我们将矩阵列中的相应位置相乘,然后将结果相加。我们的坐标只有 2 个值,即 x 和 y,但为了进行此计算,我们需要 3 个值,因此我们将第三个值设为 1。在本例中,结果为
newX = x * 1.0 + y * 4.0 + 1 * 7.0
newY = x * 2.0 + y * 5.0 + 1 * 8.0
extra = x * 3.0 + y * 6.0 + 1 * 9.0
您可能会看到这个问题,然后想“这有什么用?”假设我们有翻译。我们将要转换的量称为 tx 和 ty。我们来创建一个这样的矩阵
| 1.0 | 0.0 | 0.0 |
| 0.0 | 1.0 | 0.0 |
| tx | ty | 1.0 |
现在,请查看
newX = x * 1.0 + y * 0.0 + 1 * tx
newY = x * 0.0 + y * 1.0 + 1 * ty
extra = x * 0.0 + y * 0.0 + 1 * 1
如果您还记得代数学,我们可以删除任何乘以零的位置。乘以 1 实际上没有任何作用,因此我们来简化一下,看看会发生什么
newX = x + tx;
newY = y + ty;
我们不太关心额外的费用。这与我们的翻译示例中的翻译代码非常相似。同样,我们来实现旋转。正如我们在旋转博文中指出的那样,我们只需要要旋转的角度的正弦和余弦。
s = Math.sin(angleToRotateInRadians);
c = Math.cos(angleToRotateInRadians);
我们构建一个这样的矩阵
| c | -s | 0.0 |
| 秒 | c | 0.0 |
| 0.0 | 0.0 | 1.0 |
应用矩阵后,我们得到了以下结果
newX = x * c + y * s + 1 * 0
newY = x * -s + y * c + 1 * 0
extra = x * 0.0 + y * 0.0 + 1 * 1
将所有乘以 0 和 1 的项涂黑,我们得到
newX = x * c + y * s;
newY = x * -s + y * c;
这正是我们的轮替示例中所示。最后是扩展。我们将 2 个缩放比例称为 sx 和 sy,并构建如下矩阵
| sx | 0.0 | 0.0 |
| 0.0 | sy | 0.0 |
| 0.0 | 0.0 | 1.0 |
应用矩阵后,我们得到了以下结果
newX = x * sx + y * 0 + 1 * 0
newY = x * 0 + y * sy + 1 * 0
extra = x * 0.0 + y * 0.0 + 1 * 1
这实际上
newX = x * sx;
newY = y * sy;
这与我们的缩放示例相同。我知道您可能仍在思考。那又如何?有什么意义。这似乎需要做很多工作,只是为了执行我们之前在做的相同操作?这正是神奇之处。事实证明,我们可以将矩阵相乘,并一次性应用所有转换。假设我们有一个函数 matrixMultiply,它接受两个矩阵,对它们进行乘法并返回结果。为了更清楚地说明,我们来创建一些函数来构建平移、旋转和缩放的矩阵。
function makeTranslation(tx, ty) {
return [
1, 0, 0,
0, 1, 0,
tx, ty, 1
];
}
function makeRotation(angleInRadians) {
var c = Math.cos(angleInRadians);
var s = Math.sin(angleInRadians);
return [
c,-s, 0,
s, c, 0,
0, 0, 1
];
}
function makeScale(sx, sy) {
return [
sx, 0, 0,
0, sy, 0,
0, 0, 1
];
}
现在,我们来更改着色器。旧着色器如下所示
<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;
uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;
uniform vec2 u_scale;
void main() {
// Scale the positon
vec2 scaledPosition = a_position * u_scale;
// Rotate the position
vec2 rotatedPosition = vec2(
scaledPosition.x * u_rotation.y + scaledPosition.y * u_rotation.x,
scaledPosition.y * u_rotation.y - scaledPosition.x * u_rotation.x);
// Add in the translation.
vec2 position = rotatedPosition + u_translation;
...
我们的新着色器将会更加简单。
<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;
uniform vec2 u_resolution;
uniform mat3 u_matrix;
void main() {
// Multiply the position by the matrix.
vec2 position = (u_matrix * vec3(a_position, 1)).xy;
...
我们会这样使用
// Draw the scene.
function drawScene() {
// Clear the canvas.
gl.clear(gl.COLOR_BUFFER_BIT);
// Compute the matrices
var translationMatrix =
makeTranslation(translation[0], translation[1]);
var rotationMatrix = makeRotation(angleInRadians);
var scaleMatrix = makeScale(scale[0], scale[1]);
// Multiply the matrices.
var matrix = matrixMultiply(scaleMatrix, rotationMatrix);
matrix = matrixMultiply(matrix, translationMatrix);
// Set the matrix.
gl.uniformMatrix3fv(matrixLocation, false, matrix);
// Draw the rectangle.
gl.drawArrays(gl.TRIANGLES, 0, 18);
}
不过,您可能仍会问,这有什么意义?这似乎没什么好处。不过,现在如果我们想更改顺序,则无需编写新的着色器。我们可以更改计算方式。
...
// Multiply the matrices.
var matrix = matrixMultiply(translationMatrix, rotationMatrix);
matrix = matrixMultiply(matrix, scaleMatrix);
...
对于分层动画(例如身体上的手臂、围绕太阳运行的行星上的卫星或树上的树枝)来说,能够应用这样的矩阵尤为重要。下面是一个简单的分层动画示例,我们将绘制 5 次“F”,但每次都从上一个“F”的矩阵开始。
// Draw the scene.
function drawScene() {
// Clear the canvas.
gl.clear(gl.COLOR_BUFFER_BIT);
// Compute the matrices
var translationMatrix = makeTranslation(translation[0], translation[1]);
var rotationMatrix = makeRotation(angleInRadians);
var scaleMatrix = makeScale(scale[0], scale[1]);
// Starting Matrix.
var matrix = makeIdentity();
for (var i = 0; i < 5; ++i) {
// Multiply the matrices.
matrix = matrixMultiply(matrix, scaleMatrix);
matrix = matrixMultiply(matrix, rotationMatrix);
matrix = matrixMultiply(matrix, translationMatrix);
// Set the matrix.
gl.uniformMatrix3fv(matrixLocation, false, matrix);
// Draw the geometry.
gl.drawArrays(gl.TRIANGLES, 0, 18);
}
}
为此,我们引入了用于创建单位矩阵的函数 makeIdentity。单位矩阵实际上表示 1.0,因此如果您对其进行乘法,则不会发生任何变化。就像
X * 1 = X
同样
matrixX * identity = matrixX
以下是用于创建身份矩阵的代码。
function makeIdentity() {
return [
1, 0, 0,
0, 1, 0,
0, 0, 1
];
}
再举一个例子,在目前的每个示例中,我们的“F”都围绕其左上角旋转。这是因为我们使用的数学运算始终围绕原点旋转,而“F”的左上角位于原点 (0, 0)。不过现在,由于我们可以进行矩阵运算,并且可以选择应用转换的顺序,因此可以在应用其余转换之前移动原点。
// make a matrix that will move the origin of the 'F' to
// its center.
var moveOriginMatrix = makeTranslation(-50, -75);
...
// Multiply the matrices.
var matrix = matrixMultiply(moveOriginMatrix, scaleMatrix);
matrix = matrixMultiply(matrix, rotationMatrix);
matrix = matrixMultiply(matrix, translationMatrix);
使用此方法,您可以从任意位置旋转或缩放。现在,您已经了解了如何使用 Photoshop 或 Flash 移动旋转中心。 我们来玩得更疯狂一点。如果您回顾一下WebGL 基础知识的第一篇文章,可能会记得我们在着色器中添加了用于从像素转换为剪裁空间的代码,该代码如下所示。
...
// convert the rectangle from pixels to 0.0 to 1.0
vec2 zeroToOne = position / u_resolution;
// convert from 0->1 to 0->2
vec2 zeroToTwo = zeroToOne * 2.0;
// convert from 0->2 to -1->+1 (clipspace)
vec2 clipSpace = zeroToTwo - 1.0;
gl_Position = vec4(clipSpace * vec2(1, -1), 0, 1);
如果您依次查看这些步骤,就会发现第一个步骤“将像素值转换为 0.0 到 1.0”实际上是缩放操作。第二个也是缩放操作。下一个是平移,最后一个是将 Y 缩放为 -1。实际上,我们可以在传递给着色器的矩阵中完成所有这些操作。我们可以创建 2 个缩放矩阵,一个按 1.0/resolution 缩放,另一个按 2.0 缩放,第三个按 -1.0,-1.0 平移,第四个按 -1 缩放 Y,然后将它们全部相乘,但由于计算很简单,我们只需创建一个函数,直接为给定分辨率创建“投影”矩阵。
function make2DProjection(width, height) {
// Note: This matrix flips the Y axis so that 0 is at the top.
return [
2 / width, 0, 0,
0, -2 / height, 0,
-1, 1, 1
];
}
现在,我们可以进一步简化着色器。下面是完整的新顶点着色器。
<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;
uniform mat3 u_matrix;
void main() {
// Multiply the position by the matrix.
gl_Position = vec4((u_matrix * vec3(a_position, 1)).xy, 0, 1);
}
</script>
在 JavaScript 中,我们需要乘以投影矩阵
// Draw the scene.
function drawScene() {
...
// Compute the matrices
var projectionMatrix =
make2DProjection(canvas.width, canvas.height);
...
// Multiply the matrices.
var matrix = matrixMultiply(scaleMatrix, rotationMatrix);
matrix = matrixMultiply(matrix, translationMatrix);
matrix = matrixMultiply(matrix, projectionMatrix);
...
}
我们还移除了用于设置分辨率的代码。通过这最后一步,我们将包含 6-7 个步骤的相当复杂的着色器转换成了包含 1 个步骤的非常简单的着色器,这一切都得益于矩阵数学的魔力。
希望本文能帮助您解开矩阵数学的神秘面纱。接下来,我将介绍 3D 内容。在 3D 矩阵中,数学运算遵循相同的原则和用法。我先从 2D 开始,希望能让大家轻松理解。

