Diese Seite wurde von der Cloud Translation API übersetzt.

WebGL-Transformationen

Gregg Tavares

WebGL-2D-Übersetzung

Bevor wir zu 3D übergehen, bleiben wir noch etwas bei 2D. Bitte haben Sie einen Moment Geduld. Dieser Artikel mag für manche überflüssig erscheinen, aber ich werde in einigen Artikeln darauf eingehen.

Dieser Artikel ist eine Fortsetzung einer Reihe, die mit WebGL-Grundlagen beginnt. Wenn Sie es noch nicht gelesen haben, sollten Sie sich zumindest das erste Kapitel durchlesen und dann wieder hierher zurückkehren. „Translation“ ist ein komplizierter mathematischer Begriff, der im Grunde „etwas verschieben“ bedeutet. Ich nehme an, dass auch das Verschieben eines Satzes vom Englischen ins Japanische passen würde, aber in diesem Fall geht es um das Verschieben von Geometrie. Mit dem Beispielcode aus dem ersten Beitrag können Sie unser Rechteck ganz einfach verschieben, indem Sie einfach die an setRectangle übergebenen Werte ändern. Stimmt das? Hier ist ein Beispiel, das auf unserem vorherigen Beispiel basiert.

  // First lets make some variables 
  // to hold the translation of the rectangle
  var translation = [0, 0];
  // then let's make a function to
  // re-draw everything. We can call this
  // function after we update the translation.
  // Draw the scene.
  function drawScene() {
     // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);
    // Setup a rectangle
    setRectangle(gl, translation[0], translation[1], width, height);

    // Draw the rectangle.
    gl.drawArrays(gl.TRIANGLES, 0, 6);
  }

So weit, so gut. Stellen Sie sich nun vor, wir möchten dasselbe mit einer komplizierteren Form tun. Angenommen, wir möchten ein „F“ zeichnen, das aus sechs Dreiecken besteht.

Im folgenden Code müssten wir „setRectangle“ in etwa so ändern:

// Fill the buffer with the values that define a letter 'F'.
function setGeometry(gl, x, y) {
  var width = 100;
  var height = 150;
  var thickness = 30;
  gl.bufferData(
      gl.ARRAY_BUFFER,
      new Float32Array([
          // left column
          x, y,
          x + thickness, y,
          x, y + height,
          x, y + height,
          x + thickness, y,
          x + thickness, y + height,

          // top rung
          x + thickness, y,
          x + width, y,
          x + thickness, y + thickness,
          x + thickness, y + thickness,
          x + width, y,
          x + width, y + thickness,

          // middle rung
          x + thickness, y + thickness * 2,
          x + width * 2 / 3, y + thickness * 2,
          x + thickness, y + thickness * 3,
          x + thickness, y + thickness * 3,
          x + width * 2 / 3, y + thickness * 2,
          x + width * 2 / 3, y + thickness * 3]),
      gl.STATIC_DRAW);
}

Sie können sich vorstellen, dass das nicht gut skaliert. Wenn wir eine sehr komplexe Geometrie mit Hunderten oder Tausenden von Linien zeichnen möchten, müssten wir ziemlich komplexen Code schreiben. Außerdem müssen jedes Mal, wenn wir zeichnen, alle Punkte in JavaScript aktualisiert werden. Es gibt aber eine einfachere Möglichkeit. Laden Sie einfach die Geometrie hoch und führen Sie die Übersetzung im Shader aus. Hier ist der neue Shader

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform vec2 u_translation;

void main() {
   // Add in the translation.
   vec2 position = a_position + u_translation;

   // convert the rectangle from pixels to 0.0 to 1.0
   vec2 zeroToOne = position / u_resolution;
   ...

und wir strukturieren den Code ein wenig um. Zum einen müssen wir die Geometrie nur einmal festlegen.

// Fill the buffer with the values that define a letter 'F'.
function setGeometry(gl) {
  gl.bufferData(
      gl.ARRAY_BUFFER,
      new Float32Array([
          // left column
          0, 0,
          30, 0,
          0, 150,
          0, 150,
          30, 0,
          30, 150,

          // top rung
          30, 0,
          100, 0,
          30, 30,
          30, 30,
          100, 0,
          100, 30,

          // middle rung
          30, 60,
          67, 60,
          30, 90,
          30, 90,
          67, 60,
          67, 90]),
      gl.STATIC_DRAW);
}

Dann müssen wir nur noch u_translation aktualisieren, bevor wir mit der gewünschten Übersetzung zeichnen.

  ...
  var translationLocation = gl.getUniformLocation(
             program, "u_translation");
  ...
  // Set Geometry.
  setGeometry(gl);
  ..
  // Draw scene.
  function drawScene() {
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Set the translation.
    gl.uniform2fv(translationLocation, translation);

    // Draw the rectangle.
    gl.drawArrays(gl.TRIANGLES, 0, 18);
  }

Beachten Sie, dass setGeometry nur einmal aufgerufen wird. Es befindet sich nicht mehr in drawScene.

Wenn wir jetzt etwas zeichnen, übernimmt WebGL praktisch alles. Wir legen einfach eine Übersetzung fest und bitten den Algorithmus, etwas zu zeichnen. Selbst wenn unsere Geometrie Zehntausende von Punkten hätte, würde der Hauptcode unverändert bleiben.

WebGL-2D-Drehung

Ich muss gleich zugeben, dass ich keine Ahnung habe, ob meine Erklärung Sinn ergibt, aber was soll's, ich kann es ja versuchen.

Zuerst möchte ich Ihnen den sogenannten Einheitskreis vorstellen. Wenn Sie sich an die Mathematik in der Mittelschule erinnern (fallen Sie mir nicht ins Koma!), hat ein Kreis einen Radius. Der Radius eines Kreises ist der Abstand vom Mittelpunkt des Kreises zum Rand. Ein Einheitskreis ist ein Kreis mit einem Radius von 1,0.

Wie Sie aus der Mathematik der 3. Klasse wissen, bleibt ein Wert unverändert, wenn Sie ihn mit 1 multiplizieren. 123 × 1 = 123. Ganz einfach, oder? Ein Einheitskreis, also ein Kreis mit einem Radius von 1,0, ist auch eine Form der 1. Es ist eine rotierende 1. Sie können also etwas mit diesem Einheitskreis multiplizieren. Das ist in gewisser Weise mit einer Multiplikation mit 1 vergleichbar, mit dem Unterschied, dass sich die Dinge drehen. Wir nehmen diese X- und Y-Werte von einem beliebigen Punkt auf dem Einheitskreis und multiplizieren unsere Geometrie aus unserem vorherigen Beispiel damit. Hier sind die Änderungen an unserem Shader.

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;

void main() {
  // Rotate the position
  vec2 rotatedPosition = vec2(
     a_position.x * u_rotation.y + a_position.y * u_rotation.x,
     a_position.y * u_rotation.y - a_position.x * u_rotation.x);

  // Add in the translation.
  vec2 position = rotatedPosition + u_translation;

Wir aktualisieren das JavaScript, damit wir diese beiden Werte übergeben können.

  ...
  var rotationLocation = gl.getUniformLocation(program, "u_rotation");
  ...
  var rotation = [0, 1];
  ..
  // Draw the scene.
  function drawScene() {
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Set the translation.
    gl.uniform2fv(translationLocation, translation);

    // Set the rotation.
    gl.uniform2fv(rotationLocation, rotation);

    // Draw the rectangle.
    gl.drawArrays(gl.TRIANGLES, 0, 18);
  }

Warum funktioniert das? Sehen wir uns die Zahlen an.

rotatedX = a_position.x * u_rotation.y + a_position.y * u_rotation.x;
rotatedY = a_position.y * u_rotation.y - a_position.x * u_rotation.x;

Angenommen, Sie haben ein Rechteck und möchten es drehen. Bevor Sie mit der Drehung beginnen, befindet sich der rechte obere Eckpunkt bei 3.0, 9.0. Wählen wir einen Punkt auf dem Einheitskreis aus, der sich 30 Grad im Uhrzeigersinn von der 12 Uhr-Position befindet.

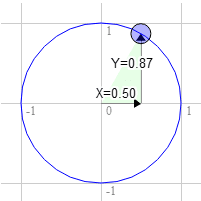
Die Position auf dem Kreis ist 0,50 und 0,87.

3.0 * 0.87 + 9.0 * 0.50 = 7.1
9.0 * 0.87 - 3.0 * 0.50 = 6.3

Genau dort müssen wir sie haben.

Dasselbe gilt für 60 Grad im Uhrzeigersinn.

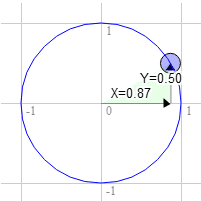
Die Position auf dem Kreis ist 0,87 und 0,50.

3.0 * 0.50 + 9.0 * 0.87 = 9.3
9.0 * 0.50 - 3.0 * 0.87 = 1.9

Sie sehen, dass der X-Wert größer und der Y-Wert kleiner wird, wenn wir den Punkt im Uhrzeigersinn nach rechts drehen. Wenn Sie weiter als 90 Grad gehen, wird X wieder kleiner und Y größer. Dieses Muster sorgt für die Drehung. Die Punkte auf einem Einheitskreis haben noch einen anderen Namen. Sie werden als Sinus und Kosinus bezeichnet. Für jeden beliebigen Winkel können wir also den Sinus und den Kosinus so nachschlagen.

function printSineAndCosineForAnAngle(angleInDegrees) {
  var angleInRadians = angleInDegrees * Math.PI / 180;
  var s = Math.sin(angleInRadians);
  var c = Math.cos(angleInRadians);
  console.log("s = " + s + " c = " + c);
}

Wenn Sie den Code in die JavaScript-Konsole kopieren und einfügen und dann printSineAndCosignForAngle(30) eingeben, wird s = 0.49 c= 0.87 ausgegeben. Hinweis: Ich habe die Zahlen gerundet. Wenn Sie alles zusammenführen, können Sie die Geometrie in beliebigen Winkeln drehen. Legen Sie dazu einfach den Sinus und den Kosinus des gewünschten Drehwinkels fest.

  ...
  var angleInRadians = angleInDegrees * Math.PI / 180;
  rotation[0] = Math.sin(angleInRadians);
  rotation[1] = Math.cos(angleInRadians);

Ich hoffe, das war verständlich. Als Nächstes eine einfachere Frage. Skalieren.

Was sind Radian?

Bogenmaße sind eine Maßeinheit, die für Kreise, Drehungen und Winkel verwendet wird. Genau wie wir Entfernungen in Zoll, Yards, Metern usw. messen können, können wir Winkel in Grad oder Bogenmaß messen.

Ihnen ist wahrscheinlich bewusst, dass Mathematik mit metrischen Maßeinheiten einfacher ist als Mathematik mit imperialen Maßeinheiten. Um von Zoll in Fuß umzurechnen, dividieren wir durch 12. Um von Zoll in Yards umzurechnen, dividieren wir durch 36. Ich weiß nicht, wie es Ihnen geht, aber ich kann nicht im Kopf durch 36 teilen. Mit dem metrischen System ist es viel einfacher. Um von Millimetern auf Zentimeter umzurechnen, teilen wir durch 10. Um von Millimetern in Meter umzurechnen, teilen wir durch 1.000. Ich kann im Kopf durch 1.000 teilen.

Radiante und Grad sind ähnlich. Grade machen die Berechnungen schwierig. Mit Radianen wird die Mathematik einfacher. Ein Kreis hat 360 Grad, aber nur 2π Radiane. Eine volle Umdrehung entspricht also 2π Radianten. Eine halbe Umdrehung entspricht π Radianten. Eine Vierteldrehung, also 90 Grad, entspricht π/2 Radian. Wenn Sie etwas um 90 Grad drehen möchten, verwenden Sie einfach Math.PI * 0.5. Wenn Sie es um 45 Grad drehen möchten, verwenden Sie Math.PI * 0.25 usw.

Fast alle mathematischen Berechnungen, die Winkel, Kreise oder Drehungen umfassen, sind sehr einfach, wenn Sie in Radianen denken. Probieren Sie es einfach aus. Verwenden Sie Radian, nicht Grad, außer in der Benutzeroberfläche.

WebGL-2D-Skalierung

Das Skalieren ist genauso einfach wie die Übersetzung.

Wir multiplizieren die Position mit dem gewünschten Maßstab. Hier sind die Änderungen aus unserem vorherigen Beispiel.

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;
uniform vec2 u_scale;

void main() {
  // Scale the positon
  vec2 scaledPosition = a_position * u_scale;

  // Rotate the position
  vec2 rotatedPosition = vec2(
     scaledPosition.x * u_rotation.y +
        scaledPosition.y * u_rotation.x,
     scaledPosition.y * u_rotation.y -
        scaledPosition.x * u_rotation.x);

  // Add in the translation.
  vec2 position = rotatedPosition + u_translation;

und wir fügen das JavaScript hinzu, das zum Festlegen des Maßstabs beim Zeichnen erforderlich ist.

  ...
  var scaleLocation = gl.getUniformLocation(program, "u_scale");
  ...
  var scale = [1, 1];
  ...
  // Draw the scene.
  function drawScene() {
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Set the translation.
    gl.uniform2fv(translationLocation, translation);

    // Set the rotation.
    gl.uniform2fv(rotationLocation, rotation);

    // Set the scale.
    gl.uniform2fv(scaleLocation, scale);

    // Draw the rectangle.
    gl.drawArrays(gl.TRIANGLES, 0, 18);
  }

Beachten Sie, dass die Geometrie durch eine Skalierung mit einem negativen Wert gespiegelt wird. Ich hoffe, dass diese letzten drei Kapitel Ihnen dabei geholfen haben, Verschiebung, Drehung und Skalierung zu verstehen. Als Nächstes sehen wir uns die Magie von Matrizen an, die alle drei in einer viel einfacheren und oft nützlicheren Form kombinieren.

Warum ein „F“?

Das erste Mal, dass ich sah, wie jemand ein „F“ verwendete, war auf einer Textur. Das „F“ selbst ist nicht wichtig. Wichtig ist, dass Sie die Ausrichtung aus jeder Richtung erkennen können. Wenn wir beispielsweise ein Herz ♥ oder ein Dreieck △ verwenden, können wir nicht erkennen, ob es horizontal gespiegelt wurde. Ein Kreis ○ wäre noch schlimmer. Ein farbiges Rechteck würde mit verschiedenen Farben an jeder Ecke funktionieren, aber dann müssten Sie sich merken, welche Ecke welche ist. Die Ausrichtung eines F ist sofort erkennbar.

Jede Form, deren Ausrichtung Sie erkennen können, würde funktionieren. Ich verwende einfach „F“, seit ich die Idee kennengelernt habe.

WebGL-2D-Matrizen

In den letzten drei Kapiteln haben wir uns damit beschäftigt, wie sich Geometrien verschieben, drehen und skalieren lassen. Verschiebung, Drehung und Skalierung werden als „Transformationen“ bezeichnet. Jede dieser Transformationen erforderte Änderungen am Shader und jede der drei Transformationen war reihenfolgeabhängig.

Hier ist beispielsweise eine Skalierung von 2, 1, eine Drehung von 30 % und eine Verschiebung von 100, 0 zu sehen.

Und hier ist eine Verschiebung von 100,0, eine Rotation von 30% und eine Skalierung von 2, 1:

Die Ergebnisse sind völlig unterschiedlich. Schlimmer noch: Wenn wir das zweite Beispiel benötigten, müssten wir einen anderen Shader schreiben, der die Translation, Rotation und Skalierung in der gewünschten Reihenfolge anwendet. Nun, einige Leute, die viel schlauer sind als ich, haben herausgefunden, dass man mit Matrizenrechnungen genau dieselben Dinge tun kann. Für 2D verwenden wir eine 3 × 3-Matrix. Eine 3 × 3-Matrix ist wie ein Raster mit 9 Feldern.

1.0	2.0	3
4.0	5	6.0
7.0	8.0	9.0

Für die Berechnung multiplizieren wir die Position in den Spalten der Matrix und addieren die Ergebnisse. Unsere Positionen haben nur zwei Werte, x und y. Für diese Berechnung benötigen wir jedoch drei Werte. Wir verwenden also „1“ als dritten Wert. In diesem Fall wäre unser Ergebnis

newX = x * 1.0 + y * 4.0 + 1 * 7.0

newY = x * 2.0 + y * 5.0 + 1 * 8.0

extra = x * 3.0 + y * 6.0 + 1 * 9.0

Sie denken jetzt wahrscheinlich: „WAS SOLL DAS?“ Angenommen, wir haben eine Übersetzung. Wir nennen den Betrag, den wir übersetzen möchten, tx und ty. Erstellen wir eine Matrix wie diese:

1.0	0,0	0,0
0,0	1	0,0
tx	ty	1.0

Und jetzt sehen wir uns

newX = x * 1.0 + y * 0.0 + 1 * tx

newY = x * 0.0 + y * 1.0 + 1 * ty

extra = x * 0.0 + y * 0.0 + 1 * 1

Wenn Sie sich an Ihre Algebra erinnern, können wir alle Stellen löschen, die mit Null multipliziert werden. Durch das Multiplizieren mit 1 passiert effektiv nichts. Sehen wir uns das Ganze vereinfacht an, um zu sehen, was passiert.

newX = x + tx;
newY = y + ty;

Und Extras, die uns nicht wirklich interessieren. Das sieht überraschenderweise dem Übersetzungscode aus unserem Übersetzungsbeispiel sehr ähnlich. Sehen wir uns nun die Drehung an. Wie bereits im Artikel zur Drehung erwähnt, benötigen wir nur den Sinus und den Kosinus des Winkels, um den wir drehen möchten.

s = Math.sin(angleToRotateInRadians);
c = Math.cos(angleToRotateInRadians);

Und wir erstellen eine Matrix wie diese:

c	-s	0,0
s	c	0,0
0,0	0,0	1.0

Wenn wir die Matrix anwenden, erhalten wir Folgendes:

newX = x * c + y * s + 1 * 0

newY = x * -s + y * c + 1 * 0

extra = x * 0.0 + y * 0.0 + 1 * 1

Wenn wir alle Nullen und Einsen ausradieren, erhalten wir

newX = x *  c + y * s;
newY = x * -s + y * c;

Genau das war in unserer Stichprobe der Fall. Und zuletzt: Maßstab. Wir nennen unsere beiden Skalierungsfaktoren sx und sy und erstellen eine Matrix wie diese:

sx	0,0	0,0
0,0	sy	0,0
0,0	0,0	1.0

Wenn wir die Matrix anwenden, erhalten wir Folgendes:

newX = x * sx + y * 0 + 1 * 0

newY = x * 0 + y * sy + 1 * 0

extra = x * 0.0 + y * 0.0 + 1 * 1

was wirklich

newX = x * sx;
newY = y * sy;

Das entspricht unserem Skalierungsbeispiel. Sie denken jetzt vielleicht: Was ist mein Vorteil? Was soll das? Das klingt nach viel Arbeit, nur um das Gleiche zu tun, was wir schon getan haben. Hier kommt die Magie ins Spiel. Es stellt sich heraus, dass wir Matrizen miteinander multiplizieren und alle Transformationen gleichzeitig anwenden können. Angenommen, wir haben die Funktion matrixMultiply, die zwei Matrizen nimmt, sie multipliziert und das Ergebnis zurückgibt. Um die Sache anschaulicher zu machen, erstellen wir Funktionen zum Erstellen von Matrizen für Verschiebung, Drehung und Skalierung.

function makeTranslation(tx, ty) {
  return [
    1, 0, 0,
    0, 1, 0,
    tx, ty, 1
  ];
}

function makeRotation(angleInRadians) {
  var c = Math.cos(angleInRadians);
  var s = Math.sin(angleInRadians);
  return [
    c,-s, 0,
    s, c, 0,
    0, 0, 1
  ];
}

function makeScale(sx, sy) {
  return [
    sx, 0, 0,
    0, sy, 0,
    0, 0, 1
  ];
}

Ändern wir jetzt den Shader. Der alte Shader sah so aus:

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;
uniform vec2 u_scale;

void main() {
  // Scale the positon
  vec2 scaledPosition = a_position * u_scale;

  // Rotate the position
  vec2 rotatedPosition = vec2(
     scaledPosition.x * u_rotation.y + scaledPosition.y * u_rotation.x,
     scaledPosition.y * u_rotation.y - scaledPosition.x * u_rotation.x);

  // Add in the translation.
  vec2 position = rotatedPosition + u_translation;
  ...

Unser neuer Shader wird viel einfacher sein.

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform mat3 u_matrix;

void main() {
  // Multiply the position by the matrix.
  vec2 position = (u_matrix * vec3(a_position, 1)).xy;
  ...

So verwenden wir sie

  // Draw the scene.
  function drawScene() {
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Compute the matrices
    var translationMatrix =
       makeTranslation(translation[0], translation[1]);
    var rotationMatrix = makeRotation(angleInRadians);
    var scaleMatrix = makeScale(scale[0], scale[1]);

    // Multiply the matrices.
    var matrix = matrixMultiply(scaleMatrix, rotationMatrix);
    matrix = matrixMultiply(matrix, translationMatrix);

    // Set the matrix.
    gl.uniformMatrix3fv(matrixLocation, false, matrix);

    // Draw the rectangle.
    gl.drawArrays(gl.TRIANGLES, 0, 18);
  }

Sie fragen sich vielleicht: Was soll das? Das scheint kein großer Vorteil zu sein . Wenn wir die Reihenfolge jedoch ändern möchten, müssen wir keinen neuen Shader schreiben. Wir können einfach die Mathematik ändern.

    ...
    // Multiply the matrices.
    var matrix = matrixMultiply(translationMatrix, rotationMatrix);
    matrix = matrixMultiply(matrix, scaleMatrix);
    ...

Die Möglichkeit, solche Matrizen anzuwenden, ist besonders wichtig für hierarchische Animationen wie Arme an einem Körper, Monde um einen Planeten oder Äste an einem Baum. Als einfaches Beispiel für eine hierarchische Animation zeichnen wir unser „F“ fünfmal, beginnen aber jedes Mal mit der Matrix des vorherigen „F“.

  // Draw the scene.
  function drawScene() {
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Compute the matrices
    var translationMatrix = makeTranslation(translation[0], translation[1]);
    var rotationMatrix = makeRotation(angleInRadians);
    var scaleMatrix = makeScale(scale[0], scale[1]);

    // Starting Matrix.
    var matrix = makeIdentity();

    for (var i = 0; i < 5; ++i) {
      // Multiply the matrices.
      matrix = matrixMultiply(matrix, scaleMatrix);
      matrix = matrixMultiply(matrix, rotationMatrix);
      matrix = matrixMultiply(matrix, translationMatrix);

      // Set the matrix.
      gl.uniformMatrix3fv(matrixLocation, false, matrix);

      // Draw the geometry.
      gl.drawArrays(gl.TRIANGLES, 0, 18);
    }
  }

Dazu haben wir die Funktion makeIdentity eingeführt, mit der eine Identitätsmatrix erstellt wird. Eine Identitätsmatrix ist eine Matrix, die effektiv 1.0 darstellt, sodass bei einer Multiplikation mit der Identität nichts passiert. Genau wie

X * 1 = X

matrixX * identity = matrixX

Hier ist der Code zum Erstellen einer Identitätsmatrix.

function makeIdentity() {
  return [
    1, 0, 0,
    0, 1, 0,
    0, 0, 1
  ];
}

Noch ein Beispiel: In allen bisherigen Beispielen dreht sich unser „F“ um seine linke obere Ecke. Das liegt daran, dass die verwendeten mathematischen Funktionen immer um den Ursprung rotieren und die linke obere Ecke von „F“ sich am Ursprung (0, 0) befindet. Da wir jetzt aber Matrizenmathematik anwenden und die Reihenfolge der angewendeten Transformationen auswählen können, können wir den Ursprung verschieben, bevor die restlichen Transformationen angewendet werden.

    // make a matrix that will move the origin of the 'F' to
    // its center.
    var moveOriginMatrix = makeTranslation(-50, -75);
    ...

    // Multiply the matrices.
    var matrix = matrixMultiply(moveOriginMatrix, scaleMatrix);
    matrix = matrixMultiply(matrix, rotationMatrix);
    matrix = matrixMultiply(matrix, translationMatrix);

So können Sie die Objekte von einem beliebigen Punkt aus drehen oder skalieren. Jetzt wissen Sie, wie Sie in Photoshop oder Flash den Drehpunkt verschieben. Aber es geht noch verrückter. Wenn Sie sich den ersten Artikel zu WebGL-Grundlagen noch einmal ansehen, erinnern Sie sich vielleicht, dass wir im Shader Code zur Umwandlung von Pixeln in Clipspace haben, der so aussieht:

  ...
  // convert the rectangle from pixels to 0.0 to 1.0
  vec2 zeroToOne = position / u_resolution;

  // convert from 0->1 to 0->2
  vec2 zeroToTwo = zeroToOne * 2.0;

  // convert from 0->2 to -1->+1 (clipspace)
  vec2 clipSpace = zeroToTwo - 1.0;

  gl_Position = vec4(clipSpace * vec2(1, -1), 0, 1);

Wenn Sie sich die einzelnen Schritte genauer ansehen, ist der erste Schritt, „von Pixeln in 0,0 bis 1,0 umwandeln“, in Wirklichkeit ein Skalierungsvorgang. Der zweite ist ebenfalls ein Skalierungsvorgang. Die nächste ist eine Verschiebung und die letzte skaliert Y um -1. Wir können das alles in der Matrix tun, die wir an den Shader übergeben. Wir könnten zwei Skalierungsmatrizen erstellen, eine zum Skalieren um 1,0/Auflösung, eine zum Skalieren um 2,0, eine dritte zum Verschieben um -1,0, -1,0 und eine vierte zum Skalieren von Y um -1 und sie dann alle miteinander multiplizieren. Da die Mathematik jedoch einfach ist, erstellen wir einfach eine Funktion, die direkt eine Projektionsmatrix für eine bestimmte Auflösung erstellt.

function make2DProjection(width, height) {
  // Note: This matrix flips the Y axis so that 0 is at the top.
  return [
    2 / width, 0, 0,
    0, -2 / height, 0,
    -1, 1, 1
  ];
}

Jetzt können wir den Shader noch weiter vereinfachen. Hier ist der vollständige neue Vertex-Shader.

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform mat3 u_matrix;

void main() {
  // Multiply the position by the matrix.
  gl_Position = vec4((u_matrix * vec3(a_position, 1)).xy, 0, 1);
}
</script>

Und in JavaScript müssen wir mit der Projektionsmatrix multiplizieren.

  // Draw the scene.
  function drawScene() {
    ...
    // Compute the matrices
    var projectionMatrix =
       make2DProjection(canvas.width, canvas.height);
    ...

    // Multiply the matrices.
    var matrix = matrixMultiply(scaleMatrix, rotationMatrix);
    matrix = matrixMultiply(matrix, translationMatrix);
    matrix = matrixMultiply(matrix, projectionMatrix);
    ...
  }

Außerdem haben wir den Code entfernt, mit dem die Auflösung festgelegt wurde. Mit diesem letzten Schritt sind wir von einem ziemlich komplizierten Shader mit 6 bis 7 Schritten zu einem sehr einfachen Shader mit nur einem Schritt übergegangen. Das ist alles der Magie der Matrizenmathematik zu verdanken.

Ich hoffe, dass dieser Artikel Ihnen dabei geholfen hat, die Matrixmathematik zu entmystifizieren. Als Nächstes geht es um 3D. In 3D-Matrizen gelten dieselben Prinzipien und Verwendungen. Ich habe mit 2D begonnen, um es möglichst einfach zu halten.