תרגום 2D ב-WebGL
לפני שנמשיך ל-3D, נישאר עוד קצת ב-2D. רק עוד רגע. יכול להיות שהמאמר הזה נראה לחלקכם מובן מאליו, אבל אגיע לעניין בהדרגה במספר מאמרים.
המאמר הזה הוא המשך של סדרה שמתחילה במאמר WebGL Fundamentals. אם לא קראת אותו, מומלץ לקרוא לפחות את הפרק הראשון ואז לחזור לכאן. 'תרגום' הוא שם מתחכם למדי של מושג מתמטיקה, שמשמעותו בעיקר 'העברה' של משהו. אני מניח שגם העברת משפט מאנגלית ליפנית מתאימה, אבל במקרה הזה אנחנו מדברים על העברת גיאומטריה. באמצעות הקוד לדוגמה שהגענו אליו בפוסט הראשון, אפשר לתרגם בקלות את המלבן שלנו רק על ידי שינוי הערכים המועברים ל-setRectangle, נכון? הנה דוגמה על סמך הדוגמה הקודמת.
// First lets make some variables
// to hold the translation of the rectangle
var translation = [0, 0];
// then let's make a function to
// re-draw everything. We can call this
// function after we update the translation.
// Draw the scene.
function drawScene() {
// Clear the canvas.
gl.clear(gl.COLOR_BUFFER_BIT);
// Setup a rectangle
setRectangle(gl, translation[0], translation[1], width, height);
// Draw the rectangle.
gl.drawArrays(gl.TRIANGLES, 0, 6);
}
עד עכשיו, הכול טוב ויפה. עכשיו נדמיין שרצינו לעשות את אותו הדבר עם צורה מורכבת יותר. נניח שרצינו לצייר אות F שמכילה 6 משולשים, כמו זה.

זה הקוד הנוכחי. נצטרך לשנות את setRectangle למשהו שדומה לזה.
// Fill the buffer with the values that define a letter 'F'.
function setGeometry(gl, x, y) {
var width = 100;
var height = 150;
var thickness = 30;
gl.bufferData(
gl.ARRAY_BUFFER,
new Float32Array([
// left column
x, y,
x + thickness, y,
x, y + height,
x, y + height,
x + thickness, y,
x + thickness, y + height,
// top rung
x + thickness, y,
x + width, y,
x + thickness, y + thickness,
x + thickness, y + thickness,
x + width, y,
x + width, y + thickness,
// middle rung
x + thickness, y + thickness * 2,
x + width * 2 / 3, y + thickness * 2,
x + thickness, y + thickness * 3,
x + thickness, y + thickness * 3,
x + width * 2 / 3, y + thickness * 2,
x + width * 2 / 3, y + thickness * 3]),
gl.STATIC_DRAW);
}
אני מקווה שברור לכם שזה לא יתאים להתאמה לעומס. אם רוצים לצייר גיאומטריה מורכבת מאוד עם מאות או אלפי שורות, צריך לכתוב קוד די מורכב. בנוסף, בכל פעם שאנחנו מציירים, JavaScript צריך לעדכן את כל הנקודות. יש דרך פשוטה יותר. פשוט מעלים את הגיאומטריה ומבצעים את התרגום בשדרן. הנה ה-shader החדש
<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;
uniform vec2 u_resolution;
uniform vec2 u_translation;
void main() {
// Add in the translation.
vec2 position = a_position + u_translation;
// convert the rectangle from pixels to 0.0 to 1.0
vec2 zeroToOne = position / u_resolution;
...
ונעצב מחדש את הקוד. ראשית, צריך להגדיר את הגיאומטריה רק פעם אחת.
// Fill the buffer with the values that define a letter 'F'.
function setGeometry(gl) {
gl.bufferData(
gl.ARRAY_BUFFER,
new Float32Array([
// left column
0, 0,
30, 0,
0, 150,
0, 150,
30, 0,
30, 150,
// top rung
30, 0,
100, 0,
30, 30,
30, 30,
100, 0,
100, 30,
// middle rung
30, 60,
67, 60,
30, 90,
30, 90,
67, 60,
67, 90]),
gl.STATIC_DRAW);
}
לאחר מכן, צריך רק לעדכן את u_translation לפני שאנחנו מציירים עם התרגום הרצוי.
...
var translationLocation = gl.getUniformLocation(
program, "u_translation");
...
// Set Geometry.
setGeometry(gl);
..
// Draw scene.
function drawScene() {
// Clear the canvas.
gl.clear(gl.COLOR_BUFFER_BIT);
// Set the translation.
gl.uniform2fv(translationLocation, translation);
// Draw the rectangle.
gl.drawArrays(gl.TRIANGLES, 0, 18);
}
שימו לב: הפונקציה setGeometry נקראת רק פעם אחת. הוא כבר לא נמצא בתוך drawScene.
עכשיו, כשאנחנו מציירים, WebGL עושה כמעט הכול. כל מה שאנחנו עושים הוא להגדיר תרגום ולבקש ממנו לצייר. גם אם לגיאומטריה שלנו היו עשרות אלפי נקודות, הקוד הראשי היה נשאר ללא שינוי.
סיבוב דו-ממדי ב-WebGL
אני רוצה להודות כבר מההתחלה שאין לי מושג אם ההסבר שלי יהיה הגיוני, אבל מה נורא, כדאי לנסות.
קודם כול, אני רוצה להציג לכם את מה שנקרא 'מעגל יחידה'. אם אתם זוכרים את המתמטיקה של חטיבת הביניים (אל תירדו לישון!) לעיגולים יש רדיוס. הרדיוס של מעגל הוא המרחק ממרכז המעגל לקצה שלו. מעגל יחידה הוא מעגל עם רדיוס של 1.0.
אם אתם זוכרים מתמטיקה בסיסית בכיתה ג', כשמעריכים מספר ב-1, הוא לא משתנה. לכן, 123 * 1 = 123. די בסיסי, נכון? עיגול יחידה, עיגול עם רדיוס של 1.0 הוא גם צורה של 1. זהו 1 מסתובב. כך אפשר להכפיל מספר מסוים ביחידה הזאת, ובאופן מסוים זה דומה להכפלה ב-1, חוץ מזה שמתרחש קסם והדברים מסתובבים. ניקח את ערכי X ו-Y מכל נקודה על מעגל היחידה, ונכפיל בהם את הגיאומטריה שלנו מהדוגמה הקודמת. אלה העדכונים לשימרים שלנו.
<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;
uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;
void main() {
// Rotate the position
vec2 rotatedPosition = vec2(
a_position.x * u_rotation.y + a_position.y * u_rotation.x,
a_position.y * u_rotation.y - a_position.x * u_rotation.x);
// Add in the translation.
vec2 position = rotatedPosition + u_translation;
אנחנו מעדכנים את ה-JavaScript כדי שנוכל להעביר את שני הערכים האלה.
...
var rotationLocation = gl.getUniformLocation(program, "u_rotation");
...
var rotation = [0, 1];
..
// Draw the scene.
function drawScene() {
// Clear the canvas.
gl.clear(gl.COLOR_BUFFER_BIT);
// Set the translation.
gl.uniform2fv(translationLocation, translation);
// Set the rotation.
gl.uniform2fv(rotationLocation, rotation);
// Draw the rectangle.
gl.drawArrays(gl.TRIANGLES, 0, 18);
}
למה זה עובד? חשבון פשוט.
rotatedX = a_position.x * u_rotation.y + a_position.y * u_rotation.x;
rotatedY = a_position.y * u_rotation.y - a_position.x * u_rotation.x;
נניח שיש לכם מלבן ואתם רוצים לסובב אותו. לפני שמתחילים לסובב אותו, הפינה השמאלית העליונה נמצאת ב-3.0, 9.0. נבחר נקודה במעגל היחידה ב-30 מעלות בכיוון השעון מ-12 בצהריים.
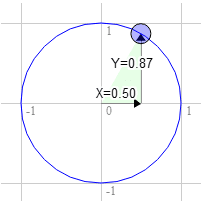
המיקום בתוך המעגל הוא 0.50 ו-0.87
3.0 * 0.87 + 9.0 * 0.50 = 7.1
9.0 * 0.87 - 3.0 * 0.50 = 6.3
זה בדיוק המיקום הרצוי

אותו הדבר עבור 60 מעלות בכיוון השעון
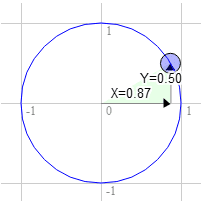
המיקום בתוך המעגל הוא 0.87 ו-0.50
3.0 * 0.50 + 9.0 * 0.87 = 9.3
9.0 * 0.50 - 3.0 * 0.87 = 1.9
אפשר לראות שככל שאנחנו מסובבים את הנקודה הזו בכיוון השעון ימינה, ערך X גדל וערך Y קטן. אם נמשיך מעבר ל-90 מעלות, הערך של X יתחיל לקטון שוב והערך של Y יתחיל לגדול. הדפוס הזה מאפשר לנו לבצע סיבוב. יש שם אחר לנקודות במעגל יחידה. הם נקראים סינוס וקוסינוס. כך, לכל זווית נתונה, אפשר פשוט לחפש את הסינוס והקוסינוס באופן הזה.
function printSineAndCosineForAnAngle(angleInDegrees) {
var angleInRadians = angleInDegrees * Math.PI / 180;
var s = Math.sin(angleInRadians);
var c = Math.cos(angleInRadians);
console.log("s = " + s + " c = " + c);
}
אם מעתיקים את הקוד ומדביקים אותו במסוף JavaScript ומקלידים printSineAndCosignForAngle(30), יופיע הערך s = 0.49 c= 0.87 (הערה: עיגול המספרים).
אם משלבים את כל הרכיבים האלה, אפשר לסובב את הגיאומטריה לכל זווית שרוצים. פשוט מגדירים את הסיבוב לפי הסינוס והקוסינוס של הזווית שאליה רוצים לסובב.
...
var angleInRadians = angleInDegrees * Math.PI / 180;
rotation[0] = Math.sin(angleInRadians);
rotation[1] = Math.cos(angleInRadians);
אני מקווה שהסברתי את זה בצורה ברורה. עכשיו נסביר על דרך פשוטה יותר. קנה מידה.
מהם רדיאנים?
רדיאן היא יחידת מידה שמשמשת במעגלים, בתנועה סיבובית ובזוויות. בדיוק כמו שאפשר למדוד מרחק בסנטימטרים, ביארד, במטרים וכו', אפשר למדוד זוויות במעלות או ברדיאנים.
סביר להניח שאתם יודעים שקל יותר לבצע פעולות מתמטיות עם מדידות מטריות מאשר עם מדידות בריטים. כדי לעבור מאינטש לרגלים, מחלקים ב-12. כדי לעבור מאינץ' ליארדים, מחלקים ב-36. לא יודע מה איתך, אבל אני לא מצליח לחלק ב-36 בראש. עם מדד, זה הרבה יותר קל. כדי לעבור ממילימטרים לסנטימטרים, מחלקים ב-10. כדי לעבור ממילימטרים למטרים, צריך לחלק ב-1,000. אני יכול לחלוק ב-1,000 בראש.
רדיאנים לעומת מעלות הם דומים. החשבון מסתבך כשמשתמשים בתחומים. בעזרת רדיאנים, החשבון קל. יש 360 מעלות במעגל, אבל יש רק 2π רדיאנים. לכן, סיבוב מלא הוא 2π רדיאנים. חצי סיבוב הוא π רדיאנים. סיבוב של 1/4, כלומר 90 מעלות, הוא π/2 רדיאן. לכן, אם רוצים לסובב משהו ב-90 מעלות, פשוט משתמשים ב-Math.PI * 0.5. אם רוצים לסובב אותו ב-45 מעלות, משתמשים ב-Math.PI * 0.25 וכו'.
כמעט כל החישובים המתמטיים שכוללים זוויות, עיגולים או סיבוב פועלים בצורה פשוטה מאוד אם מתחילים לחשוב ברדיאנים. כדאי לנסות. יש להשתמש ברדיאנים ולא במעלות, מלבד בתצוגות של ממשק המשתמש.
קנה מידה 2D ב-WebGL
התאמה לעומס מתבצעת בקלות רבה, בדיוק כמו התרגום.
אנחנו מכפילים את המיקום בסולם הרצוי. אלה השינויים מהדוגמה הקודמת שלנו.
<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;
uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;
uniform vec2 u_scale;
void main() {
// Scale the positon
vec2 scaledPosition = a_position * u_scale;
// Rotate the position
vec2 rotatedPosition = vec2(
scaledPosition.x * u_rotation.y +
scaledPosition.y * u_rotation.x,
scaledPosition.y * u_rotation.y -
scaledPosition.x * u_rotation.x);
// Add in the translation.
vec2 position = rotatedPosition + u_translation;
מוסיפים את ה-JavaScript הנדרש להגדרת קנה המידה בזמן הציור.
...
var scaleLocation = gl.getUniformLocation(program, "u_scale");
...
var scale = [1, 1];
...
// Draw the scene.
function drawScene() {
// Clear the canvas.
gl.clear(gl.COLOR_BUFFER_BIT);
// Set the translation.
gl.uniform2fv(translationLocation, translation);
// Set the rotation.
gl.uniform2fv(rotationLocation, rotation);
// Set the scale.
gl.uniform2fv(scaleLocation, scale);
// Draw the rectangle.
gl.drawArrays(gl.TRIANGLES, 0, 18);
}
חשוב לשים לב שכאשר משנים את הגודל לפי ערך שלילי, הגיאומטריה שלנו מתהפכת. אני מקווה ש-3 הפרקים האחרונים עזרו לך להבין את התרגום, הסיבוב והשינוי של קנה המידה. בשלב הבא נדבר על המטריצות הקסומות שמשלבות את כל 3 הרכיבים האלה בצורה פשוטה בהרבה, ולרוב גם שימושית יותר.
למה 'F'?
הפעם הראשונה שראיתי מישהו משתמש באות F הייתה בטקסטורה. האות F עצמה לא חשובה. חשוב שתוכלו לזהות את הכיוון שלו מכל כיוון. לדוגמה, אם היינו משתמשים בלב ♥ או במשולש △, לא היינו יכולים לדעת אם הוא הופך אופקית. מעגל ○ יהיה אפילו גרוע יותר. אפשר להשתמש גם בריבוע צבעוני עם צבעים שונים בכל פינה, אבל אז תצטרכו לזכור איזה פינה היא איזו. כיוון האות F מיד מזוהה.

כל צורה שאפשר לזהות את הכיוון שלה תעבוד. אני משתמש ב-'F' מאז 'F'ירסט שמעתי על הרעיון.
מטריצות 2D ב-WebGL
ב-3 הפרקים האחרונים הוסבר איך לבצע תרגום של גיאומטריה, סיבוב של גיאומטריה ושינוי קנה המידה של גיאומטריה. תרגום, סיבוב וגודל נחשבים כל אחד לסוג של 'טרנספורמציה'. כל אחד מהטרנספורמציות האלה נדרש שינויים בשיידר, וכל אחת מ-3 הטרנספורמציות הייתה תלויה בסדר.
לדוגמה, הנה שינוי קנה מידה של 2, 1, סיבוב של 30% ותרגום של 100, 0.

וזו תזוזה של 100,0, סיבוב של 30% ושינוי קנה מידה של 2, 1

התוצאות הן שונות לחלוטין. גרוע מכך, אם היינו צריכים את הדוגמה השנייה, היינו צריכים לכתוב שדר אחר שיחיל את התרגום, הסיבוב וההתאמה בסדר החדש הרצוי. אנשים חכמים בהרבה ממני הבינו שאפשר לעשות את כל אותם דברים באמצעות מתמטיקה של מטריצות. ב-2D אנחנו משתמשים במטריצה 3x3. מטריצה בגודל 3x3 היא כמו רשת עם 9 תיבות.
| 1.0 | 2.0 | 3.0 |
| 4.0 | 5.0 | 6.0 |
| 7.0 | 8.0 | 9.0 |
כדי לבצע את החישוב, מכפילים את המיקום בעמודות של המטריצה ומסכמים את התוצאות. למיקומים שלנו יש רק 2 ערכים, x ו-y, אבל כדי לבצע את החישוב הזה נדרשים 3 ערכים, לכן נשתמש ב-1 כערך השלישי. במקרה הזה התוצאה תהיה
newX = x * 1.0 + y * 4.0 + 1 * 7.0
newY = x * 2.0 + y * 5.0 + 1 * 8.0
extra = x * 3.0 + y * 6.0 + 1 * 9.0
כנראה שאתם קוראים את זה וחושבים "מה העניין?". נניח שיש לנו תרגום. נקרא לסכום שרוצים לתרגם tx ו-ty. נוצרת מטריצת משנה כזו
| 1.0 | 0.0 | 0.0 |
| 0.0 | 1.0 | 0.0 |
| tx | ty | 1.0 |
עכשיו אפשר לבדוק
newX = x * 1.0 + y * 0.0 + 1 * tx
newY = x * 0.0 + y * 1.0 + 1 * ty
extra = x * 0.0 + y * 0.0 + 1 * 1
אם אתם זוכרים את האלגברה, אפשר למחוק כל מקום שבו מתבצעת כפל באפס. כפל ב-1 לא עושה כלום, אז ננסה לפשט כדי לראות מה קורה
newX = x + tx;
newY = y + ty;
ועוד דברים שלא ממש מעניינים אותנו. הקוד הזה נראה דומה להפתיע לקוד התרגום מדוגמת התרגום שלנו. באופן דומה, נבצע סיבוב. כפי שציינו בפוסט על רוטציה, אנחנו צריכים רק את הסינוס והקוסינוס של הזווית שבה אנחנו רוצים לבצע את הסיבוב.
s = Math.sin(angleToRotateInRadians);
c = Math.cos(angleToRotateInRadians);
ובונים מטריצה כזו
| c | -s | 0.0 |
| s | c | 0.0 |
| 0.0 | 0.0 | 1.0 |
החלת המטריצה מובילה לביטוי הבא
newX = x * c + y * s + 1 * 0
newY = x * -s + y * c + 1 * 0
extra = x * 0.0 + y * 0.0 + 1 * 1
אם נסמן בקו שחור את כל המכפילים של 0 ו-1, נקבל
newX = x * c + y * s;
newY = x * -s + y * c;
זה בדיוק מה שהיה לנו בדגימת הרוטינת. ולבסוף, התאמה לעומס. נקרא לשני גורמי ההתאמה sx ו-sy ונבנה מטריקס כזה
| sx | 0.0 | 0.0 |
| 0.0 | sy | 0.0 |
| 0.0 | 0.0 | 1.0 |
החלת המטריצה מובילה לביטוי הבא
newX = x * sx + y * 0 + 1 * 0
newY = x * 0 + y * sy + 1 * 0
extra = x * 0.0 + y * 0.0 + 1 * 1
שזה ממש
newX = x * sx;
newY = y * sy;
זהו אותו ערך כמו בדוגמה שלנו להתאמה לעומס.
אני מניח שעדיין יש לך שאלות. אז מה? מה הטעם. נראה שזו עבודה רבה רק כדי לעשות את אותו הדבר שכבר עשינו?
כאן מתחיל הקסם. מסתבר שאפשר להכפיל מטריצות זו בזו ולהחיל את כל הטרנספורמציות בבת אחת. נניח שיש לנו פונקציה, matrixMultiply, שמקבלת שתי מטריצות, מכפילה אותן ומחזירה את התוצאה.
כדי להבהיר את הנושא, נגדיר פונקציות ליצירת מטריצות עבור תרגום, סיבוב וגודל.
function makeTranslation(tx, ty) {
return [
1, 0, 0,
0, 1, 0,
tx, ty, 1
];
}
function makeRotation(angleInRadians) {
var c = Math.cos(angleInRadians);
var s = Math.sin(angleInRadians);
return [
c,-s, 0,
s, c, 0,
0, 0, 1
];
}
function makeScale(sx, sy) {
return [
sx, 0, 0,
0, sy, 0,
0, 0, 1
];
}
עכשיו נשנה את ה-shader. ה-shader הישן נראה כך
<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;
uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;
uniform vec2 u_scale;
void main() {
// Scale the positon
vec2 scaledPosition = a_position * u_scale;
// Rotate the position
vec2 rotatedPosition = vec2(
scaledPosition.x * u_rotation.y + scaledPosition.y * u_rotation.x,
scaledPosition.y * u_rotation.y - scaledPosition.x * u_rotation.x);
// Add in the translation.
vec2 position = rotatedPosition + u_translation;
...
ה-shader החדש שלנו יהיה פשוט הרבה יותר.
<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;
uniform vec2 u_resolution;
uniform mat3 u_matrix;
void main() {
// Multiply the position by the matrix.
vec2 position = (u_matrix * vec3(a_position, 1)).xy;
...
וזה האופן שבו אנחנו משתמשים בה
// Draw the scene.
function drawScene() {
// Clear the canvas.
gl.clear(gl.COLOR_BUFFER_BIT);
// Compute the matrices
var translationMatrix =
makeTranslation(translation[0], translation[1]);
var rotationMatrix = makeRotation(angleInRadians);
var scaleMatrix = makeScale(scale[0], scale[1]);
// Multiply the matrices.
var matrix = matrixMultiply(scaleMatrix, rotationMatrix);
matrix = matrixMultiply(matrix, translationMatrix);
// Set the matrix.
gl.uniformMatrix3fv(matrixLocation, false, matrix);
// Draw the rectangle.
gl.drawArrays(gl.TRIANGLES, 0, 18);
}
אבל אולי אתם שואלים, אז מה? נראה שזה לא ממש יתרון . אבל עכשיו, אם אנחנו רוצים לשנות את הסדר, אנחנו לא צריכים לכתוב שדר חדש. אנחנו יכולים פשוט לשנות את החישוב.
...
// Multiply the matrices.
var matrix = matrixMultiply(translationMatrix, rotationMatrix);
matrix = matrixMultiply(matrix, scaleMatrix);
...
היכולת להחיל מטריצות כאלה חשובה במיוחד לאנימציה היררכית, כמו זרועות בגוף, ירחים בכוכב סביב השמש או ענפים בעץ. לדוגמה פשוטה של אנימציה היררכית, נצייר את 'F' שלנו 5 פעמים, אבל בכל פעם נתחיל מהמטריצה של 'F' הקודם.
// Draw the scene.
function drawScene() {
// Clear the canvas.
gl.clear(gl.COLOR_BUFFER_BIT);
// Compute the matrices
var translationMatrix = makeTranslation(translation[0], translation[1]);
var rotationMatrix = makeRotation(angleInRadians);
var scaleMatrix = makeScale(scale[0], scale[1]);
// Starting Matrix.
var matrix = makeIdentity();
for (var i = 0; i < 5; ++i) {
// Multiply the matrices.
matrix = matrixMultiply(matrix, scaleMatrix);
matrix = matrixMultiply(matrix, rotationMatrix);
matrix = matrixMultiply(matrix, translationMatrix);
// Set the matrix.
gl.uniformMatrix3fv(matrixLocation, false, matrix);
// Draw the geometry.
gl.drawArrays(gl.TRIANGLES, 0, 18);
}
}
כדי לעשות זאת, הכנסנו את הפונקציה makeIdentity, שיוצרת מטריצת זהות. מטריצה זהות היא מטריצה שמייצגת למעשה את הערך 1.0, כך שאם מכפילים במטריצה הזהות, לא קורה כלום. בדיוק כמו
X * 1 = X
כך גם
matrixX * identity = matrixX
זהו הקוד ליצירת מטריצת זהות.
function makeIdentity() {
return [
1, 0, 0,
0, 1, 0,
0, 0, 1
];
}
דוגמה נוספת: בכל דגימה עד כה, האות 'F' מסתובבת סביב הפינה הימנית העליונה שלה. הסיבה לכך היא שהמתמטיקה שבה אנחנו משתמשים תמיד מסתובבת סביב המקור, והפינה הימנית העליונה של 'F' נמצאת במקור, (0, 0) אבל עכשיו, מכיוון שאנחנו יכולים לבצע מתמטיקה של מטריצות ולבחור את הסדר שבו ההמרות חלות, אנחנו יכולים להזיז את המקור לפני שכל שאר ההמרות חלות.
// make a matrix that will move the origin of the 'F' to
// its center.
var moveOriginMatrix = makeTranslation(-50, -75);
...
// Multiply the matrices.
var matrix = matrixMultiply(moveOriginMatrix, scaleMatrix);
matrix = matrixMultiply(matrix, rotationMatrix);
matrix = matrixMultiply(matrix, translationMatrix);
בעזרת השיטה הזו אפשר לסובב או לשנות את קנה המידה מכל נקודה. עכשיו אתם יודעים איך אפשר להזיז את נקודת הסיבוב ב-Photoshop או ב-Flash. נמשיך להתפרע. אם חוזרים למאמר הראשון בנושא יסודות WebGL, אולי תזכרו שיש לנו קוד בשיידר להמרה מפיקסלים למרחב חיתוך שנראה כך.
...
// convert the rectangle from pixels to 0.0 to 1.0
vec2 zeroToOne = position / u_resolution;
// convert from 0->1 to 0->2
vec2 zeroToTwo = zeroToOne * 2.0;
// convert from 0->2 to -1->+1 (clipspace)
vec2 clipSpace = zeroToTwo - 1.0;
gl_Position = vec4(clipSpace * vec2(1, -1), 0, 1);
אם נבחן כל אחד מהשלבים האלה בתורו, השלב הראשון, 'המרה מפיקסלים ל-0.0 עד 1.0', הוא למעשה פעולת שינוי קנה מידה. השנייה היא גם פעולת שינוי קנה מידה. הפונקציה הבאה היא תרגום, והפונקציה האחרונה מגדילה את Y ב-1. אפשר לעשות את כל זה במטריצה שאנחנו מעבירים לשיח. אפשר ליצור 2 מטריצות שינוי-מידה, אחת להגדלת המידה ב-1.0/רזולוציה, אחת להגדלת המידה ב-2.0, שלישית להזזה ב-1.0,-1.0 ורביעית להגדלת המידה של Y ב-1, ואז להכפיל את כולן יחד. אבל במקום זאת, מכיוון שהמתמטיקה פשוטה, פשוט ניצור פונקציה שיוצרת מטריצה של 'השלכה' לרזולוציה נתונה ישירות.
function make2DProjection(width, height) {
// Note: This matrix flips the Y axis so that 0 is at the top.
return [
2 / width, 0, 0,
0, -2 / height, 0,
-1, 1, 1
];
}
עכשיו אפשר לפשט את ה-shader עוד יותר. זהו ה-vertex shader החדש המלא.
<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;
uniform mat3 u_matrix;
void main() {
// Multiply the position by the matrix.
gl_Position = vec4((u_matrix * vec3(a_position, 1)).xy, 0, 1);
}
</script>
וב-JavaScript צריך להכפיל במטריצת ההקרנה
// Draw the scene.
function drawScene() {
...
// Compute the matrices
var projectionMatrix =
make2DProjection(canvas.width, canvas.height);
...
// Multiply the matrices.
var matrix = matrixMultiply(scaleMatrix, rotationMatrix);
matrix = matrixMultiply(matrix, translationMatrix);
matrix = matrixMultiply(matrix, projectionMatrix);
...
}
הסרנו גם את הקוד שמגדיר את הרזולוציה. בעזרת השלב האחרון הזה, עברנו משיח מורכב למדי עם 6-7 שלבים לשיח פשוט מאוד עם שלב אחד בלבד, והכל בזכות הקסם של מתמטיקה של מטריצות.
אני מקווה שהמאמר הזה עזר לכם להבין את המתמטיקה של מטריצות. עכשיו אעבור ל-3D. בחשבון של מטריצות תלת-ממדיות, העקרונות והשימוש זהים. התחלתי עם 2D כדי שיהיה קל להבין.

