Se usó la API de Cloud Translation para traducir esta página.

Transformaciones de WebGL

Gregg Tavares

Traducción 2D de WebGL

Antes de pasar al 3D, continuemos con el 2D un poco más. Espera un momento, por favor. Este artículo puede parecer demasiado obvio para algunos, pero llegaré a un punto en algunos artículos.

Este artículo es una continuación de una serie que comienza con Conceptos básicos de WebGL. Si no lo hiciste, te sugiero que leas al menos el primer capítulo y, luego, vuelvas a esta conversación. La traducción es un nombre matemático elegante que básicamente significa “mover” algo. Supongo que mover una oración del inglés al japonés también es adecuado, pero en este caso estamos hablando de mover la geometría. Con el código de muestra que obtuvimos en la primera publicación, podrías traducir fácilmente nuestro rectángulo con solo cambiar los valores que se pasan a setRectangle, ¿no? Este es un ejemplo basado en nuestro ejemplo anterior.

  // First lets make some variables 
  // to hold the translation of the rectangle
  var translation = [0, 0];
  // then let's make a function to
  // re-draw everything. We can call this
  // function after we update the translation.
  // Draw the scene.
  function drawScene() {
     // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);
    // Setup a rectangle
    setRectangle(gl, translation[0], translation[1], width, height);

    // Draw the rectangle.
    gl.drawArrays(gl.TRIANGLES, 0, 6);
  }

Hasta ahora, todo bien. Pero ahora imagina que queremos hacer lo mismo con una forma más complicada. Supongamos que queremos dibujar una "F" que consta de 6 triángulos como este.

Bueno, a continuación, se muestra el código actual que tendríamos que cambiar de setRectangle a algo más parecido a esto.

// Fill the buffer with the values that define a letter 'F'.
function setGeometry(gl, x, y) {
  var width = 100;
  var height = 150;
  var thickness = 30;
  gl.bufferData(
      gl.ARRAY_BUFFER,
      new Float32Array([
          // left column
          x, y,
          x + thickness, y,
          x, y + height,
          x, y + height,
          x + thickness, y,
          x + thickness, y + height,

          // top rung
          x + thickness, y,
          x + width, y,
          x + thickness, y + thickness,
          x + thickness, y + thickness,
          x + width, y,
          x + width, y + thickness,

          // middle rung
          x + thickness, y + thickness * 2,
          x + width * 2 / 3, y + thickness * 2,
          x + thickness, y + thickness * 3,
          x + thickness, y + thickness * 3,
          x + width * 2 / 3, y + thickness * 2,
          x + width * 2 / 3, y + thickness * 3]),
      gl.STATIC_DRAW);
}

Espero que puedas ver que no se escalará bien. Si queremos dibujar una geometría muy compleja con cientos o miles de líneas, tendríamos que escribir un código bastante complejo. Además, cada vez que dibujamos, JavaScript debe actualizar todos los puntos. Hay una forma más sencilla. Solo sube la geometría y realiza la traducción en el sombreador. Este es el nuevo sombreador

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform vec2 u_translation;

void main() {
   // Add in the translation.
   vec2 position = a_position + u_translation;

   // convert the rectangle from pixels to 0.0 to 1.0
   vec2 zeroToOne = position / u_resolution;
   ...

y reestructuraremos un poco el código. Por un lado, solo necesitamos configurar la geometría una vez.

// Fill the buffer with the values that define a letter 'F'.
function setGeometry(gl) {
  gl.bufferData(
      gl.ARRAY_BUFFER,
      new Float32Array([
          // left column
          0, 0,
          30, 0,
          0, 150,
          0, 150,
          30, 0,
          30, 150,

          // top rung
          30, 0,
          100, 0,
          30, 30,
          30, 30,
          100, 0,
          100, 30,

          // middle rung
          30, 60,
          67, 60,
          30, 90,
          30, 90,
          67, 60,
          67, 90]),
      gl.STATIC_DRAW);
}

Luego, solo debemos actualizar u_translation antes de dibujar con la traducción que deseamos.

  ...
  var translationLocation = gl.getUniformLocation(
             program, "u_translation");
  ...
  // Set Geometry.
  setGeometry(gl);
  ..
  // Draw scene.
  function drawScene() {
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Set the translation.
    gl.uniform2fv(translationLocation, translation);

    // Draw the rectangle.
    gl.drawArrays(gl.TRIANGLES, 0, 18);
  }

Observa que solo se llama a setGeometry una vez. Ya no está dentro de drawScene.

Ahora, cuando dibujamos, WebGL hace prácticamente todo. Todo lo que hacemos es establecer una traducción y pedirle que dibuje. Incluso si nuestra geometría tuviera decenas de miles de puntos, el código principal seguiría siendo el mismo.

Rotación 2D de WebGL

Voy a admitir de inmediato que no tengo idea de si la forma en que lo explicaré tendrá sentido, pero, ¿qué más da?, igual vale la pena intentarlo.

Primero, quiero presentarte lo que se llama un “círculo unitario”. Si recuerdas las matemáticas de la secundaria (¡no te duermas!), un círculo tiene un radio. El radio de un círculo es la distancia desde el centro del círculo hasta el borde. Un círculo unitario es un círculo con un radio de 1.0.

Si recuerdas las matemáticas básicas del tercer grado, si multiplicas algo por 1, el resultado sigue siendo el mismo. Por lo tanto, 123 × 1 = 123. Es bastante básico, ¿no? Bueno, un círculo unitario, un círculo con un radio de 1.0, también es una forma de 1. Es un 1 rotativo. Por lo tanto, puedes multiplicar algo por este círculo unitario y, de alguna manera, es como multiplicar por 1, excepto que sucede la magia y las cosas rotan. Tomaremos ese valor de X e Y de cualquier punto del círculo unitario y multiplicaremos nuestra geometría por ellos desde nuestro ejemplo anterior. Estas son las actualizaciones de nuestro sombreador.

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;

void main() {
  // Rotate the position
  vec2 rotatedPosition = vec2(
     a_position.x * u_rotation.y + a_position.y * u_rotation.x,
     a_position.y * u_rotation.y - a_position.x * u_rotation.x);

  // Add in the translation.
  vec2 position = rotatedPosition + u_translation;

Y actualizamos el código JavaScript para que podamos pasar esos 2 valores.

  ...
  var rotationLocation = gl.getUniformLocation(program, "u_rotation");
  ...
  var rotation = [0, 1];
  ..
  // Draw the scene.
  function drawScene() {
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Set the translation.
    gl.uniform2fv(translationLocation, translation);

    // Set the rotation.
    gl.uniform2fv(rotationLocation, rotation);

    // Draw the rectangle.
    gl.drawArrays(gl.TRIANGLES, 0, 18);
  }

¿Por qué funciona? Bueno, observa los cálculos.

rotatedX = a_position.x * u_rotation.y + a_position.y * u_rotation.x;
rotatedY = a_position.y * u_rotation.y - a_position.x * u_rotation.x;

Supongamos que tienes un rectángulo y quieres rotarlo. Antes de comenzar a rotarla, la esquina superior derecha está en 3.0, 9.0. Elige un punto en el círculo unitario a 30 grados en el sentido de las manecillas del reloj desde las 12 en punto.

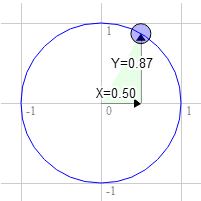
La posición en el círculo es 0.50 y 0.87.

3.0 * 0.87 + 9.0 * 0.50 = 7.1
9.0 * 0.87 - 3.0 * 0.50 = 6.3

Esa es exactamente la ubicación que necesitamos

Lo mismo sucede con 60 grados en el sentido de las manecillas del reloj.

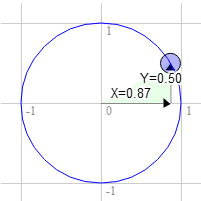
La posición en el círculo es 0.87 y 0.50.

3.0 * 0.50 + 9.0 * 0.87 = 9.3
9.0 * 0.50 - 3.0 * 0.87 = 1.9

Puedes ver que, a medida que rotamos ese punto en el sentido de las manecillas del reloj hacia la derecha, el valor de X aumenta y el de Y disminuye. Si se sigue pasando de 90 grados, X comenzaría a disminuir nuevamente y Y comenzaría a aumentar. Ese patrón nos da la rotación. Hay otro nombre para los puntos de un círculo unitario. Se llaman seno y coseno. Por lo tanto, para cualquier ángulo determinado, podemos buscar el seno y el coseno de esta manera.

function printSineAndCosineForAnAngle(angleInDegrees) {
  var angleInRadians = angleInDegrees * Math.PI / 180;
  var s = Math.sin(angleInRadians);
  var c = Math.cos(angleInRadians);
  console.log("s = " + s + " c = " + c);
}

Si copias y pegas el código en la consola de JavaScript y escribes printSineAndCosignForAngle(30), verás que imprime s = 0.49 c= 0.87 (nota: redondeé los números). Si lo unes todo, puedes rotar la geometría a cualquier ángulo que desees. Solo debes establecer la rotación en el seno y el coseno del ángulo al que deseas rotar.

  ...
  var angleInRadians = angleInDegrees * Math.PI / 180;
  rotation[0] = Math.sin(angleInRadians);
  rotation[1] = Math.cos(angleInRadians);

Espero que esto te haya resultado útil. A continuación, una más sencilla. Escala.

¿Qué son los radianes?

Los radianes son una unidad de medida que se usa con círculos, rotación y ángulos. Así como podemos medir la distancia en pulgadas, yardas, metros, etc., podemos medir los ángulos en grados o radianes.

Es probable que sepas que las matemáticas con mediciones métricas son más fáciles que las matemáticas con mediciones imperiales. Para pasar de pulgadas a pies, dividimos por 12. Para pasar de pulgadas a yardas, dividimos por 36. No sé tú, pero no puedo dividir por 36 mentalmente. Con la métrica, es mucho más fácil. Para pasar de milímetros a centímetros, dividimos por 10. Para pasar de milímetros a metros, dividimos por 1,000. Puedo dividir por 1,000 mentalmente.

Los radianes y los grados son similares. Los grados dificultan los cálculos. Los radianes facilitan los cálculos. Hay 360 grados en un círculo, pero solo hay 2π radianes. Por lo tanto, un giro completo es de 2π radianes. Un medio giro es π radianes. Un cuarto de vuelta, es decir, 90 grados, es π/2 radianes. Por lo tanto, si quieres rotar algo 90 grados, solo usa Math.PI * 0.5. Si quieres rotarlo 45 grados, usa Math.PI * 0.25, etcétera.

Casi todas las matemáticas que involucran ángulos, círculos o rotación funcionan de forma muy sencilla si empiezas a pensar en radianes. Pruébalo. Usa radianes, no grados, excepto en las pantallas de la IU.

Escala 2D de WebGL

El escalamiento es tan fácil como la traducción.

Multiplicamos la posición por la escala deseada. Estos son los cambios de nuestro ejemplo anterior.

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;
uniform vec2 u_scale;

void main() {
  // Scale the positon
  vec2 scaledPosition = a_position * u_scale;

  // Rotate the position
  vec2 rotatedPosition = vec2(
     scaledPosition.x * u_rotation.y +
        scaledPosition.y * u_rotation.x,
     scaledPosition.y * u_rotation.y -
        scaledPosition.x * u_rotation.x);

  // Add in the translation.
  vec2 position = rotatedPosition + u_translation;

y agregamos el código JavaScript necesario para establecer la escala cuando dibujamos.

  ...
  var scaleLocation = gl.getUniformLocation(program, "u_scale");
  ...
  var scale = [1, 1];
  ...
  // Draw the scene.
  function drawScene() {
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Set the translation.
    gl.uniform2fv(translationLocation, translation);

    // Set the rotation.
    gl.uniform2fv(rotationLocation, rotation);

    // Set the scale.
    gl.uniform2fv(scaleLocation, scale);

    // Draw the rectangle.
    gl.drawArrays(gl.TRIANGLES, 0, 18);
  }

Una cosa que debes tener en cuenta es que escalar por un valor negativo invierte nuestra geometría. Espero que estos últimos 3 capítulos te hayan resultado útiles para comprender la traslación, la rotación y la escala. A continuación, analizaremos la magia de las matrices que combinan los 3 en una forma mucho más simple y, a menudo, más útil.

¿Por qué una "F"?

La primera vez que vi a alguien usar una "F" fue en una textura. La "F" en sí no es importante. Lo importante es que puedas determinar su orientación desde cualquier dirección. Si usáramos un corazón ♥ o un triángulo △, por ejemplo, no podríamos saber si se invirtió horizontalmente. Un círculo ○ sería aún peor. Se podría argumentar que un rectángulo de color funcionaría con diferentes colores en cada esquina, pero luego tendrías que recordar cuál es cada esquina. La orientación de una F se reconoce de inmediato.

Cualquier forma de la que puedas indicar la orientación funcionaría. Solo he usado la "F" desde que me presentaron la idea.

Matrices 2D de WebGL

En los últimos 3 capítulos, revisamos cómo traducir, rotar y escalar la geometría. La traslación, la rotación y la escala se consideran un tipo de "transformación". Cada una de estas transformaciones requirió cambios en el sombreador, y cada una de las 3 transformaciones dependía del orden.

Por ejemplo, aquí hay una escala de 2, 1, una rotación del 30% y una traducción de 100, 0.

Y esta es una traducción de 100,0, una rotación del 30% y una escala de 2, 1.

Los resultados son completamente diferentes. Peor aún, si necesitáramos el segundo ejemplo, tendríamos que escribir un sombreador diferente que aplicara la traducción, la rotación y la escala en el nuevo orden deseado. Bueno, algunas personas mucho más inteligentes que yo descubrieron que puedes hacer lo mismo con las matemáticas matriciales. Para 2D, usamos una matriz de 3 × 3. Una matriz de 3 × 3 es como una cuadrícula con 9 cuadros.

1.0	2.0	3.0
4.0	5.0	6.0
7.0	8.0	9.0

Para hacer los cálculos, multiplicamos la posición por las columnas de la matriz y sumamos los resultados. Nuestras posiciones solo tienen 2 valores, x e y, pero para hacer esta operación matemática necesitamos 3 valores, por lo que usaremos 1 para el tercer valor. En este caso, nuestro resultado sería

newX = x * 1.0 + y * 4.0 + 1 * 7.0

newY = x * 2.0 + y * 5.0 + 1 * 8.0

extra = x * 3.0 + y * 6.0 + 1 * 9.0

Es probable que lo mires y pienses "¿PARA QUÉ SIRVE?". Bueno, supongamos que tenemos una traducción. Llamaremos tx y ty al importe que queremos traducir. Construyamos una matriz como esta

1.0	0.0	0.0
0.0	1.0	0.0
tx	ty	1.0

Y ahora, compruébalo

newX = x * 1.0 + y * 0.0 + 1 * tx

newY = x * 0.0 + y * 1.0 + 1 * ty

extra = x * 0.0 + y * 0.0 + 1 * 1

Si recuerdas el álgebra, podemos borrar cualquier lugar que se multiplique por cero. Multiplicar por 1 no hace nada, así que simplifiquemos para ver qué sucede.

newX = x + tx;
newY = y + ty;

Y no nos importa demasiado lo que sea adicional. Se parece sorprendentemente al código de traducción de nuestro ejemplo de traducción. Del mismo modo, hagamos la rotación. Como señalamos en la publicación sobre la rotación, solo necesitamos el seno y el coseno del ángulo en el que queremos rotar.

s = Math.sin(angleToRotateInRadians);
c = Math.cos(angleToRotateInRadians);

Y creamos una matriz como esta

c	-s	0.0
s	c	0.0
0.0	0.0	1.0

Si aplicamos la matriz, obtenemos lo siguiente:

newX = x * c + y * s + 1 * 0

newY = x * -s + y * c + 1 * 0

extra = x * 0.0 + y * 0.0 + 1 * 1

Si ocultamos todas las multiplicaciones por 0 y 1, obtenemos

newX = x *  c + y * s;
newY = x * -s + y * c;

Que es exactamente lo que teníamos en nuestra muestra de rotación. Y, por último, la escala. Llamaremos a nuestros 2 factores de escala sx y sy y crearemos una matriz como esta

sx	0.0	0.0
0.0	sy	0.0
0.0	0.0	1.0

Si aplicamos la matriz, obtenemos lo siguiente:

newX = x * sx + y * 0 + 1 * 0

newY = x * 0 + y * sy + 1 * 0

extra = x * 0.0 + y * 0.0 + 1 * 1

que es realmente

newX = x * sx;
newY = y * sy;

Que es lo mismo que nuestro ejemplo de escalamiento. Ahora, sé que aún podrías estar pensando. ¿Y qué? ¿De qué sirve? ¿Parece mucho trabajo solo para hacer lo mismo que ya estábamos haciendo? Aquí es donde ocurre la magia. Resulta que podemos multiplicar matrices y aplicar todas las transformaciones a la vez. Supongamos que tenemos la función matrixMultiply, que toma dos matrices, las multiplica y muestra el resultado. Para que todo sea más claro, hagamos funciones para crear matrices de traslación, rotación y escala.

function makeTranslation(tx, ty) {
  return [
    1, 0, 0,
    0, 1, 0,
    tx, ty, 1
  ];
}

function makeRotation(angleInRadians) {
  var c = Math.cos(angleInRadians);
  var s = Math.sin(angleInRadians);
  return [
    c,-s, 0,
    s, c, 0,
    0, 0, 1
  ];
}

function makeScale(sx, sy) {
  return [
    sx, 0, 0,
    0, sy, 0,
    0, 0, 1
  ];
}

Ahora cambiemos nuestro sombreador. El sombreador anterior se veía de la siguiente manera:

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;
uniform vec2 u_scale;

void main() {
  // Scale the positon
  vec2 scaledPosition = a_position * u_scale;

  // Rotate the position
  vec2 rotatedPosition = vec2(
     scaledPosition.x * u_rotation.y + scaledPosition.y * u_rotation.x,
     scaledPosition.y * u_rotation.y - scaledPosition.x * u_rotation.x);

  // Add in the translation.
  vec2 position = rotatedPosition + u_translation;
  ...

Nuestro nuevo sombreador será mucho más simple.

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform mat3 u_matrix;

void main() {
  // Multiply the position by the matrix.
  vec2 position = (u_matrix * vec3(a_position, 1)).xy;
  ...

Y así es como lo usamos

  // Draw the scene.
  function drawScene() {
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Compute the matrices
    var translationMatrix =
       makeTranslation(translation[0], translation[1]);
    var rotationMatrix = makeRotation(angleInRadians);
    var scaleMatrix = makeScale(scale[0], scale[1]);

    // Multiply the matrices.
    var matrix = matrixMultiply(scaleMatrix, rotationMatrix);
    matrix = matrixMultiply(matrix, translationMatrix);

    // Set the matrix.
    gl.uniformMatrix3fv(matrixLocation, false, matrix);

    // Draw the rectangle.
    gl.drawArrays(gl.TRIANGLES, 0, 18);
  }

Sin embargo, es posible que te preguntes: ¿Y qué? No parece ser un gran beneficio . Sin embargo, ahora, si queremos cambiar el orden, no tenemos que escribir un sombreador nuevo. Solo podemos cambiar los cálculos.

    ...
    // Multiply the matrices.
    var matrix = matrixMultiply(translationMatrix, rotationMatrix);
    matrix = matrixMultiply(matrix, scaleMatrix);
    ...

Poder aplicar matrices como esta es especialmente importante para la animación jerárquica, como brazos en un cuerpo, lunas en un planeta alrededor de un sol o ramas en un árbol. Para ver un ejemplo sencillo de animación jerárquica, dibujemos nuestra "F" 5 veces, pero cada vez comencemos con la matriz de la "F" anterior.

  // Draw the scene.
  function drawScene() {
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Compute the matrices
    var translationMatrix = makeTranslation(translation[0], translation[1]);
    var rotationMatrix = makeRotation(angleInRadians);
    var scaleMatrix = makeScale(scale[0], scale[1]);

    // Starting Matrix.
    var matrix = makeIdentity();

    for (var i = 0; i < 5; ++i) {
      // Multiply the matrices.
      matrix = matrixMultiply(matrix, scaleMatrix);
      matrix = matrixMultiply(matrix, rotationMatrix);
      matrix = matrixMultiply(matrix, translationMatrix);

      // Set the matrix.
      gl.uniformMatrix3fv(matrixLocation, false, matrix);

      // Draw the geometry.
      gl.drawArrays(gl.TRIANGLES, 0, 18);
    }
  }

Para ello, presentamos la función makeIdentity, que crea una matriz de identidad. Una matriz de identidad es una matriz que representa de manera efectiva 1.0, de modo que, si la multiplicas por la identidad, no sucede nada. Al igual que

X * 1 = X

también

matrixX * identity = matrixX

Este es el código para crear una matriz de identidad.

function makeIdentity() {
  return [
    1, 0, 0,
    0, 1, 0,
    0, 0, 1
  ];
}

Otro ejemplo: En todos los ejemplos hasta ahora, nuestra "F" rota alrededor de su esquina superior izquierda. Esto se debe a que las matemáticas que usamos siempre giran alrededor del origen y la esquina superior izquierda de nuestra "F" está en el origen, (0, 0). Ahora, como podemos hacer cálculos de matrices y elegir el orden en que se aplican las transformaciones, podemos mover el origen antes de que se aplique el resto de las transformaciones.

    // make a matrix that will move the origin of the 'F' to
    // its center.
    var moveOriginMatrix = makeTranslation(-50, -75);
    ...

    // Multiply the matrices.
    var matrix = matrixMultiply(moveOriginMatrix, scaleMatrix);
    matrix = matrixMultiply(matrix, rotationMatrix);
    matrix = matrixMultiply(matrix, translationMatrix);

Con esa técnica, puedes rotar o escalar desde cualquier punto. Ahora sabes cómo Photoshop o Flash te permiten mover el punto de rotación. Vayamos aún más allá. Si vuelves al primer artículo sobre los conceptos básicos de WebGL, es posible que recuerdes que tenemos código en el sombreador para convertir de píxeles a espacio de recorte que se ve de la siguiente manera.

  ...
  // convert the rectangle from pixels to 0.0 to 1.0
  vec2 zeroToOne = position / u_resolution;

  // convert from 0->1 to 0->2
  vec2 zeroToTwo = zeroToOne * 2.0;

  // convert from 0->2 to -1->+1 (clipspace)
  vec2 clipSpace = zeroToTwo - 1.0;

  gl_Position = vec4(clipSpace * vec2(1, -1), 0, 1);

Si observas cada uno de esos pasos, el primero, "convertir de píxeles a 0.0 a 1.0", es realmente una operación de escala. La segunda también es una operación de escalamiento. El siguiente es un desplazamiento y el último escala Y en -1. De hecho, podemos hacer todo eso en la matriz que pasamos al sombreador. Podríamos crear 2 matrices de escala, una para escalar por 1.0/resolución, otra para escalar por 2.0, una tercera para traducir por -1.0, -1.0 y una cuarta para escalar Y por -1 y, luego, multiplicarlas todas, pero, en cambio, como las matemáticas son simples, solo crearemos una función que cree una matriz de "proyección" para una resolución determinada directamente.

function make2DProjection(width, height) {
  // Note: This matrix flips the Y axis so that 0 is at the top.
  return [
    2 / width, 0, 0,
    0, -2 / height, 0,
    -1, 1, 1
  ];
}

Ahora podemos simplificar aún más el sombreador. Este es el nuevo sombreador de vértices completo.

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform mat3 u_matrix;

void main() {
  // Multiply the position by the matrix.
  gl_Position = vec4((u_matrix * vec3(a_position, 1)).xy, 0, 1);
}
</script>

Y en JavaScript, debemos multiplicar por la matriz de proyección.

  // Draw the scene.
  function drawScene() {
    ...
    // Compute the matrices
    var projectionMatrix =
       make2DProjection(canvas.width, canvas.height);
    ...

    // Multiply the matrices.
    var matrix = matrixMultiply(scaleMatrix, rotationMatrix);
    matrix = matrixMultiply(matrix, translationMatrix);
    matrix = matrixMultiply(matrix, projectionMatrix);
    ...
  }

También quitamos el código que configuraba la resolución. Con este último paso, pasamos de un sombreador bastante complicado con 6 o 7 pasos a uno muy simple con solo 1 paso, todo gracias a la magia de las matemáticas matriciales.

Espero que este artículo haya ayudado a desmitificar las matemáticas de matrices. A continuación, pasaré al 3D. En las matrices 3D, las matemáticas siguen los mismos principios y usos. Comencé con 2D para que sea fácil de entender.