Bu sayfa, Cloud Translation API ile çevrilmiştir.

WebGL dönüşümleri

Gregg Tavares

WebGL 2D Çeviri

3D'ye geçmeden önce biraz daha 2D'de kalalım. Lütfen bekleyin. Bu makale bazılarına çok açık gelebilir ancak birkaç makalede bir noktaya değineceğim.

Bu makale, WebGL Temel Bilgileri ile başlayan bir serinin devamı niteliğindedir. Henüz okumadıysanız en azından ilk bölümü okuyup buraya geri dönmenizi öneririm. Çeviri, temelde bir şeyi "taşımak" anlamına gelen süslü bir matematik terimidir. Bir cümleyi İngilizceden Japoncaya taşımak da bu kapsamda değerlendirilebilir ancak bu durumda geometriyi taşımaktan bahsediyoruz. İlk yayında elde ettiğimiz örnek kodu kullanarak, setRectangle işlevine iletilen değerleri değiştirerek dikdörtgenimizi kolayca çevirebilirdiniz, değil mi? Önceki örneğimize dayalı bir örnek aşağıda verilmiştir.

  // First lets make some variables 
  // to hold the translation of the rectangle
  var translation = [0, 0];
  // then let's make a function to
  // re-draw everything. We can call this
  // function after we update the translation.
  // Draw the scene.
  function drawScene() {
     // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);
    // Setup a rectangle
    setRectangle(gl, translation[0], translation[1], width, height);

    // Draw the rectangle.
    gl.drawArrays(gl.TRIANGLES, 0, 6);
  }

Şu ana kadar her şey yolunda. Şimdi aynı işlemi daha karmaşık bir şekilde yapmak istediğimizi varsayalım. Bu gibi 6 üçgenden oluşan bir "F" çizmek istediğimizi varsayalım.

Mevcut kod şu şekilde. setRectangle işlevini aşağıdaki gibi bir işlevle değiştirmemiz gerekiyor.

// Fill the buffer with the values that define a letter 'F'.
function setGeometry(gl, x, y) {
  var width = 100;
  var height = 150;
  var thickness = 30;
  gl.bufferData(
      gl.ARRAY_BUFFER,
      new Float32Array([
          // left column
          x, y,
          x + thickness, y,
          x, y + height,
          x, y + height,
          x + thickness, y,
          x + thickness, y + height,

          // top rung
          x + thickness, y,
          x + width, y,
          x + thickness, y + thickness,
          x + thickness, y + thickness,
          x + width, y,
          x + width, y + thickness,

          // middle rung
          x + thickness, y + thickness * 2,
          x + width * 2 / 3, y + thickness * 2,
          x + thickness, y + thickness * 3,
          x + thickness, y + thickness * 3,
          x + width * 2 / 3, y + thickness * 2,
          x + width * 2 / 3, y + thickness * 3]),
      gl.STATIC_DRAW);
}

Bu yöntemin ölçeklenebilir olmadığını anlamışsınızdır. Yüzlerce veya binlerce satırdan oluşan çok karmaşık bir geometri çizmek istersek oldukça karmaşık bir kod yazmamız gerekir. Ayrıca, her çizim yaptığımızda JavaScript'in tüm noktaları güncellemesi gerekir. Daha basit bir yol var. Geometriyi yüklemeniz ve çeviriyi gölgelendiricide yapmanız yeterlidir. Yeni gölgelendirici

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform vec2 u_translation;

void main() {
   // Add in the translation.
   vec2 position = a_position + u_translation;

   // convert the rectangle from pixels to 0.0 to 1.0
   vec2 zeroToOne = position / u_resolution;
   ...

ve kodu biraz yeniden yapılandıracağız. Örneğin, geometriyi yalnızca bir kez ayarlamamız gerekir.

// Fill the buffer with the values that define a letter 'F'.
function setGeometry(gl) {
  gl.bufferData(
      gl.ARRAY_BUFFER,
      new Float32Array([
          // left column
          0, 0,
          30, 0,
          0, 150,
          0, 150,
          30, 0,
          30, 150,

          // top rung
          30, 0,
          100, 0,
          30, 30,
          30, 30,
          100, 0,
          100, 30,

          // middle rung
          30, 60,
          67, 60,
          30, 90,
          30, 90,
          67, 60,
          67, 90]),
      gl.STATIC_DRAW);
}

Ardından, istediğimiz çeviriyi kullanarak çizim yapmadan önce u_translation dosyasını güncellememiz yeterlidir.

  ...
  var translationLocation = gl.getUniformLocation(
             program, "u_translation");
  ...
  // Set Geometry.
  setGeometry(gl);
  ..
  // Draw scene.
  function drawScene() {
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Set the translation.
    gl.uniform2fv(translationLocation, translation);

    // Draw the rectangle.
    gl.drawArrays(gl.TRIANGLES, 0, 18);
  }

setGeometry işlevinin yalnızca bir kez çağrıldığını unutmayın. Artık drawScene içinde değil.

Artık çizim yaparken neredeyse her şeyi WebGL yapıyor. Tek yapmamız gereken bir çeviri ayarlamak ve çizmesini istemek. Geometrimizde on binlerce nokta olsa bile ana kod aynı kalır.

WebGL 2D Döndürme

Bunu nasıl açıklayacağımın mantıklı olup olmayacağını bilmiyorum ama denemeye değer.

Öncelikle sizi "birim çember" ile tanıştırmak istiyorum. Ortaokuldaki matematik derslerini hatırlıyorsanız (uyuyup uyanmayın!) bir dairenin yarıçapı olduğunu bilirsiniz. Bir dairenin yarıçapı, dairenin merkezinden kenara olan mesafedir. Birim daire, yarıçapı 1,0 olan bir dairedir.

3. sınıf matematik derslerinden hatırlarsanız bir sayıyı 1 ile çarparsanız sayı değişmez. Yani 123 * 1 = 123. Oldukça basit, değil mi? Bir birim daire, yarıçapı 1, 0 olan bir daire de 1'in bir şeklidir. Dönen bir 1. Bir sayıyı bu birim çemberle çarpabilirsiniz. Bu işlem, 1 ile çarpma işlemine benzer. Ancak burada sihirli bir şey olur ve öğeler döner. Bu X ve Y değerini birim çemberdeki herhangi bir noktadan alacağız ve geometrimizi önceki örneğimizdeki bu değerlerle çarpacağız. Gölgelendiricimizde yapılan güncellemeleri aşağıda bulabilirsiniz.

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;

void main() {
  // Rotate the position
  vec2 rotatedPosition = vec2(
     a_position.x * u_rotation.y + a_position.y * u_rotation.x,
     a_position.y * u_rotation.y - a_position.x * u_rotation.x);

  // Add in the translation.
  vec2 position = rotatedPosition + u_translation;

JavaScript'i, bu 2 değeri iletebileceğimiz şekilde güncelliyoruz.

  ...
  var rotationLocation = gl.getUniformLocation(program, "u_rotation");
  ...
  var rotation = [0, 1];
  ..
  // Draw the scene.
  function drawScene() {
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Set the translation.
    gl.uniform2fv(translationLocation, translation);

    // Set the rotation.
    gl.uniform2fv(rotationLocation, rotation);

    // Draw the rectangle.
    gl.drawArrays(gl.TRIANGLES, 0, 18);
  }

Neden işe yarar? Hesaplara bakalım.

rotatedX = a_position.x * u_rotation.y + a_position.y * u_rotation.x;
rotatedY = a_position.y * u_rotation.y - a_position.x * u_rotation.x;

Bir dikdörtgeniniz olduğunu ve bunu döndürmek istediğinizi varsayalım. Döndürmeye başlamadan önce sağ üst köşe 3,0; 9,0 konumundadır. Birim çemberde 12'den saat yönünde 30 derecelik bir nokta seçelim.

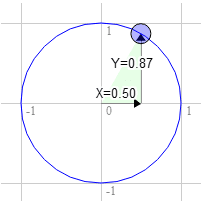
Çemberdeki konum 0,50 ve 0,87'dir.

3.0 * 0.87 + 9.0 * 0.50 = 7.1
9.0 * 0.87 - 3.0 * 0.50 = 6.3

Tam da olması gereken yerde

Saat yönünde 60 derece için de aynıdır.

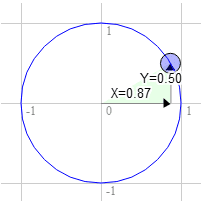
Çemberdeki konum 0,87 ve 0,50'dir.

3.0 * 0.50 + 9.0 * 0.87 = 9.3
9.0 * 0.50 - 3.0 * 0.87 = 1.9

Bu noktayı saat yönünde sağa döndürdüğümüzde X değerinin büyüdüğünü ve Y değerinin küçüldüğünü görebilirsiniz. 90 derecenin ötesine geçerseniz X tekrar küçülür ve Y büyür. Bu desen bize rotasyon sağlar. Birim çemberdeki noktaların başka bir adı vardır. Bunlara sinüs ve kosinüs denir. Dolayısıyla, herhangi bir açı için sinüs ve kosinüsü bu şekilde arayabiliriz.

function printSineAndCosineForAnAngle(angleInDegrees) {
  var angleInRadians = angleInDegrees * Math.PI / 180;
  var s = Math.sin(angleInRadians);
  var c = Math.cos(angleInRadians);
  console.log("s = " + s + " c = " + c);
}

Kodu kopyalayıp JavaScript konsolunuza yapıştırır ve printSineAndCosignForAngle(30) yazarsanız s = 0.49 c= 0.87 yazdırıldığını görürsünüz (not: Sayıları yuvarladım). Tüm bunları bir araya getirirseniz geometrinizi istediğiniz açıya döndürebilirsiniz. Döndürme işlemini, döndürmek istediğiniz açının sinüsü ve kosinüsü olarak ayarlamak yeterlidir.

  ...
  var angleInRadians = angleInDegrees * Math.PI / 180;
  rotation[0] = Math.sin(angleInRadians);
  rotation[1] = Math.cos(angleInRadians);

Bu açıklamanın işinize yarayacağını umuyorum. Şimdi daha basit bir örnek vereceğiz. Ölçeklendirin.

Radyan nedir?

Radyan, daireler, dönme ve açılarla kullanılan bir ölçü birimidir. Mesafeyi inç, yarda, metre vb. cinsinden ölçebildiğimiz gibi açıları da derece veya radyan cinsinden ölçebiliriz.

Metrik ölçümlerin kullanıldığı matematik işlemlerinin, İngiliz ölçümlerinin kullanıldığı matematik işlemlerinden daha kolay olduğunu muhtemelen biliyorsunuzdur. İnçten metreye geçmek için 12'ye böleriz. İnçleri yardalara dönüştürmek için 36'ya böleriz. Seni bilmem ama ben kafamda 36'ya bölemem. Metriklerle bu çok daha kolaydır. Milimetreyi santimetreye dönüştürmek için 10'a böleriz. Milimetreyi metreye çevirmek için 1000'e böleriz. Kafamda 1.000'e bölme işlemini yapabilirim.

Radyan ve derece benzerdir. Derecelendirmeler, matematiksel hesaplamayı zorlaştırır. Radyan, matematiği kolaylaştırır. Bir dairede 360 derece vardır ancak yalnızca 2π radyan vardır. Yani tam bir tur 2π radyan. Yarım tur π radyandır. 1/4 tur (90 derece) π/2 radyandır. Bir öğeyi 90 derece döndürmek istiyorsanız Math.PI * 0.5 simgesini kullanın. 45 derece döndürmek için Math.PI * 0.25 vb. kullanın.

Radyan cinsinden düşünmeye başladığınızda açı, daire veya dönme içeren neredeyse tüm matematik işlemleri çok basit bir şekilde yapılır. Bu yüzden denemeye ne dersiniz? Kullanıcı arayüzü ekranları dışında derece yerine radyan kullanın.

WebGL 2D Ölçek

Ölçeklendirme, çeviri kadar kolaydır.

Konumu, istediğimiz ölçekle çarparız. Önceki örneğimizdeki değişiklikleri aşağıda bulabilirsiniz.

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;
uniform vec2 u_scale;

void main() {
  // Scale the positon
  vec2 scaledPosition = a_position * u_scale;

  // Rotate the position
  vec2 rotatedPosition = vec2(
     scaledPosition.x * u_rotation.y +
        scaledPosition.y * u_rotation.x,
     scaledPosition.y * u_rotation.y -
        scaledPosition.x * u_rotation.x);

  // Add in the translation.
  vec2 position = rotatedPosition + u_translation;

ve çizerken ölçeği ayarlamak için gereken JavaScript'i ekleriz.

  ...
  var scaleLocation = gl.getUniformLocation(program, "u_scale");
  ...
  var scale = [1, 1];
  ...
  // Draw the scene.
  function drawScene() {
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Set the translation.
    gl.uniform2fv(translationLocation, translation);

    // Set the rotation.
    gl.uniform2fv(rotationLocation, rotation);

    // Set the scale.
    gl.uniform2fv(scaleLocation, scale);

    // Draw the rectangle.
    gl.drawArrays(gl.TRIANGLES, 0, 18);
  }

Negatif bir değerle ölçeklendirmenin geometrimizi tersine çevirdiğini unutmayın. Bu son 3 bölümün, kaydırma, döndürme ve ölçeklendirmeyi anlamanıza yardımcı olduğunu umuyoruz. Ardından, bunların üçünü de çok daha basit ve genellikle daha kullanışlı bir biçimde birleştiren matrislerin sihrini inceleyeceğiz.

Neden "F"?

"F" harfini ilk kez bir dokuda gördüm. "F"nin kendisi önemli değildir. Önemli olan, herhangi bir yönden bakıldığında cihazın yönünü anlayabilmenizdir. Örneğin, kalp ♥ veya üçgen △ kullansaydık yatay olarak çevrilip çevrilmediğini anlayamazdık. Daire ○ daha da kötü olur. Renkli bir dikdörtgenin her köşesinde farklı renkler kullanabilirsiniz ancak bu durumda hangi köşenin hangi renk olduğunu hatırlamanız gerekir. F harfi hemen tanınabilir.

Yönünü belirleyebileceğiniz herhangi bir şekil kullanılabilir. Ben, bu fikirle ilk tanıştığımdan beri "F" harfini kullanıyorum.

WebGL 2D Matrisleri

Son 3 bölümde geometrinin nasıl çevrileceğini, döndürüleceğini ve ölçeklendirileceğini ele aldık. Hareket ettirme, döndürme ve ölçek, her biri bir "dönüşüm" türü olarak kabul edilir. Bu dönüşümlerin her biri için gölgelendiricide değişiklik yapılması gerekiyordu ve 3 dönüşümün her biri sıraya bağlıydı.

Örneğin, burada 2, 1 ölçeği, %30 döndürme ve 100, 0 kaydırma değerleri verilmiştir.

Burada ise 100,0 hareket ettirme, %30 döndürme ve 2, 1 ölçek değerleri verilmiştir.

Sonuçlar tamamen farklıdır. Daha da kötüsü, ikinci örneğe ihtiyacımız olursa kaydırma, döndürme ve ölçeği yeni istediğimiz sırada uygulayan farklı bir gölgelendirici yazmamız gerekir. Benden çok daha zeki bazı insanlar, matris matematiğinde de aynı işlemleri yapabileceğinizi fark etti. 2D için 3x3 matris kullanırız. 3x3 matris, 9 kutu içeren bir ızgara gibidir.

1,0	2,0	3,0
4.0	5,0	6,0
7,0	8.0	9.0

Hesaplama yapmak için matrisin sütunlarındaki konumu çarpar ve sonuçları toplarız. Konumlarımızın yalnızca 2 değeri (x ve y) vardır ancak bu hesaplamayı yapmak için 3 değere ihtiyacımız vardır. Bu nedenle üçüncü değer olarak 1 değerini kullanacağız. Bu durumda sonucumuz

newX = x * 1.0 + y * 4.0 + 1 * 7.0

newY = x * 2.0 + y * 5.0 + 1 * 8.0

extra = x * 3.0 + y * 6.0 + 1 * 9.0

Muhtemelen buraya bakıyor ve "NE ANLAMI VAR?" diye düşünüyorsunuz. Bir çevirimiz olduğunu varsayalım. Çevirmek istediğimiz tutarı tx ve ty olarak adlandıracağız. Böyle bir matris oluşturalım

1,0	0,0	0,0
0,0	1,0	0,0
tx	ty	1,0

Şimdi de

newX = x * 1.0 + y * 0.0 + 1 * tx

newY = x * 0.0 + y * 1.0 + 1 * ty

extra = x * 0.0 + y * 0.0 + 1 * 1

Cebir bilginizi hatırlarsanız sıfırla çarpılan tüm yerleri silebiliriz. 1 ile çarpmak hiçbir şey yapmaz. Bu nedenle, ne olduğunu görmek için basitleştirelim.

newX = x + tx;
newY = y + ty;

Ek ücretler ise bizim için çok önemli değil. Bu kod, çeviri örneğimizdeki çeviri koduna şaşırtıcı bir şekilde benziyor. Benzer şekilde, rotasyon yapalım. Döndürme konulu makalede de belirttiğimiz gibi, döndürmek istediğimiz açının sinüsü ve kosinüsü bize yeterlidir.

s = Math.sin(angleToRotateInRadians);
c = Math.cos(angleToRotateInRadians);

Ve böyle bir matris oluşturuyoruz

c	-s	0,0
s	c	0,0
0,0	0,0	1,0

Matrisi uyguladığımızda şunu elde ederiz:

newX = x * c + y * s + 1 * 0

newY = x * -s + y * c + 1 * 0

extra = x * 0.0 + y * 0.0 + 1 * 1

Tümünü 0 ve 1 ile çarpıp siyahlaştırdığımızda şunu elde ederiz:

newX = x *  c + y * s;
newY = x * -s + y * c;

Tam da rotasyon örneğimizde olduğu gibi. Son olarak ölçek. 2 ölçek faktörümüzü sx ve sy olarak adlandıracağız. Bu şekilde bir matris oluşturuyoruz.

sx	0,0	0,0
0,0	sy	0,0
0,0	0,0	1,0

Matrisi uyguladığımızda şunu elde ederiz:

newX = x * sx + y * 0 + 1 * 0

newY = x * 0 + y * sy + 1 * 0

extra = x * 0.0 + y * 0.0 + 1 * 1

Bu gerçekten de

newX = x * sx;
newY = y * sy;

Bu, ölçeklendirme örneğimizle aynıdır. Eminim hâlâ düşünüyorsunuzdur. Peki bu durumda ne olur? Anlaşılması gereken bir nokta da bu. Bu, zaten yaptığımız şeyi yapmak için çok fazla iş gibi görünüyor. İşte burada sihre rastlarız. Matrisleri çarpıp tüm dönüşümleri aynı anda uygulayabileceğimizi görüyoruz. İki matrisi alan, çarpan ve sonucu döndüren matrixMultiply işlevimiz olduğunu varsayalım. Konuyu daha net hale getirmek için çeviri, döndürme ve ölçek için matrisler oluşturacak işlevler oluşturalım.

function makeTranslation(tx, ty) {
  return [
    1, 0, 0,
    0, 1, 0,
    tx, ty, 1
  ];
}

function makeRotation(angleInRadians) {
  var c = Math.cos(angleInRadians);
  var s = Math.sin(angleInRadians);
  return [
    c,-s, 0,
    s, c, 0,
    0, 0, 1
  ];
}

function makeScale(sx, sy) {
  return [
    sx, 0, 0,
    0, sy, 0,
    0, 0, 1
  ];
}

Şimdi gölgelendiricimizi değiştirelim. Eski gölgelendirici şöyle görünüyordu

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;
uniform vec2 u_scale;

void main() {
  // Scale the positon
  vec2 scaledPosition = a_position * u_scale;

  // Rotate the position
  vec2 rotatedPosition = vec2(
     scaledPosition.x * u_rotation.y + scaledPosition.y * u_rotation.x,
     scaledPosition.y * u_rotation.y - scaledPosition.x * u_rotation.x);

  // Add in the translation.
  vec2 position = rotatedPosition + u_translation;
  ...

Yeni gölgelendiricimiz çok daha basit olacak.

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform mat3 u_matrix;

void main() {
  // Multiply the position by the matrix.
  vec2 position = (u_matrix * vec3(a_position, 1)).xy;
  ...

Bu özelliği nasıl kullandığımızı

  // Draw the scene.
  function drawScene() {
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Compute the matrices
    var translationMatrix =
       makeTranslation(translation[0], translation[1]);
    var rotationMatrix = makeRotation(angleInRadians);
    var scaleMatrix = makeScale(scale[0], scale[1]);

    // Multiply the matrices.
    var matrix = matrixMultiply(scaleMatrix, rotationMatrix);
    matrix = matrixMultiply(matrix, translationMatrix);

    // Set the matrix.
    gl.uniformMatrix3fv(matrixLocation, false, matrix);

    // Draw the rectangle.
    gl.drawArrays(gl.TRIANGLES, 0, 18);
  }

Peki bu durum ne anlama geliyor? Bu pek avantajlı bir durum değil . Ancak artık sırayı değiştirmek istediğimizde yeni bir gölgelendirici yazmak zorunda değiliz. Hesaplamayı değiştirebiliriz.

    ...
    // Multiply the matrices.
    var matrix = matrixMultiply(translationMatrix, rotationMatrix);
    matrix = matrixMultiply(matrix, scaleMatrix);
    ...

Bu tür matrisleri uygulayabilmek, özellikle bir vücuttaki kollar, bir gezegenin etrafındaki aylar veya bir ağaçtaki dallar gibi hiyerarşik animasyonlar için önemlidir. Hiyerarşik animasyonla ilgili basit bir örnek olarak "F"mizi 5 kez çizelim ancak her seferinde önceki "F"nin matrisiyle başlayalım.

  // Draw the scene.
  function drawScene() {
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Compute the matrices
    var translationMatrix = makeTranslation(translation[0], translation[1]);
    var rotationMatrix = makeRotation(angleInRadians);
    var scaleMatrix = makeScale(scale[0], scale[1]);

    // Starting Matrix.
    var matrix = makeIdentity();

    for (var i = 0; i < 5; ++i) {
      // Multiply the matrices.
      matrix = matrixMultiply(matrix, scaleMatrix);
      matrix = matrixMultiply(matrix, rotationMatrix);
      matrix = matrixMultiply(matrix, translationMatrix);

      // Set the matrix.
      gl.uniformMatrix3fv(matrixLocation, false, matrix);

      // Draw the geometry.
      gl.drawArrays(gl.TRIANGLES, 0, 18);
    }
  }

Bunun için kimlik matrisi oluşturan makeIdentity işlevini kullanıma sunduk. Kimlik matrisi, 1,0 değerini etkili bir şekilde temsil eden bir matristir.Bu nedenle, kimlikle çarptığınızda hiçbir şey olmaz.

X * 1 = X

ben de

matrixX * identity = matrixX

Kimlik matrisi oluşturmak için kullanabileceğiniz kod aşağıda verilmiştir.

function makeIdentity() {
  return [
    1, 0, 0,
    0, 1, 0,
    0, 0, 1
  ];
}

Bir örnek daha vereyim. Şimdiye kadarki her örnekte "F" harfi sol üst köşesi etrafında dönüyor. Bunun nedeni, kullandığımız matematiğin her zaman orijin etrafında dönmesi ve "F"mizin sol üst köşesinin orijinde (0, 0) olmasıdır. Ancak artık matris matematiği yapabildiğimiz ve dönüşümlerin uygulanma sırasını seçebildiğimiz için dönüşümlerin geri kalanı uygulanmadan önce orijini taşıyabiliriz.

    // make a matrix that will move the origin of the 'F' to
    // its center.
    var moveOriginMatrix = makeTranslation(-50, -75);
    ...

    // Multiply the matrices.
    var matrix = matrixMultiply(moveOriginMatrix, scaleMatrix);
    matrix = matrixMultiply(matrix, rotationMatrix);
    matrix = matrixMultiply(matrix, translationMatrix);

Bu tekniği kullanarak herhangi bir noktadan döndürme veya ölçeklendirme yapabilirsiniz. Photoshop veya Flash'ın, döndürme noktasını nasıl taşıyabileceğinizi öğrendiniz. Daha da çılgın bir şey yapalım. WebGL temelleri ile ilgili ilk makaleye geri dönerseniz gölgelendiricide pikselleri kırpma alanına dönüştürmek için aşağıdaki gibi bir kodumuz olduğunu hatırlayabilirsiniz.

  ...
  // convert the rectangle from pixels to 0.0 to 1.0
  vec2 zeroToOne = position / u_resolution;

  // convert from 0->1 to 0->2
  vec2 zeroToTwo = zeroToOne * 2.0;

  // convert from 0->2 to -1->+1 (clipspace)
  vec2 clipSpace = zeroToTwo - 1.0;

  gl_Position = vec4(clipSpace * vec2(1, -1), 0, 1);

Bu adımların her birine sırayla bakarsanız ilk adım olan "pikselleri 0,0 ile 1,0 arasında dönüştürme" aslında bir ölçekleme işlemidir. İkinci işlem de ölçeklendirme işlemidir. Sonraki bir çeviridir ve en son ifade Y değerini -1 ile ölçeklendirir. Aslında tüm bunları, gölgelendiriciye aktardığımız matriste yapabiliriz. Biri 1,0/çözünürlük, diğeri 2,0, üçüncüsü -1,0, -1,0 ve dördüncüsü Y'yi -1 ile ölçeklendirecek 2 ölçek matrisi oluşturabilir ve ardından hepsini birlikte çarpabiliriz. Ancak matematik basit olduğu için doğrudan belirli bir çözünürlük için "projeksiyon" matrisi oluşturan bir işlev oluşturacağız.

function make2DProjection(width, height) {
  // Note: This matrix flips the Y axis so that 0 is at the top.
  return [
    2 / width, 0, 0,
    0, -2 / height, 0,
    -1, 1, 1
  ];
}

Şimdi gölgelendiriciyi daha da basitleştirebiliriz. Yeni köşe düğümü gölgelendiricisinin tamamı aşağıda verilmiştir.

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform mat3 u_matrix;

void main() {
  // Multiply the position by the matrix.
  gl_Position = vec4((u_matrix * vec3(a_position, 1)).xy, 0, 1);
}
</script>

JavaScript'te ise projeksiyon matrisiyle çarpmamız gerekir.

  // Draw the scene.
  function drawScene() {
    ...
    // Compute the matrices
    var projectionMatrix =
       make2DProjection(canvas.width, canvas.height);
    ...

    // Multiply the matrices.
    var matrix = matrixMultiply(scaleMatrix, rotationMatrix);
    matrix = matrixMultiply(matrix, translationMatrix);
    matrix = matrixMultiply(matrix, projectionMatrix);
    ...
  }

Çözünürlüğü ayarlayan kodu da kaldırdık. Bu son adımla, matris matematiğinin büyüsü sayesinde 6-7 adımlı oldukça karmaşık bir gölgelendiriciden yalnızca 1 adımlı çok basit bir gölgelendiriciye geçtik.

Bu makalenin, matris matematiğinin anlaşılmasına yardımcı olduğunu umuyoruz. Ardından 3D'ye geçeceğim. 3D matrislerde matematik aynı ilkeler ve kullanıma sahiptir. Anlaşılması kolay olması için 2D ile başladım.