Halaman ini diterjemahkan oleh Cloud Translation API.

Transformasi WebGL

Gregg Tavares

Terjemahan 2D WebGL

Sebelum beralih ke 3D, mari kita tetap menggunakan 2D untuk sementara waktu. Harap bersabar. Artikel ini mungkin tampak sangat jelas bagi sebagian orang, tetapi saya akan menjelaskannya secara bertahap dalam beberapa artikel.

Artikel ini adalah kelanjutan dari seri yang dimulai dengan Dasar-Dasar WebGL. Jika belum membacanya, sebaiknya baca setidaknya bab pertama, lalu kembali ke sini. Terjemahan adalah nama matematika yang rumit yang pada dasarnya berarti "memindahkan" sesuatu. Saya kira memindahkan kalimat dari bahasa Inggris ke bahasa Jepang juga cocok, tetapi dalam hal ini kita berbicara tentang memindahkan geometri. Dengan menggunakan kode contoh yang kita dapatkan di postingan pertama, Anda dapat menerjemahkan persegi panjang dengan mudah hanya dengan mengubah nilai yang diteruskan ke setRectangle, bukan? Berikut adalah contoh berdasarkan contoh sebelumnya.

  // First lets make some variables 
  // to hold the translation of the rectangle
  var translation = [0, 0];
  // then let's make a function to
  // re-draw everything. We can call this
  // function after we update the translation.
  // Draw the scene.
  function drawScene() {
     // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);
    // Setup a rectangle
    setRectangle(gl, translation[0], translation[1], width, height);

    // Draw the rectangle.
    gl.drawArrays(gl.TRIANGLES, 0, 6);
  }

Sejauh ini tidak ada masalah. Namun, sekarang bayangkan kita ingin melakukan hal yang sama dengan bentuk yang lebih rumit. Misalkan kita ingin menggambar 'F' yang terdiri dari 6 segitiga seperti ini.

Nah, berikut adalah kode saat ini yang harus kita ubah setRectangle menjadi sesuatu yang lebih seperti ini.

// Fill the buffer with the values that define a letter 'F'.
function setGeometry(gl, x, y) {
  var width = 100;
  var height = 150;
  var thickness = 30;
  gl.bufferData(
      gl.ARRAY_BUFFER,
      new Float32Array([
          // left column
          x, y,
          x + thickness, y,
          x, y + height,
          x, y + height,
          x + thickness, y,
          x + thickness, y + height,

          // top rung
          x + thickness, y,
          x + width, y,
          x + thickness, y + thickness,
          x + thickness, y + thickness,
          x + width, y,
          x + width, y + thickness,

          // middle rung
          x + thickness, y + thickness * 2,
          x + width * 2 / 3, y + thickness * 2,
          x + thickness, y + thickness * 3,
          x + thickness, y + thickness * 3,
          x + width * 2 / 3, y + thickness * 2,
          x + width * 2 / 3, y + thickness * 3]),
      gl.STATIC_DRAW);
}

Anda mungkin dapat melihat bahwa hal ini tidak akan diskalakan dengan baik. Jika ingin menggambar beberapa geometri yang sangat kompleks dengan ratusan atau ribuan garis, kita harus menulis beberapa kode yang cukup kompleks. Selain itu, setiap kali kita menggambar, JavaScript harus memperbarui semua titik. Ada cara yang lebih sederhana. Cukup upload geometri dan lakukan terjemahan di shader. Berikut shader barunya

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform vec2 u_translation;

void main() {
   // Add in the translation.
   vec2 position = a_position + u_translation;

   // convert the rectangle from pixels to 0.0 to 1.0
   vec2 zeroToOne = position / u_resolution;
   ...

dan kita akan menyusun ulang kode sedikit. Pertama, kita hanya perlu menetapkan geometri satu kali.

// Fill the buffer with the values that define a letter 'F'.
function setGeometry(gl) {
  gl.bufferData(
      gl.ARRAY_BUFFER,
      new Float32Array([
          // left column
          0, 0,
          30, 0,
          0, 150,
          0, 150,
          30, 0,
          30, 150,

          // top rung
          30, 0,
          100, 0,
          30, 30,
          30, 30,
          100, 0,
          100, 30,

          // middle rung
          30, 60,
          67, 60,
          30, 90,
          30, 90,
          67, 60,
          67, 90]),
      gl.STATIC_DRAW);
}

Kemudian, kita hanya perlu memperbarui u_translation sebelum menggambar dengan terjemahan yang kita inginkan.

  ...
  var translationLocation = gl.getUniformLocation(
             program, "u_translation");
  ...
  // Set Geometry.
  setGeometry(gl);
  ..
  // Draw scene.
  function drawScene() {
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Set the translation.
    gl.uniform2fv(translationLocation, translation);

    // Draw the rectangle.
    gl.drawArrays(gl.TRIANGLES, 0, 18);
  }

Perhatikan bahwa setGeometry hanya dipanggil satu kali. Tidak lagi berada di dalam drawScene.

Sekarang saat kita menggambar, WebGL hampir melakukan semuanya. Yang kita lakukan hanyalah menyetel terjemahan dan memintanya untuk menggambar. Meskipun geometri kita memiliki puluhan ribu titik, kode utamanya akan tetap sama.

Rotasi 2D WebGL

Saya harus mengakui bahwa saya tidak tahu apakah cara saya menjelaskan ini akan masuk akal, tetapi apa pun, sebaiknya coba saja.

Pertama, saya ingin memperkenalkan apa yang disebut "lingkaran unit". Jika Anda ingat pelajaran matematika SMP (jangan tidur!), lingkaran memiliki jari-jari. Radius lingkaran adalah jarak dari pusat lingkaran ke tepi. Lingkaran unit adalah lingkaran dengan radius 1,0.

Jika Anda ingat dari matematika dasar kelas 3, jika Anda mengalikan sesuatu dengan 1, hasilnya akan tetap sama. Jadi, 123 * 1 = 123. Cukup sederhana, bukan? Lingkaran unit, lingkaran dengan radius 1, 0 juga merupakan bentuk dari 1. Ini adalah angka 1 yang berputar. Jadi, Anda dapat mengalikan sesuatu dengan lingkaran unit ini dan pada dasarnya seperti mengalikan dengan 1, kecuali jika terjadi keajaiban dan semuanya berputar. Kita akan mengambil nilai X dan Y tersebut dari titik mana pun pada lingkaran unit dan kita akan mengalikan geometri dengan nilai tersebut dari contoh sebelumnya. Berikut adalah update pada shader kami.

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;

void main() {
  // Rotate the position
  vec2 rotatedPosition = vec2(
     a_position.x * u_rotation.y + a_position.y * u_rotation.x,
     a_position.y * u_rotation.y - a_position.x * u_rotation.x);

  // Add in the translation.
  vec2 position = rotatedPosition + u_translation;

Dan kita memperbarui JavaScript agar dapat meneruskan 2 nilai tersebut.

  ...
  var rotationLocation = gl.getUniformLocation(program, "u_rotation");
  ...
  var rotation = [0, 1];
  ..
  // Draw the scene.
  function drawScene() {
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Set the translation.
    gl.uniform2fv(translationLocation, translation);

    // Set the rotation.
    gl.uniform2fv(rotationLocation, rotation);

    // Draw the rectangle.
    gl.drawArrays(gl.TRIANGLES, 0, 18);
  }

Mengapa cara ini berhasil? Nah, lihat hitungannya.

rotatedX = a_position.x * u_rotation.y + a_position.y * u_rotation.x;
rotatedY = a_position.y * u_rotation.y - a_position.x * u_rotation.x;

Misalnya, Anda memiliki persegi panjang dan ingin memutarnya. Sebelum Anda mulai memutarnya, pojok kanan atas berada di 3.0, 9.0. Mari kita pilih titik pada lingkaran unit 30 derajat searah jarum jam dari jam 12.

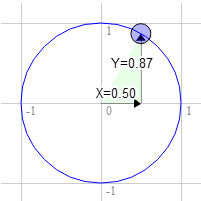
Posisi pada lingkaran adalah 0,50 dan 0,87

3.0 * 0.87 + 9.0 * 0.50 = 7.1
9.0 * 0.87 - 3.0 * 0.50 = 6.3

Itulah tempat yang tepat untuknya

Hal yang sama berlaku untuk 60 derajat searah jarum jam

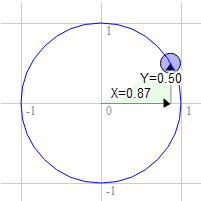
Posisi pada lingkaran adalah 0,87 dan 0,50

3.0 * 0.50 + 9.0 * 0.87 = 9.3
9.0 * 0.50 - 3.0 * 0.87 = 1.9

Anda dapat melihat bahwa saat kita memutar titik tersebut searah jarum jam ke kanan, nilai X akan bertambah besar dan nilai Y akan berkurang. Jika terus melewati 90 derajat, X akan mulai mengecil lagi dan Y akan mulai membesar. Pola tersebut memberi kita rotasi. Ada nama lain untuk titik pada lingkaran unit. Fungsi ini disebut sinus dan kosinus. Jadi, untuk sudut tertentu, kita cukup mencari sinus dan kosinus seperti ini.

function printSineAndCosineForAnAngle(angleInDegrees) {
  var angleInRadians = angleInDegrees * Math.PI / 180;
  var s = Math.sin(angleInRadians);
  var c = Math.cos(angleInRadians);
  console.log("s = " + s + " c = " + c);
}

Jika Anda menyalin dan menempelkan kode ke konsol JavaScript dan mengetik printSineAndCosignForAngle(30), Anda akan melihatnya mencetak s = 0.49 c= 0.87 (catatan: Saya membulatkan angka). Jika menggabungkan semuanya, Anda dapat memutar geometri ke sudut yang diinginkan. Cukup tetapkan rotasi ke sinus dan kosinus sudut yang ingin Anda putar.

  ...
  var angleInRadians = angleInDegrees * Math.PI / 180;
  rotation[0] = Math.sin(angleInRadians);
  rotation[1] = Math.cos(angleInRadians);

Semoga informasi ini bermanfaat. Berikutnya, yang lebih sederhana. Skalakan.

Apa yang dimaksud dengan radian?

Radian adalah satuan pengukuran yang digunakan dengan lingkaran, rotasi, dan sudut. Sama seperti kita dapat mengukur jarak dalam inci, yard, meter, dll., kita dapat mengukur sudut dalam derajat atau radian.

Anda mungkin menyadari bahwa matematika dengan pengukuran metrik lebih mudah daripada matematika dengan pengukuran imperial. Untuk mengubah inci menjadi kaki, kita bagi dengan 12. Untuk mengubah inci menjadi yard, kita bagi dengan 36. Saya tidak tahu bagaimana dengan Anda, tetapi saya tidak dapat membagi dengan 36 dalam pikiran saya. Dengan metrik, prosesnya jauh lebih mudah. Untuk mengubah milimeter menjadi sentimeter, kita bagi dengan 10. Untuk mengubah milimeter menjadi meter, kita bagi dengan 1.000. Saya dapat membagi dengan 1.000 di dalam kepala.

Radian vs derajat serupa. Derajat membuat matematika menjadi sulit. Radian mempermudah penghitungan. Ada 360 derajat dalam lingkaran, tetapi hanya ada 2π radian. Jadi, satu putaran penuh adalah 2π radian. Setengah putaran adalah π radian. 1/4 putaran, yaitu 90 derajat adalah π/2 radian. Jadi, jika Anda ingin memutar sesuatu 90 derajat, cukup gunakan Math.PI * 0.5. Jika Anda ingin memutarnya 45 derajat, gunakan Math.PI * 0.25, dll.

Hampir semua matematika yang melibatkan sudut, lingkaran, atau rotasi berfungsi dengan sangat sederhana jika Anda mulai berpikir dalam satuan radian. Jadi, cobalah. Gunakan radian, bukan derajat, kecuali dalam tampilan UI.

Skala 2D WebGL

Penskalaan sama mudahnya dengan penerjemahan.

Kita mengalikan posisi dengan skala yang diinginkan. Berikut adalah perubahan dari contoh sebelumnya.

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;
uniform vec2 u_scale;

void main() {
  // Scale the positon
  vec2 scaledPosition = a_position * u_scale;

  // Rotate the position
  vec2 rotatedPosition = vec2(
     scaledPosition.x * u_rotation.y +
        scaledPosition.y * u_rotation.x,
     scaledPosition.y * u_rotation.y -
        scaledPosition.x * u_rotation.x);

  // Add in the translation.
  vec2 position = rotatedPosition + u_translation;

dan kita menambahkan JavaScript yang diperlukan untuk menetapkan skala saat menggambar.

  ...
  var scaleLocation = gl.getUniformLocation(program, "u_scale");
  ...
  var scale = [1, 1];
  ...
  // Draw the scene.
  function drawScene() {
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Set the translation.
    gl.uniform2fv(translationLocation, translation);

    // Set the rotation.
    gl.uniform2fv(rotationLocation, rotation);

    // Set the scale.
    gl.uniform2fv(scaleLocation, scale);

    // Draw the rectangle.
    gl.drawArrays(gl.TRIANGLES, 0, 18);
  }

Satu hal yang perlu diperhatikan adalah penskalaan dengan nilai negatif akan membalik geometri kita. Semoga 3 bab terakhir ini membantu Anda memahami translasi, rotasi, dan skala. Selanjutnya, kita akan membahas keajaiban matriks yang menggabungkan ketiga hal ini menjadi bentuk yang jauh lebih sederhana dan sering kali lebih berguna.

Mengapa 'F'?

Pertama kali saya melihat seseorang menggunakan 'F' adalah pada tekstur. 'F' itu sendiri tidak penting. Yang penting adalah Anda dapat mengetahui orientasinya dari arah mana pun. Misalnya, jika kita menggunakan hati ♥ atau segitiga △, kita tidak dapat mengetahui apakah simbol tersebut dibalik secara horizontal. Lingkaran ○ akan lebih buruk lagi. Persegi panjang berwarna mungkin akan berfungsi dengan warna yang berbeda di setiap sudut, tetapi Anda harus mengingat sudut mana yang mana. Orientasi F langsung dapat dikenali.

Bentuk apa pun yang dapat Anda identifikasi orientasinya akan berfungsi. Saya baru saja menggunakan 'F' sejak saya 'F'irst diperkenalkan dengan ide ini.

Matriks 2D WebGL

Dalam 3 bab terakhir, kita telah membahas cara menerjemahkan geometri, memutar geometri, dan menskalakan geometri. Translasi, rotasi, dan skala masing-masing dianggap sebagai jenis 'transformasi'. Setiap transformasi ini memerlukan perubahan pada shader dan setiap 3 transformasi bergantung pada urutan.

Misalnya, berikut adalah skala 2, 1, rotasi 30%, dan terjemahan 100, 0.

Berikut adalah translasi 100,0, rotasi 30%, dan skala 2, 1

Hasilnya benar-benar berbeda. Lebih buruk lagi, jika kita memerlukan contoh kedua, kita harus menulis shader lain yang menerapkan terjemahan, rotasi, dan skala dalam urutan baru yang diinginkan. Nah, beberapa orang yang jauh lebih pintar dari saya, menemukan bahwa Anda dapat melakukan semua hal yang sama dengan matematika matriks. Untuk 2d, kita menggunakan matriks 3x3. Matriks 3x3 seperti petak dengan 9 kotak.

1.0	2.0	3.0
4.0	5,0	6.0
7,0	8.0	9.0

Untuk melakukan penghitungan, kita mengalikan posisi di kolom matriks dan menambahkan hasilnya. Posisi kita hanya memiliki 2 nilai, x dan y, tetapi untuk melakukan matematika ini, kita memerlukan 3 nilai sehingga kita akan menggunakan 1 untuk nilai ketiga. dalam hal ini, hasilnya adalah

newX = x * 1.0 + y * 4.0 + 1 * 7.0

newY = x * 2.0 + y * 5.0 + 1 * 8.0

extra = x * 3.0 + y * 6.0 + 1 * 9.0

Anda mungkin melihatnya dan berpikir "APA FAEDAHNYA". Baiklah, mari kita asumsikan kita memiliki terjemahan. Kita akan memanggil jumlah yang ingin diterjemahkan tx dan ty. Mari kita buat matriks seperti ini

1.0	0,0	0.0
0,0	1,0	0,0
tx	ty	1.0

Sekarang, mari kita lihat

newX = x * 1.0 + y * 0.0 + 1 * tx

newY = x * 0.0 + y * 1.0 + 1 * ty

extra = x * 0.0 + y * 0.0 + 1 * 1

Jika Anda ingat aljabar, kita dapat menghapus tempat yang dikalikan dengan nol. Mengalikan dengan 1 secara efektif tidak melakukan apa pun, jadi mari kita sederhanakan untuk melihat apa yang terjadi

newX = x + tx;
newY = y + ty;

Dan tambahan yang tidak terlalu penting bagi kita. Kode tersebut terlihat seperti kode terjemahan dari contoh terjemahan kita. Demikian pula, mari kita lakukan rotasi. Seperti yang telah kita tunjukkan dalam postingan rotasi, kita hanya memerlukan sinus dan cosinus sudut yang ingin kita putar.

s = Math.sin(angleToRotateInRadians);
c = Math.cos(angleToRotateInRadians);

Dan kita membuat matriks seperti ini

c	-s	0,0
s	c	0,0
0.0	0,0	1.0

Dengan menerapkan matriks, kita mendapatkan

newX = x * c + y * s + 1 * 0

newY = x * -s + y * c + 1 * 0

extra = x * 0.0 + y * 0.0 + 1 * 1

Dengan mengaburkan semua perkalian dengan 0 dan 1, kita mendapatkan

newX = x *  c + y * s;
newY = x * -s + y * c;

Ini persis seperti yang kita miliki dalam contoh rotasi. Dan terakhir, skala. Kita akan menyebut 2 faktor skala kita sx dan sy Lalu kita membuat matriks seperti ini

sx	0,0	0.0
0,0	sy	0,0
0.0	0,0	1.0

Dengan menerapkan matriks, kita mendapatkan

newX = x * sx + y * 0 + 1 * 0

newY = x * 0 + y * sy + 1 * 0

extra = x * 0.0 + y * 0.0 + 1 * 1

yang benar-benar

newX = x * sx;
newY = y * sy;

Yang sama dengan contoh penskalaan kami. Sekarang, saya yakin Anda mungkin masih berpikir. Jadi bagaimana? Apa maksudnya. Kedengarannya banyak pekerjaan yang harus dilakukan hanya untuk melakukan hal yang sama seperti yang sudah kita lakukan? Di sinilah keajaiban terjadi. Ternyata kita dapat mengalikan matriks dan menerapkan semua transformasi sekaligus. Anggaplah kita memiliki fungsi, matrixMultiply, yang menggunakan dua matriks, mengalikan keduanya, dan menampilkan hasilnya. Untuk memperjelasnya, mari kita buat fungsi untuk membuat matriks untuk terjemahan, rotasi, dan skala.

function makeTranslation(tx, ty) {
  return [
    1, 0, 0,
    0, 1, 0,
    tx, ty, 1
  ];
}

function makeRotation(angleInRadians) {
  var c = Math.cos(angleInRadians);
  var s = Math.sin(angleInRadians);
  return [
    c,-s, 0,
    s, c, 0,
    0, 0, 1
  ];
}

function makeScale(sx, sy) {
  return [
    sx, 0, 0,
    0, sy, 0,
    0, 0, 1
  ];
}

Sekarang, mari kita ubah shader. Shader lama terlihat seperti ini

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;
uniform vec2 u_scale;

void main() {
  // Scale the positon
  vec2 scaledPosition = a_position * u_scale;

  // Rotate the position
  vec2 rotatedPosition = vec2(
     scaledPosition.x * u_rotation.y + scaledPosition.y * u_rotation.x,
     scaledPosition.y * u_rotation.y - scaledPosition.x * u_rotation.x);

  // Add in the translation.
  vec2 position = rotatedPosition + u_translation;
  ...

Shader baru kita akan jauh lebih sederhana.

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform mat3 u_matrix;

void main() {
  // Multiply the position by the matrix.
  vec2 position = (u_matrix * vec3(a_position, 1)).xy;
  ...

Dan berikut cara menggunakannya

  // Draw the scene.
  function drawScene() {
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Compute the matrices
    var translationMatrix =
       makeTranslation(translation[0], translation[1]);
    var rotationMatrix = makeRotation(angleInRadians);
    var scaleMatrix = makeScale(scale[0], scale[1]);

    // Multiply the matrices.
    var matrix = matrixMultiply(scaleMatrix, rotationMatrix);
    matrix = matrixMultiply(matrix, translationMatrix);

    // Set the matrix.
    gl.uniformMatrix3fv(matrixLocation, false, matrix);

    // Draw the rectangle.
    gl.drawArrays(gl.TRIANGLES, 0, 18);
  }

Namun, Anda mungkin bertanya, lalu apa? Sepertinya tidak banyak manfaatnya . Namun, sekarang jika kita ingin mengubah urutan, kita tidak perlu menulis shader baru. Kita cukup mengubah rumusnya.

    ...
    // Multiply the matrices.
    var matrix = matrixMultiply(translationMatrix, rotationMatrix);
    matrix = matrixMultiply(matrix, scaleMatrix);
    ...

Kemampuan untuk menerapkan matriks seperti ini sangat penting untuk animasi hierarkis seperti lengan pada tubuh, bulan di planet di sekitar matahari, atau cabang di pohon. Untuk contoh sederhana animasi hierarkis, mari kita gambar 'F' sebanyak 5 kali, tetapi setiap kali kita mulai dengan matriks dari 'F' sebelumnya.

  // Draw the scene.
  function drawScene() {
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Compute the matrices
    var translationMatrix = makeTranslation(translation[0], translation[1]);
    var rotationMatrix = makeRotation(angleInRadians);
    var scaleMatrix = makeScale(scale[0], scale[1]);

    // Starting Matrix.
    var matrix = makeIdentity();

    for (var i = 0; i < 5; ++i) {
      // Multiply the matrices.
      matrix = matrixMultiply(matrix, scaleMatrix);
      matrix = matrixMultiply(matrix, rotationMatrix);
      matrix = matrixMultiply(matrix, translationMatrix);

      // Set the matrix.
      gl.uniformMatrix3fv(matrixLocation, false, matrix);

      // Draw the geometry.
      gl.drawArrays(gl.TRIANGLES, 0, 18);
    }
  }

Untuk melakukannya, kita telah memperkenalkan fungsi, makeIdentity, yang membuat matriks identitas. Matriks identitas adalah matriks yang secara efektif mewakili 1,0 sehingga jika Anda mengalikan dengan identitas, tidak akan terjadi apa pun. Sama seperti

X * 1 = X

juga

matrixX * identity = matrixX

Berikut adalah kode untuk membuat matriks identitas.

function makeIdentity() {
  return [
    1, 0, 0,
    0, 1, 0,
    0, 0, 1
  ];
}

Satu contoh lagi, Dalam setiap sampel sejauh ini, 'F' kita berputar di sekitar sudut kiri atas. Hal ini karena matematika yang kita gunakan selalu berputar di sekitar asal dan sudut kiri atas 'F' kita berada di asal, (0, 0) Tetapi sekarang, karena kita dapat melakukan matematika matriks dan kita dapat memilih urutan transformasi diterapkan, kita dapat memindahkan asal sebelum transformasi lainnya diterapkan.

    // make a matrix that will move the origin of the 'F' to
    // its center.
    var moveOriginMatrix = makeTranslation(-50, -75);
    ...

    // Multiply the matrices.
    var matrix = matrixMultiply(moveOriginMatrix, scaleMatrix);
    matrix = matrixMultiply(matrix, rotationMatrix);
    matrix = matrixMultiply(matrix, translationMatrix);

Dengan teknik tersebut, Anda dapat memutar atau menskalakan dari titik mana pun. Sekarang Anda tahu cara Photoshop atau Flash memungkinkan Anda memindahkan titik rotasi. Mari kita lakukan hal yang lebih gila. Jika kembali ke artikel pertama tentang dasar-dasar WebGL, Anda mungkin ingat bahwa kita memiliki kode dalam shader untuk mengonversi dari piksel ke ruang klip yang terlihat seperti ini.

  ...
  // convert the rectangle from pixels to 0.0 to 1.0
  vec2 zeroToOne = position / u_resolution;

  // convert from 0->1 to 0->2
  vec2 zeroToTwo = zeroToOne * 2.0;

  // convert from 0->2 to -1->+1 (clipspace)
  vec2 clipSpace = zeroToTwo - 1.0;

  gl_Position = vec4(clipSpace * vec2(1, -1), 0, 1);

Jika Anda melihat setiap langkah tersebut secara bergantian, langkah pertama, "konversi dari piksel ke 0,0 hingga 1,0", sebenarnya adalah operasi penskalaan. Yang kedua juga merupakan operasi penskalaan. Yang berikutnya adalah terjemahan dan yang terakhir menskalakan Y sebesar -1. Kita sebenarnya dapat melakukannya semua dalam matriks yang kita teruskan ke shader. Kita dapat membuat 2 matriks skala, satu untuk diskalakan dengan 1,0/resolusi, yang lain untuk diskalakan dengan 2,0, yang ketiga untuk diterjemahkan dengan -1,0,-1,0, dan yang keempat untuk menskalakan Y dengan -1, lalu mengalikan semuanya, tetapi karena matematikanya sederhana, kita hanya akan membuat fungsi yang membuat matriks 'proyeksi' untuk resolusi tertentu secara langsung.

function make2DProjection(width, height) {
  // Note: This matrix flips the Y axis so that 0 is at the top.
  return [
    2 / width, 0, 0,
    0, -2 / height, 0,
    -1, 1, 1
  ];
}

Sekarang kita dapat menyederhanakan shader lebih lanjut. Berikut adalah seluruh shader vertex baru.

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform mat3 u_matrix;

void main() {
  // Multiply the position by the matrix.
  gl_Position = vec4((u_matrix * vec3(a_position, 1)).xy, 0, 1);
}
</script>

Dan di JavaScript, kita perlu mengalikan dengan matriks proyeksi

  // Draw the scene.
  function drawScene() {
    ...
    // Compute the matrices
    var projectionMatrix =
       make2DProjection(canvas.width, canvas.height);
    ...

    // Multiply the matrices.
    var matrix = matrixMultiply(scaleMatrix, rotationMatrix);
    matrix = matrixMultiply(matrix, translationMatrix);
    matrix = matrixMultiply(matrix, projectionMatrix);
    ...
  }

Kami juga menghapus kode yang menetapkan resolusi. Dengan langkah terakhir ini, kita telah beralih dari shader yang agak rumit dengan 6-7 langkah menjadi shader yang sangat sederhana dengan hanya 1 langkah yang dilakukan oleh keajaiban matematika matriks.

Semoga artikel ini telah membantu menjelaskan matematika matriks. Selanjutnya, saya akan beralih ke 3D. Dalam matriks 3D, matematika mengikuti prinsip dan penggunaan yang sama. Saya memulai dengan 2D agar mudah dipahami.