การเปลี่ยนรูปแบบ WebGL

การแปล WebGL 2 มิติ

ก่อนที่จะไปต่อกันที่ 3 มิติ เรามาลองใช้แบบ 2 มิติกันอีกสักครู่ อดทนกับฉันหน่อย บทความนี้อาจฟังดูชัดเจนเกินไปสำหรับบางคน แต่เราจะเพิ่มข้อมูลจนถึงจุดนี้ในบทความ 2-3 บทความ

บทความนี้มีเนื้อหาต่อเนื่องมาจากซีรีส์ที่เริ่มต้นด้วยพื้นฐาน WebGL หากยังไม่ได้อ่าน เราขอแนะนำให้อ่านอย่างน้อย 1 บทแล้วกลับมาที่นี่ คำแปลเป็นชื่อทางคณิตศาสตร์ที่จำง่าย ซึ่งแปลว่า "ย้าย" บางสิ่ง ผมคิดว่าควรย้ายประโยคจากภาษาอังกฤษเป็นภาษาญี่ปุ่นได้พอดี แต่ในกรณีนี้เรากำลังพูดถึงการย้ายเรขาคณิต เมื่อใช้โค้ดตัวอย่างที่เราเขียนลงในโพสต์แรก คุณก็จะแปลรูปสี่เหลี่ยมผืนผ้าของเราได้ง่ายๆ ด้วยการเปลี่ยนค่าที่ส่งไปยัง setRectangle ใช่ไหม นี่คือตัวอย่างที่อิงจากตัวอย่างก่อนหน้านี้

  // First lets make some variables 
  // to hold the translation of the rectangle
  var translation = [0, 0];
  // then let's make a function to
  // re-draw everything. We can call this
  // function after we update the translation.
  // Draw the scene.
  function drawScene() {
     // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);
    // Setup a rectangle
    setRectangle(gl, translation[0], translation[1], width, height);

    // Draw the rectangle.
    gl.drawArrays(gl.TRIANGLES, 0, 6);
  }

จนถึงตอนนี้ แต่ตอนนี้ลองคิดดูว่าเราต้องการทำแบบเดียวกันนี้กับรูปร่างที่ซับซ้อนมากขึ้น สมมติว่าเราอยากวาด 'F' ที่มีรูปสามเหลี่ยม 6 รูปแบบนี้

ต่อไปนี้เป็นโค้ดปัจจุบันที่เราต้องเปลี่ยน setRectangle ให้เป็นแบบนี้

// Fill the buffer with the values that define a letter 'F'.
function setGeometry(gl, x, y) {
  var width = 100;
  var height = 150;
  var thickness = 30;
  gl.bufferData(
      gl.ARRAY_BUFFER,
      new Float32Array([
          // left column
          x, y,
          x + thickness, y,
          x, y + height,
          x, y + height,
          x + thickness, y,
          x + thickness, y + height,

          // top rung
          x + thickness, y,
          x + width, y,
          x + thickness, y + thickness,
          x + thickness, y + thickness,
          x + width, y,
          x + width, y + thickness,

          // middle rung
          x + thickness, y + thickness * 2,
          x + width * 2 / 3, y + thickness * 2,
          x + thickness, y + thickness * 3,
          x + thickness, y + thickness * 3,
          x + width * 2 / 3, y + thickness * 2,
          x + width * 2 / 3, y + thickness * 3]),
      gl.STATIC_DRAW);
}

เราหวังว่าคุณคงเข้าใจได้ไม่ดีเท่าไหร่ ถ้าเราต้องการวาดรูปเรขาคณิตที่ซับซ้อนมากที่มีเส้นเป็นร้อยเป็นพันเส้น เราก็คงต้องเขียนโค้ดที่ซับซ้อนหน่อย ยิ่งไปกว่านั้น ทุกครั้งที่เราวาด JavaScript ต้องอัปเดตจุดทั้งหมดด้วย มีวิธีที่ง่ายกว่านี้ เพียงอัปโหลดเรขาคณิตและทำการแปลในเฉดสี นี่คือตัวปรับแสงเงาใหม่

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform vec2 u_translation;

void main() {
   // Add in the translation.
   vec2 position = a_position + u_translation;

   // convert the rectangle from pixels to 0.0 to 1.0
   vec2 zeroToOne = position / u_resolution;
   ...

และเราจะปรับโครงสร้างของโค้ดใหม่ สำหรับคนเราต้องกำหนดเรขาคณิตเพียงครั้งเดียว

// Fill the buffer with the values that define a letter 'F'.
function setGeometry(gl) {
  gl.bufferData(
      gl.ARRAY_BUFFER,
      new Float32Array([
          // left column
          0, 0,
          30, 0,
          0, 150,
          0, 150,
          30, 0,
          30, 150,

          // top rung
          30, 0,
          100, 0,
          30, 30,
          30, 30,
          100, 0,
          100, 30,

          // middle rung
          30, 60,
          67, 60,
          30, 90,
          30, 90,
          67, 60,
          67, 90]),
      gl.STATIC_DRAW);
}

จากนั้นเราจำเป็นต้องอัปเดต u_translation ก่อนที่จะร่างคำแปลตามที่ต้องการ

  ...
  var translationLocation = gl.getUniformLocation(
             program, "u_translation");
  ...
  // Set Geometry.
  setGeometry(gl);
  ..
  // Draw scene.
  function drawScene() {
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Set the translation.
    gl.uniform2fv(translationLocation, translation);

    // Draw the rectangle.
    gl.drawArrays(gl.TRIANGLES, 0, 18);
  }

สังเกตว่า setGeometry จะมีการเรียกเพียงครั้งเดียว แท็กไม่ได้อยู่ในDrawScene แล้ว

ตอนนี้เวลาที่เราวาด WebGL แทบจะทำอะไรไม่ได้เลย สิ่งที่เราทำคือการตั้งค่าคำแปลและขอให้วาด แม้ว่าเรขาคณิตของเราจะมีจุดนับหมื่นจุด แต่รหัสหลักจะยังคงเดิม

การหมุน 2 มิติของ WebGL

ฉันจะยอมรับตั้งแต่แรกเลยว่าไม่รู้เลยว่าฉันจะอธิบายเรื่องนี้อย่างไรจะฟังได้ แต่จะเกิดอะไรขึ้น

ก่อนอื่น เราอยากแนะนำให้คุณรู้จักกับสิ่งที่เรียกว่า "วงกลมหน่วย" หากคุณจำคณิตศาสตร์สมัยมัธยมต้นได้ (อย่าไปนอนทับฉันนะ!) วงกลมมีรัศมี รัศมีของวงกลมคือระยะทางจากจุดศูนย์กลางของวงกลมถึงขอบ วงกลม 1 หน่วยคือวงกลมที่มีรัศมี 1.0

ถ้าจำจากคณิตศาสตร์ชั้นประถมศึกษาปีที่ 3 เบื้องต้นได้ หากคูณบางอย่างด้วย 1 ค่านั้นก็จะเท่ากัน ดังนั้น 123 * 1 = 123 นี่เป็นเรื่องพื้นฐานใช่ไหม วงกลมหนึ่งหน่วยหรือวงกลมที่มีรัศมี 1.0 ก็ถือเป็น 1 เช่นกัน ตัวอักษรนี้เป็นเลข 1 แบบหมุน คุณจึงคูณบางอย่างกับวงกลมหนึ่งหน่วยนี้ ในลักษณะคล้ายกับการคูณด้วย 1 เว้นแต่ว่าเวทมนตร์จะเกิดขึ้นแล้วสิ่งต่างๆ จะหมุน เราจะนำค่า X และ Y จากจุดใดก็ได้ในวงกลมของหน่วยมาคูณเรขาคณิตกับตัวอย่างก่อนหน้านี้ การอัปเดตเฉดสีของเรามีดังนี้

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;

void main() {
  // Rotate the position
  vec2 rotatedPosition = vec2(
     a_position.x * u_rotation.y + a_position.y * u_rotation.x,
     a_position.y * u_rotation.y - a_position.x * u_rotation.x);

  // Add in the translation.
  vec2 position = rotatedPosition + u_translation;

แล้วอัปเดต JavaScript เพื่อให้ส่งค่า 2 ค่านั้นเข้ามาได้

  ...
  var rotationLocation = gl.getUniformLocation(program, "u_rotation");
  ...
  var rotation = [0, 1];
  ..
  // Draw the scene.
  function drawScene() {
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Set the translation.
    gl.uniform2fv(translationLocation, translation);

    // Set the rotation.
    gl.uniform2fv(rotationLocation, rotation);

    // Draw the rectangle.
    gl.drawArrays(gl.TRIANGLES, 0, 18);
  }

เหตุใดจึงได้ผล ลองคำนวณดูสิ

rotatedX = a_position.x * u_rotation.y + a_position.y * u_rotation.x;
rotatedY = a_position.y * u_rotation.y - a_position.x * u_rotation.x;

เป็นรูปสี่เหลี่ยมผืนผ้าและอยากหมุน ก่อนที่คุณจะเริ่มหมุน มุมขวาบนคือ 3.0, 9.0 ลองเลือกจุดบนวงกลมหนึ่งหน่วยจาก 12.00 น. ตามเข็มนาฬิกา

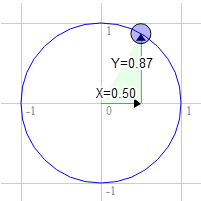
ตำแหน่งในวงกลมคือ 0.50 และ 0.87

3.0 * 0.87 + 9.0 * 0.50 = 7.1
9.0 * 0.87 - 3.0 * 0.50 = 6.3

และนั่นคือส่วนที่เราต้องการ

เหมือนกันสำหรับ 60 องศาตามเข็มนาฬิกา

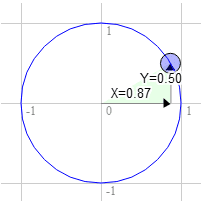
ตำแหน่งในวงกลมคือ 0.87 และ 0.50

3.0 * 0.50 + 9.0 * 0.87 = 9.3
9.0 * 0.50 - 3.0 * 0.87 = 1.9

คุณจะเห็นได้ว่าเมื่อเราหมุนจุดตามเข็มนาฬิกาไปทางขวา ค่า X จะใหญ่ขึ้นและ Y จะเล็กลง หากเลย 90 องศา X จะเริ่มเล็กลงอีกครั้งและ Y จะเริ่มใหญ่ขึ้น รูปแบบดังกล่าวจะทำให้เราหมุนเวียน จุดในวงกลมหนึ่งหน่วยมีอีกชื่อหนึ่ง เรียกว่าไซน์และโคไซน์ ดังนั้นไม่ว่าจะในมุมใดก็ตาม เราสามารถหาค่าไซน์และโคไซน์แบบนี้

function printSineAndCosineForAnAngle(angleInDegrees) {
  var angleInRadians = angleInDegrees * Math.PI / 180;
  var s = Math.sin(angleInRadians);
  var c = Math.cos(angleInRadians);
  console.log("s = " + s + " c = " + c);
}

หากคัดลอกและวางโค้ดลงในคอนโซล JavaScript แล้วพิมพ์ printSineAndCosignForAngle(30) คุณจะเห็นโค้ดพิมพ์ s = 0.49 c= 0.87 (หมายเหตุ: ฉันปัดเศษตัวเลขขึ้น) หากนำภาพทั้งหมดมาประกอบกัน คุณสามารถหมุนเรขาคณิตเป็นมุมใดก็ได้ตามต้องการ เพียงตั้งค่าการหมุนเป็นไซน์และโคไซน์ของมุมที่คุณต้องการหมุน

  ...
  var angleInRadians = angleInDegrees * Math.PI / 180;
  rotation[0] = Math.sin(angleInRadians);
  rotation[1] = Math.cos(angleInRadians);

เราหวังว่าคุณจะเข้าใจ ต่อไปเป็นเรื่องที่ง่ายกว่านี้ ปรับสเกล

เรเดียนคืออะไร

เรเดียนคือหน่วยวัดที่ใช้กับวงกลม การหมุน และมุม เราสามารถวัดมุมเป็นองศาหรือเรเดียนได้เช่นเดียวกับที่เราสามารถวัดระยะทางเป็นนิ้ว หลา เมตร ฯลฯ

คุณอาจทราบดีว่าคณิตศาสตร์ที่ใช้การวัดเมตริกนั้นง่ายกว่าคณิตศาสตร์ที่ใช้การวัดแบบอิมพีเรียล ถ้าจะให้ห่างจากนิ้วเป็นฟุต เราหารด้วย 12 ถ้าจะให้ห่างจากนิ้วเป็นหลา เราหารด้วย 36 ไม่รู้เรื่องเธอเลย แต่เอาแค่ 36 ในหัวไม่ได้ เมตริกจะง่ายขึ้นมาก ถ้าจะเปลี่ยนจากมิลลิเมตรเป็นเซนติเมตร เราหารด้วย 10 เราหาร 1,000 ตั้งแต่มิลลิเมตรถึงเมตร ฉันได้หารด้วย 1,000 ในหัว

เรเดียนกับองศาคล้ายกัน องศาทำให้คณิตศาสตร์ยาก เรเดียนช่วยแก้โจทย์ได้ง่ายๆ วงกลมมี 360 องศา แต่มีเรเดียนเพียง 2UPLOAD เท่านั้น ดังนั้นการเลี้ยวทั้งหมดคือ 2π เรเดียน การเลี้ยวครึ่งหนึ่งคือ ตั้งแต่ต้นเรเดียน เทิร์น 1/4 นั่นคือ 90 ดีกรีคือ ไปเลย/2 เรเดียน ดังนั้น หากคุณต้องการหมุนบางสิ่ง 90 องศา เพียงใช้ Math.PI * 0.5 หากคุณต้องการหมุน 45 องศา ให้ใช้ Math.PI * 0.25 เป็นต้น

การคำนวณเกือบทั้งหมดที่เกี่ยวข้องกับมุม วงกลม หรือการหมุนจะใช้การได้ง่ายๆ เมื่อคุณเริ่มคิดเป็นเรเดียน ลองใช้เลย ใช้เรเดียน ไม่ใช่องศายกเว้นในหน้าจอ UI

สเกล 2 มิติของ WebGL

การปรับขนาดนั้นง่ายพอๆ กับการแปลภาษา

เราคูณตำแหน่งด้วยสเกลที่ต้องการ ต่อไปนี้คือการเปลี่ยนแปลงจากตัวอย่างก่อนหน้านี้

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;
uniform vec2 u_scale;

void main() {
  // Scale the positon
  vec2 scaledPosition = a_position * u_scale;

  // Rotate the position
  vec2 rotatedPosition = vec2(
     scaledPosition.x * u_rotation.y +
        scaledPosition.y * u_rotation.x,
     scaledPosition.y * u_rotation.y -
        scaledPosition.x * u_rotation.x);

  // Add in the translation.
  vec2 position = rotatedPosition + u_translation;

แล้วเพิ่ม JavaScript ที่ต้องใช้ในการกำหนดขนาดเมื่อวาด

  ...
  var scaleLocation = gl.getUniformLocation(program, "u_scale");
  ...
  var scale = [1, 1];
  ...
  // Draw the scene.
  function drawScene() {
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Set the translation.
    gl.uniform2fv(translationLocation, translation);

    // Set the rotation.
    gl.uniform2fv(rotationLocation, rotation);

    // Set the scale.
    gl.uniform2fv(scaleLocation, scale);

    // Draw the rectangle.
    gl.drawArrays(gl.TRIANGLES, 0, 18);
  }

สิ่งหนึ่งที่ควรทราบคือการปรับขนาดโดยใช้ค่าลบจะเป็นการพลิกรูปทรงเรขาคณิตของเรา เราหวังว่า 3 บทสุดท้ายนี้จะช่วยให้คุณเข้าใจการแปล การหมุน และการปรับขนาด ต่อไปเราจะพูดถึงความมหัศจรรย์ซึ่งก็คือเมทริกซ์ที่รวม 3 เมตริกนี้เข้าด้วยกันในรูปแบบที่เรียบง่ายและมักจะมีประโยชน์มากกว่า

ทำไมต้องใช้ "F"

ครั้งแรกที่ฉันเห็นคนใช้ 'F' ที่พื้นผิว ตัว 'F' นั้นไม่สำคัญ สิ่งสำคัญคือคุณสามารถบอกแนวความคิดว่ามาจากทิศทางใดก็ได้ ตัวอย่างเช่น หากเราใช้หัวใจ ♥ หรือสามเหลี่ยม △ เราจะไม่สามารถบอกได้ว่าตัวเลขนั้นพลิกในแนวนอนหรือไม่ แวดวง ○ ยิ่งแย่ลงอีก สี่เหลี่ยมผืนผ้าสีน่าจะทำงานได้กับสีที่ต่างกันในแต่ละมุม แต่คุณต้องจำไว้ว่ามุมใดคือมุมใด แนวของ F จะจดจำได้ทันที

รูปร่างใดที่คุณบอกได้ว่าแนวไหนน่าจะใช้งานได้ ผมเพิ่งใช้ 'F' ตั้งแต่ที่ผมเป็น 'F'irst แนะนำแนวคิดนี้

เมทริกซ์ 2 มิติของ WebGL

ใน 3 บทที่ผ่านมา เราได้พูดถึงวิธีแปลเรขาคณิต หมุนเรขาคณิต และปรับขนาดเรขาคณิต การแปล การหมุน และการปรับขนาดต่างก็ถือว่าเป็น "การเปลี่ยนรูปแบบ" ประเภทหนึ่ง การเปลี่ยนรูปแบบแต่ละรายการเหล่านี้จำเป็นต้องมีการเปลี่ยนแปลงตัวปรับแสงเงา และการเปลี่ยนรูปแบบทั้ง 3 แบบขึ้นอยู่กับลำดับ

ตัวอย่างเช่น นี่เป็นสเกล 2, 1, การหมุน 30% และการแปลเป็น 100, 0

และนี่คือคำแปลของ 100,0, การหมุน 30% และมาตราส่วน 2, 1

ผลลัพธ์แตกต่างกันโดยสิ้นเชิง ยิ่งไปกว่านั้น หากเราต้องการตัวอย่างที่ 2 เราจำเป็นต้องเขียนตัวปรับแสงเงาที่แตกต่างกันซึ่งใช้การแปล การหมุน และการปรับขนาดในลำดับใหม่ที่ต้องการ บางคนฉลาดกว่าฉันมากเลย ถึงคุณจะรู้ว่าสามารถทำทุกอย่างเดียวกันได้ด้วยคณิตศาสตร์แบบเดอะเมทริกซ์ สำหรับแบบ 2 มิติ เราใช้เมทริกซ์ 3x3 เมทริกซ์ 3x3 เป็นเหมือนตารางกริดที่มี 9 กล่อง

1.0	2.0	3.0
4.0	5.0	6.0
7.0	8.0	9.0

ในการคำนวณ เราจะคูณตำแหน่งในคอลัมน์ของเมทริกซ์แล้วนำผลลัพธ์ที่ได้มาคูณกัน ตำแหน่งของเรามีเพียง 2 ค่า คือ x และ y แต่ในการคํานวณนี้ เราต้องใช้ 3 ค่า ดังนั้น เราจะใช้ 1 สําหรับค่าที่ 3 ในกรณีนี้ผลลัพธ์ของเราคือ

newX = x * 1.0 + y * 4.0 + 1 * 7.0

newY = x * 2.0 + y * 5.0 + 1 * 8.0

extra = x * 3.0 + y * 6.0 + 1 * 9.0

คุณอาจกำลังดูอยู่และคิดว่า "ประเด็นคืออะไร" สมมติว่าเรามีคำแปล เราจะเรียกจำนวนที่เราต้องการแปล tx และ ty มาสร้างเมทริกซ์แบบนี้กัน

1.0	0.0	0.0
0.0	1.0	0.0
tx	ty	1.0

ลองดูเลย

newX = x * 1.0 + y * 0.0 + 1 * tx

newY = x * 0.0 + y * 1.0 + 1 * ty

extra = x * 0.0 + y * 0.0 + 1 * 1

หากคุณจำพีชคณิตได้ เราจะลบตำแหน่งใดก็ได้ที่คูณด้วย 0 การคูณด้วย 1 อย่างมีประสิทธิภาพจะไม่ช่วยอะไรเลย ลองทำให้ง่ายขึ้นเพื่อดูว่าเกิดอะไรขึ้น

newX = x + tx;
newY = y + ty;

และเพิ่มเติมคือสิ่งที่เราไม่สนใจนัก รหัสดังกล่าวดูเหมือนโค้ดการแปลจากตัวอย่างการแปลของเราอย่างน่าประหลาด ลองใช้การหมุนเวียนแบบเดียวกัน เช่นเดียวกับที่เราระบุไว้ในโพสต์การหมุน เราเพียงต้องการไซน์และโคไซน์ของมุมที่เราต้องการหมุน

s = Math.sin(angleToRotateInRadians);
c = Math.cos(angleToRotateInRadians);

แล้วเราก็สร้างเมทริกซ์แบบนี้

c	-วิ	0.0
วินาที	c	0.0
0.0	0.0	1.0

ประยุกต์ใช้เมทริกซ์ที่เราได้รับ

newX = x * c + y * s + 1 * 0

newY = x * -s + y * c + 1 * 0

extra = x * 0.0 + y * 0.0 + 1 * 1

ซ่อนค่าทั้งหมดคูณด้วย 0 และ 1 เราจะได้ค่า

newX = x *  c + y * s;
newY = x * -s + y * c;

ซึ่งเป็นสิ่งที่เรามีในตัวอย่างการหมุนเวียนของเรา และขั้นตอนสุดท้าย เราจะเรียกตัวประกอบ 2 ขนาดว่า sx และ sy และสร้างเมทริกซ์แบบนี้

เซ็กซ์	0.0	0.0
0.0	Sys	0.0
0.0	0.0	1.0

ประยุกต์ใช้เมทริกซ์ที่เราได้รับ

newX = x * sx + y * 0 + 1 * 0

newY = x * 0 + y * sy + 1 * 0

extra = x * 0.0 + y * 0.0 + 1 * 1

ซึ่งจริงๆ แล้ว

newX = x * sx;
newY = y * sy;

ซึ่งจะเหมือนกับตัวอย่างการปรับขนาดของเรา ฉันแน่ใจว่าคุณอาจกำลังคิดอยู่ แล้วยังไงต่อ ประเด็นคือ ดูเหมือนว่าจะมีงานหนักเพื่อทำสิ่งเดิมๆ ที่เราทำอยู่แล้วใช่ไหม นี่คือจุดที่เวทมนตร์เข้ามามีบทบาท ผลที่ได้คือเราสามารถคูณเมทริกซ์เข้าด้วยกัน และใช้การแปลงทั้งหมดพร้อมกันได้ สมมติว่าเรามีฟังก์ชัน matrixMultiply ที่ใช้ 2 เมทริกซ์ นำไปคูณกับผลลัพธ์ เพื่อให้เข้าใจชัดเจนขึ้น เรามาสร้างเมทริกซ์สำหรับการแปล การหมุน และการปรับขนาดกัน

function makeTranslation(tx, ty) {
  return [
    1, 0, 0,
    0, 1, 0,
    tx, ty, 1
  ];
}

function makeRotation(angleInRadians) {
  var c = Math.cos(angleInRadians);
  var s = Math.sin(angleInRadians);
  return [
    c,-s, 0,
    s, c, 0,
    0, 0, 1
  ];
}

function makeScale(sx, sy) {
  return [
    sx, 0, 0,
    0, sy, 0,
    0, 0, 1
  ];
}

คราวนี้มาเปลี่ยนตัวปรับแสงเงากัน ตัวปรับแสงเงาตัวเก่ามีหน้าตาแบบนี้

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;
uniform vec2 u_scale;

void main() {
  // Scale the positon
  vec2 scaledPosition = a_position * u_scale;

  // Rotate the position
  vec2 rotatedPosition = vec2(
     scaledPosition.x * u_rotation.y + scaledPosition.y * u_rotation.x,
     scaledPosition.y * u_rotation.y - scaledPosition.x * u_rotation.x);

  // Add in the translation.
  vec2 position = rotatedPosition + u_translation;
  ...

ตัวปรับเฉดสีใหม่ของเราจะใช้งานง่ายขึ้นมาก

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform mat3 u_matrix;

void main() {
  // Multiply the position by the matrix.
  vec2 position = (u_matrix * vec3(a_position, 1)).xy;
  ...

และนี่คือวิธีที่เราใช้

  // Draw the scene.
  function drawScene() {
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Compute the matrices
    var translationMatrix =
       makeTranslation(translation[0], translation[1]);
    var rotationMatrix = makeRotation(angleInRadians);
    var scaleMatrix = makeScale(scale[0], scale[1]);

    // Multiply the matrices.
    var matrix = matrixMultiply(scaleMatrix, rotationMatrix);
    matrix = matrixMultiply(matrix, translationMatrix);

    // Set the matrix.
    gl.uniformMatrix3fv(matrixLocation, false, matrix);

    // Draw the rectangle.
    gl.drawArrays(gl.TRIANGLES, 0, 18);
  }

ถึงกระนั้น คุณอาจสงสัยว่า แล้วยังไงต่อ ฟังดูไม่มีประโยชน์มากนัก แต่ตอนนี้หากต้องการเปลี่ยนลำดับ เราก็ไม่ต้องเขียนตัวปรับเฉดสีใหม่ เราแค่เปลี่ยนสูตรคำนวณ

    ...
    // Multiply the matrices.
    var matrix = matrixMultiply(translationMatrix, rotationMatrix);
    matrix = matrixMultiply(matrix, scaleMatrix);
    ...

ความสามารถในการใช้เมทริกซ์เช่นนี้สำคัญอย่างยิ่งสำหรับภาพเคลื่อนไหวแบบลำดับชั้น เช่น แขนบนลำตัว ดวงจันทร์บนดาวเคราะห์ที่อยู่รอบดวงอาทิตย์ หรือกิ่งไม้บนต้นไม้ ตัวอย่างง่ายๆ ของภาพเคลื่อนไหวที่มีลำดับขั้นคือวาดรูป 'F' 5 ครั้งโดยแต่ละครั้งให้เริ่มด้วยเมทริกซ์จาก 'F' ก่อนหน้า

  // Draw the scene.
  function drawScene() {
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Compute the matrices
    var translationMatrix = makeTranslation(translation[0], translation[1]);
    var rotationMatrix = makeRotation(angleInRadians);
    var scaleMatrix = makeScale(scale[0], scale[1]);

    // Starting Matrix.
    var matrix = makeIdentity();

    for (var i = 0; i < 5; ++i) {
      // Multiply the matrices.
      matrix = matrixMultiply(matrix, scaleMatrix);
      matrix = matrixMultiply(matrix, rotationMatrix);
      matrix = matrixMultiply(matrix, translationMatrix);

      // Set the matrix.
      gl.uniformMatrix3fv(matrixLocation, false, matrix);

      // Draw the geometry.
      gl.drawArrays(gl.TRIANGLES, 0, 18);
    }
  }

ในการดำเนินการนี้ เราได้แนะนำฟังก์ชัน makeIdentity ซึ่งสร้างเมทริกซ์เอกลักษณ์ เมทริกซ์เอกลักษณ์คือเมทริกซ์ที่แสดงค่า 1.0 ได้อย่างมีประสิทธิภาพ ดังนั้นการคูณด้วยอัตลักษณ์จะไม่เกิดขึ้นเลย เหมือน

X * 1 = X

เช่นกัน

matrixX * identity = matrixX

นี่คือโค้ดสำหรับสร้างเมทริกซ์ข้อมูลประจำตัว

function makeIdentity() {
  return [
    1, 0, 0,
    0, 1, 0,
    0, 0, 1
  ];
}

อีกตัวอย่างหนึ่งคือ ในทุกๆ ตัวอย่าง จนถึงขณะนี้ 'F' หมุนวนบริเวณมุมซ้ายบน เนื่องจากการคำนวณที่เราใช้จะหมุนรอบจุดเริ่มต้นเสมอ และมุมซ้ายบนของเครื่องหมาย 'F' จะอยู่ที่จุดเริ่มต้น (0, 0) แต่ตอนนี้ เพราะเราสามารถทำคณิตศาสตร์เมทริกซ์ได้ และเราสามารถเลือกลำดับที่จะใช้การแปลงได้ เราจึงสามารถย้ายจุดเริ่มต้นก่อนนำการแปลงที่เหลือไปใช้

    // make a matrix that will move the origin of the 'F' to
    // its center.
    var moveOriginMatrix = makeTranslation(-50, -75);
    ...

    // Multiply the matrices.
    var matrix = matrixMultiply(moveOriginMatrix, scaleMatrix);
    matrix = matrixMultiply(matrix, rotationMatrix);
    matrix = matrixMultiply(matrix, translationMatrix);

คุณสามารถใช้เทคนิคดังกล่าวเพื่อหมุนหรือปรับขนาดจากจุดใดก็ได้ ตอนนี้คุณก็ทราบวิธีที่ Photoshop หรือ Flash ช่วยในการย้ายจุดหมุนแล้ว สนุกให้เต็มที่ไปอีก หากกลับไปที่บทความแรกเกี่ยวกับข้อมูลพื้นฐานของ WebGL คุณอาจจำได้ว่าเรามีโค้ดในตัวปรับสีให้แปลงจากพิกเซลเป็น Clipspace ที่มีหน้าตาแบบนี้

  ...
  // convert the rectangle from pixels to 0.0 to 1.0
  vec2 zeroToOne = position / u_resolution;

  // convert from 0->1 to 0->2
  vec2 zeroToTwo = zeroToOne * 2.0;

  // convert from 0->2 to -1->+1 (clipspace)
  vec2 clipSpace = zeroToTwo - 1.0;

  gl_Position = vec4(clipSpace * vec2(1, -1), 0, 1);

หากคุณดูที่แต่ละขั้นตอนเหล่านั้น ขั้นตอนแรก "แปลงจากพิกเซลเป็น 0.0 เป็น 1.0" คือการดำเนินการเกี่ยวกับการปรับขนาด ประเภทที่ 2 คือการดำเนินการปรับขนาด รายการถัดไปเป็นการแปล และคำสุดท้ายจะมีอัตราส่วน Y เป็น -1 เราสามารถทำทั้งหมดนี้ได้ในเมทริกซ์ที่เราผ่านเข้าไปในตัวปรับแสง เราอาจสร้างเมทริกซ์ 2 มาตรา หนึ่งเมทริกซ์เป็นมาตราส่วน 1.0/ความละเอียด ส่วนอีกค่าหนึ่งมาตราส่วนเป็น 2.0 มาตราที่ 3 แปลด้วย -1.0, -1.0 และมาตราที่ 4 เพื่อมาตราส่วน Y ด้วย -1 แล้วนำค่าเหล่านี้มาคูณกันทั้งหมด แต่เนื่องจากการคำนวณอย่างง่าย เราจะสร้างฟังก์ชันที่ใช้สร้างเมทริกซ์ความละเอียด 'การฉายภาพ' ที่ระบุโดยตรงแทน

function make2DProjection(width, height) {
  // Note: This matrix flips the Y axis so that 0 is at the top.
  return [
    2 / width, 0, 0,
    0, -2 / height, 0,
    -1, 1, 1
  ];
}

ตอนนี้เราสามารถลดความซับซ้อนของตัวปรับแสงเงาได้มากขึ้นไปอีก นี่คือตัวปรับเฉดสี Vertex ใหม่ล่าสุดทั้งหมด

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform mat3 u_matrix;

void main() {
  // Multiply the position by the matrix.
  gl_Position = vec4((u_matrix * vec3(a_position, 1)).xy, 0, 1);
}
</script>

และใน JavaScript เราต้องคูณด้วยเมทริกซ์การฉายภาพ

  // Draw the scene.
  function drawScene() {
    ...
    // Compute the matrices
    var projectionMatrix =
       make2DProjection(canvas.width, canvas.height);
    ...

    // Multiply the matrices.
    var matrix = matrixMultiply(scaleMatrix, rotationMatrix);
    matrix = matrixMultiply(matrix, translationMatrix);
    matrix = matrixMultiply(matrix, projectionMatrix);
    ...
  }

และเรายังนำโค้ดที่กำหนดความละเอียดออกด้วย ในขั้นตอนสุดท้ายนี้ เราได้เปลี่ยนจากตัวให้เฉดสีที่ค่อนข้างซับซ้อนซึ่งมี 6-7 ขั้นตอนสู่การให้เฉดสีแบบง่ายๆ โดยมีขั้นตอนเพียงขั้นตอนเดียวเพื่อให้เกิดความมหัศจรรย์แห่งคณิตศาสตร์แบบเมทริกซ์

เราหวังว่าบทความนี้จะช่วยให้คุณคลายข้อสงสัยเกี่ยวกับคณิตศาสตร์เมทริกซ์ได้ ต่อไปเป็นเรื่อง 3 มิติ ในคณิตศาสตร์เมทริกซ์ 3 มิติจะใช้หลักการและการใช้งานเหมือนกัน ฉันเริ่มด้วยแบบ 2 มิติโดยหวังว่าจะทำให้เข้าใจได้ง่าย