WebGL 2D 変換
3D に進む前に、もう少し 2D について説明します。しばらくお待ちください。この記事は、一部の人にとっては当たり前のことのように思えるかもしれませんが、今後の記事で詳しく説明します。
この記事は、WebGL の基礎から始まるシリーズの続きです。まだ読んでいない場合は、少なくとも最初のチャプターを読んでから、このページに戻ることをおすすめします。変換は、何かを「移動する」ことを意味する、数学的な専門用語です。英語から日本語に文章を移動するのも同じですが、この場合はジオメトリの移動について説明しています。最初の投稿で作成したサンプルコードを使用すると、setRectangle に渡される値を変更するだけで、長方形を簡単に移動できます。前のサンプルに基づくサンプルを以下に示します。
// First lets make some variables
// to hold the translation of the rectangle
var translation = [0, 0];
// then let's make a function to
// re-draw everything. We can call this
// function after we update the translation.
// Draw the scene.
function drawScene() {
// Clear the canvas.
gl.clear(gl.COLOR_BUFFER_BIT);
// Setup a rectangle
setRectangle(gl, translation[0], translation[1], width, height);
// Draw the rectangle.
gl.drawArrays(gl.TRIANGLES, 0, 6);
}
ここまでは順調です。では、より複雑な形状で同じことをしたいとします。次のような 6 つの三角形で構成される「F」を描画するとします。

現在のコードは次のとおりです。setRectangle を次のように変更する必要があります。
// Fill the buffer with the values that define a letter 'F'.
function setGeometry(gl, x, y) {
var width = 100;
var height = 150;
var thickness = 30;
gl.bufferData(
gl.ARRAY_BUFFER,
new Float32Array([
// left column
x, y,
x + thickness, y,
x, y + height,
x, y + height,
x + thickness, y,
x + thickness, y + height,
// top rung
x + thickness, y,
x + width, y,
x + thickness, y + thickness,
x + thickness, y + thickness,
x + width, y,
x + width, y + thickness,
// middle rung
x + thickness, y + thickness * 2,
x + width * 2 / 3, y + thickness * 2,
x + thickness, y + thickness * 3,
x + thickness, y + thickness * 3,
x + width * 2 / 3, y + thickness * 2,
x + width * 2 / 3, y + thickness * 3]),
gl.STATIC_DRAW);
}
スケールしにくいことは明らかです。何百、何千もの線で非常に複雑なジオメトリを描画するには、かなり複雑なコードを記述する必要があります。さらに、描画するたびに JavaScript がすべての点を更新する必要があります。もっと簡単な方法があります。ジオメトリをアップロードし、シェーダーで変換を行うだけです。新しいシェーダーは次のとおりです。
<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;
uniform vec2 u_resolution;
uniform vec2 u_translation;
void main() {
// Add in the translation.
vec2 position = a_position + u_translation;
// convert the rectangle from pixels to 0.0 to 1.0
vec2 zeroToOne = position / u_resolution;
...
コードを少し再構成します。たとえば、ジオメトリを設定するのは 1 回だけです。
// Fill the buffer with the values that define a letter 'F'.
function setGeometry(gl) {
gl.bufferData(
gl.ARRAY_BUFFER,
new Float32Array([
// left column
0, 0,
30, 0,
0, 150,
0, 150,
30, 0,
30, 150,
// top rung
30, 0,
100, 0,
30, 30,
30, 30,
100, 0,
100, 30,
// middle rung
30, 60,
67, 60,
30, 90,
30, 90,
67, 60,
67, 90]),
gl.STATIC_DRAW);
}
次に、目的の移動で描画する前に u_translation を更新します。
...
var translationLocation = gl.getUniformLocation(
program, "u_translation");
...
// Set Geometry.
setGeometry(gl);
..
// Draw scene.
function drawScene() {
// Clear the canvas.
gl.clear(gl.COLOR_BUFFER_BIT);
// Set the translation.
gl.uniform2fv(translationLocation, translation);
// Draw the rectangle.
gl.drawArrays(gl.TRIANGLES, 0, 18);
}
setGeometry は 1 回だけ呼び出されます。drawScene 内にありません。
描画時に、WebGL がほぼすべてを処理します。やっていることは、変換を設定して描画するよう指示することだけです。ジオメトリに数万個のポイントがあっても、メインコードは同じままです。
WebGL 2D 回転
最初に断っておきますが、この説明が理にかなっているかどうかはわかりませんが、試してみる価値はあると思います。
まず、「単位円」について説明します。中学時代の数学を思い出してください(眠くなっちゃだめですよ!)。円には半径があります。円の半径は、円の中心から端までの距離です。単位円は、半径が 1.0 の円です。
3 年生の算数の基本で、何かに 1 を掛けると値は変わらないことを覚えていますか?したがって、123 * 1 = 123 となります。簡単ですね。単位円(半径が 1.0 の円)も 1 の形です。1 が回転しています。つまり、この単位円に何かを掛けることができます。ある意味、1 を掛けるのと似ていますが、魔法が起こり、回転します。単位円上の任意の点から X 値と Y 値を取得し、前のサンプルのジオメトリに掛けます。シェーダーの更新内容は次のとおりです。
<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;
uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;
void main() {
// Rotate the position
vec2 rotatedPosition = vec2(
a_position.x * u_rotation.y + a_position.y * u_rotation.x,
a_position.y * u_rotation.y - a_position.x * u_rotation.x);
// Add in the translation.
vec2 position = rotatedPosition + u_translation;
これらの 2 つの値を渡せるように JavaScript を更新します。
...
var rotationLocation = gl.getUniformLocation(program, "u_rotation");
...
var rotation = [0, 1];
..
// Draw the scene.
function drawScene() {
// Clear the canvas.
gl.clear(gl.COLOR_BUFFER_BIT);
// Set the translation.
gl.uniform2fv(translationLocation, translation);
// Set the rotation.
gl.uniform2fv(rotationLocation, rotation);
// Draw the rectangle.
gl.drawArrays(gl.TRIANGLES, 0, 18);
}
効果的である理由計算式を見てみましょう。
rotatedX = a_position.x * u_rotation.y + a_position.y * u_rotation.x;
rotatedY = a_position.y * u_rotation.y - a_position.x * u_rotation.x;
長方形を回転するとします。回転を開始する前は、右上の角が 3.0、9.0 になっています。単位円上で、12 時から時計回りに 30 度離れた点を選びます。
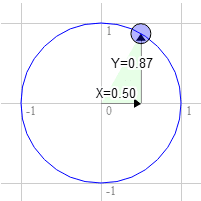
円上の位置は 0.50 と 0.87 です。
3.0 * 0.87 + 9.0 * 0.50 = 7.1
9.0 * 0.87 - 3.0 * 0.50 = 6.3
まさにその場所に

時計回りに 60 度の場合も同様です。
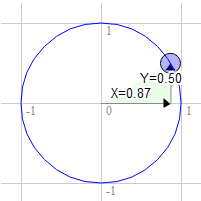
円上の位置は 0.87 と 0.50 です。
3.0 * 0.50 + 9.0 * 0.87 = 9.3
9.0 * 0.50 - 3.0 * 0.87 = 1.9
この点を右回りに回転させると、X 値は大きくなり、Y 値は小さくなることがわかります。90 度を超えると、X は再び小さくなり、Y は大きくなります。このパターンにより、回転が実現されます。単位円上の点には別の名前があります。これらは正弦と余弦と呼ばれます。任意の角度に対して、このようにサインとコサインを調べることができます。
function printSineAndCosineForAnAngle(angleInDegrees) {
var angleInRadians = angleInDegrees * Math.PI / 180;
var s = Math.sin(angleInRadians);
var c = Math.cos(angleInRadians);
console.log("s = " + s + " c = " + c);
}
このコードを JavaScript コンソールにコピーして貼り付け、printSineAndCosignForAngle(30) と入力すると、s = 0.49 c= 0.87 と出力されます(注: 数値は四捨五入しています)。これらをすべて組み合わせることで、ジオメトリを任意の角度に回転させることができます。回転する角度の正弦と余弦に回転を設定します。
...
var angleInRadians = angleInDegrees * Math.PI / 180;
rotation[0] = Math.sin(angleInRadians);
rotation[1] = Math.cos(angleInRadians);
ご理解いただければ幸いです。次に、よりシンプルな方法をご紹介します。スケール。
ラジアンとは
ラジアンとは、円、回転、角度に使用される測定単位です。距離をインチ、ヤード、メートルなどで測定するのと同じように、角度を度数またはラジアンで測定できます。
メートル法で計算するほうが、インチ法で計算するよりも簡単であることはご存じでしょう。インチをフィートにするには、12 で割ります。インチをヤードに変換するには、36 で割ります。36 で割るのは頭の中では難しいですね。指標を使用すると、はるかに簡単です。ミリメートルをセンチメートルに変換するには、10 で割ります。ミリメートルをメートルに変換するには、1,000 で割ります。頭の中で 1,000 で割ることができます。
ラジアン数と度数は類似しています。度単位では計算が難しくなります。ラジアン単位では計算が簡単です。円は 360 度ですが、ラジアンでは 2π 度です。したがって、1 回転は 2π ラジアンです。半回転は π ラジアンです。1/4 回転(90 度)は π/2 ラジアンです。たとえば、何かを 90 度回転させる場合は、Math.PI * 0.5 を使用します。45 度回転させる場合は Math.PI * 0.25 などを使用します。
角度、円、回転に関するほとんどの計算は、ラジアン単位で考えれば非常に簡単に行えます。ぜひお試しください。UI ディスプレイを除き、度ではなくラジアンを使用します。
WebGL 2D スケール
スケーリングは翻訳と同じくらい簡単です。
位置に目的のスケールを掛けます。前の例からの変更点は次のとおりです。
<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;
uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;
uniform vec2 u_scale;
void main() {
// Scale the positon
vec2 scaledPosition = a_position * u_scale;
// Rotate the position
vec2 rotatedPosition = vec2(
scaledPosition.x * u_rotation.y +
scaledPosition.y * u_rotation.x,
scaledPosition.y * u_rotation.y -
scaledPosition.x * u_rotation.x);
// Add in the translation.
vec2 position = rotatedPosition + u_translation;
描画時にスケールを設定するために必要な JavaScript を追加します。
...
var scaleLocation = gl.getUniformLocation(program, "u_scale");
...
var scale = [1, 1];
...
// Draw the scene.
function drawScene() {
// Clear the canvas.
gl.clear(gl.COLOR_BUFFER_BIT);
// Set the translation.
gl.uniform2fv(translationLocation, translation);
// Set the rotation.
gl.uniform2fv(rotationLocation, rotation);
// Set the scale.
gl.uniform2fv(scaleLocation, scale);
// Draw the rectangle.
gl.drawArrays(gl.TRIANGLES, 0, 18);
}
負の値でスケーリングすると、ジオメトリが反転することに注意してください。ここまでの 3 つの章が、移動、回転、スケーリングの理解に役立つことを願っています。次に、これら 3 つを組み合わせて、よりシンプルで有用な形式に変換するマトリックスについて説明します。
「F」はなぜですか?
初めて「F」が使用されているのを見たのは、テクスチャでした。「F」自体は重要ではありません。重要なのは、どの方向からでも向きがわかること。たとえば、ハート ♥ や三角形 △ を使用した場合、横向きに反転されているかどうかを判断できません。円 ○ はさらに悪いです。角ごとに異なる色の四角形を使用するとわかりやすいかもしれませんが、どの角がどの色か覚えておく必要があります。F の向きはすぐに認識できます。

向きを判断できる形状であれば何でも使用できます。私は「F」というアイデアを初めて聞いたときからずっと「F」を使っています。
WebGL 2D 行列
これまでの 3 章では、ジオメトリの移動、ジオメトリの回転、ジオメトリのスケーリングの方法について説明しました。移動、回転、スケーリングはそれぞれ「変換」の一種と見なされます。これらの変換のそれぞれでシェーダーの変更が必要であり、3 つの変換は順序に依存していました。
たとえば、スケールは 2、1、回転は 30%、移動は 100、0 です。

変換は 100,0、回転は 30%、スケーリングは 2, 1 です。

結果はまったく異なります。さらに悪いことに、2 番目の例が必要な場合は、変換、回転、スケールを新しい順序で適用する別のシェーダーを記述する必要があります。私よりはるかに賢い人たちによって、行列演算でも同じことができることがわかりました。2 次元の場合は 3x3 行列を使用します。3x3 マトリックスは、9 つのボックスがあるグリッドのようなものです。
| 1.0 | 2.0 | 3.0 |
| 4.0 | 5.0 | 6.0 |
| 7.0 | 8.0 | 9.0 |
計算を行うには、行列の列に位置を乗算し、結果を合計します。位置には x と y の 2 つの値しかありませんが、この計算を行うには 3 つの値が必要であるため、3 番目の値には 1 を使用します。この場合、結果は次のようになります。
newX = x * 1.0 + y * 4.0 + 1 * 7.0
newY = x * 2.0 + y * 5.0 + 1 * 8.0
extra = x * 3.0 + y * 6.0 + 1 * 9.0
これをご覧になって、「何の意味があるの?」と思われたかもしれません。翻訳があるとします。移動する量を tx と ty とします。次のような行列を作成しましょう。
| 1.0 | 0.0 | 0.0 |
| 0.0 | 1.0 | 0.0 |
| tx | ty | 1.0 |
では、
newX = x * 1.0 + y * 0.0 + 1 * tx
newY = x * 0.0 + y * 1.0 + 1 * ty
extra = x * 0.0 + y * 0.0 + 1 * 1
代数を覚えている方なら、ゼロで乗算する部分はすべて削除できます。1 を掛けても何も変わらないので、式を簡素化して何が起こっているのか確認しましょう。
newX = x + tx;
newY = y + ty;
余分なものは気にしません。これは、翻訳の例の翻訳コードに驚くほど似ています。同様に、回転も行います。回転に関する投稿で説明したように、回転する角度の正弦と余弦のみが必要です。
s = Math.sin(angleToRotateInRadians);
c = Math.cos(angleToRotateInRadians);
次のようなマトリックスを作成します。
| c | -s | 0.0 |
| s | c | 0.0 |
| 0.0 | 0.0 | 1.0 |
行列を適用すると、次のようになります。
newX = x * c + y * s + 1 * 0
newY = x * -s + y * c + 1 * 0
extra = x * 0.0 + y * 0.0 + 1 * 1
0 と 1 で乗算された部分をすべて黒く塗りつぶすと、次のようになります。
newX = x * c + y * s;
newY = x * -s + y * c;
これは、ローテーション サンプルで確認した内容とまったく同じです。最後にスケールです。2 つのスケーリング ファクタを sx と sy とし、次のような行列を作成します。
| sx | 0.0 | 0.0 |
| 0.0 | sy | 0.0 |
| 0.0 | 0.0 | 1.0 |
行列を適用すると、次のようになります。
newX = x * sx + y * 0 + 1 * 0
newY = x * 0 + y * sy + 1 * 0
extra = x * 0.0 + y * 0.0 + 1 * 1
非常に
newX = x * sx;
newY = y * sy;
これは、スケーリング サンプルと同じです。まだ疑問が残っているかもしれません。まとめどういうことだ?これまでと同じことをするために、これほど多くの作業が必要になるのは、大変な作業のように思えます。これが魔法の部分です。行列を乗算して、すべての変換を一度に適用できることがわかりました。2 つの行列を受け取って乗算し、結果を返す関数 matrixMultiply があるとします。わかりやすくするために、平行移動、回転、スケーリングのマトリックスを作成する関数を作成しましょう。
function makeTranslation(tx, ty) {
return [
1, 0, 0,
0, 1, 0,
tx, ty, 1
];
}
function makeRotation(angleInRadians) {
var c = Math.cos(angleInRadians);
var s = Math.sin(angleInRadians);
return [
c,-s, 0,
s, c, 0,
0, 0, 1
];
}
function makeScale(sx, sy) {
return [
sx, 0, 0,
0, sy, 0,
0, 0, 1
];
}
シェーダーを変更しましょう。古いシェーダーは次のようになります。
<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;
uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;
uniform vec2 u_scale;
void main() {
// Scale the positon
vec2 scaledPosition = a_position * u_scale;
// Rotate the position
vec2 rotatedPosition = vec2(
scaledPosition.x * u_rotation.y + scaledPosition.y * u_rotation.x,
scaledPosition.y * u_rotation.y - scaledPosition.x * u_rotation.x);
// Add in the translation.
vec2 position = rotatedPosition + u_translation;
...
新しいシェーダーは、はるかにシンプルになります。
<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;
uniform vec2 u_resolution;
uniform mat3 u_matrix;
void main() {
// Multiply the position by the matrix.
vec2 position = (u_matrix * vec3(a_position, 1)).xy;
...
使用方法
// Draw the scene.
function drawScene() {
// Clear the canvas.
gl.clear(gl.COLOR_BUFFER_BIT);
// Compute the matrices
var translationMatrix =
makeTranslation(translation[0], translation[1]);
var rotationMatrix = makeRotation(angleInRadians);
var scaleMatrix = makeScale(scale[0], scale[1]);
// Multiply the matrices.
var matrix = matrixMultiply(scaleMatrix, rotationMatrix);
matrix = matrixMultiply(matrix, translationMatrix);
// Set the matrix.
gl.uniformMatrix3fv(matrixLocation, false, matrix);
// Draw the rectangle.
gl.drawArrays(gl.TRIANGLES, 0, 18);
}
それでも、何の意味があるのかと疑問に思うかもしれません。あまりメリットがないように思えます。ただし、順序を変更する場合は、新しいシェーダーを記述する必要はありません。計算を変更するだけです。
...
// Multiply the matrices.
var matrix = matrixMultiply(translationMatrix, rotationMatrix);
matrix = matrixMultiply(matrix, scaleMatrix);
...
このような行列を適用できることは、身体の腕、太陽の周りの惑星の月、木の枝などの階層アニメーションにとって特に重要です。階層アニメーションの簡単な例として、「F」を 5 回描画します。ただし、各回、前の「F」のマトリックスから始めます。
// Draw the scene.
function drawScene() {
// Clear the canvas.
gl.clear(gl.COLOR_BUFFER_BIT);
// Compute the matrices
var translationMatrix = makeTranslation(translation[0], translation[1]);
var rotationMatrix = makeRotation(angleInRadians);
var scaleMatrix = makeScale(scale[0], scale[1]);
// Starting Matrix.
var matrix = makeIdentity();
for (var i = 0; i < 5; ++i) {
// Multiply the matrices.
matrix = matrixMultiply(matrix, scaleMatrix);
matrix = matrixMultiply(matrix, rotationMatrix);
matrix = matrixMultiply(matrix, translationMatrix);
// Set the matrix.
gl.uniformMatrix3fv(matrixLocation, false, matrix);
// Draw the geometry.
gl.drawArrays(gl.TRIANGLES, 0, 18);
}
}
これを行うには、単位行列を作成する関数 makeIdentity を導入しました。単位行列は 1.0 を効果的に表す行列であるため、単位行列で乗算しても何も起こりません。
X * 1 = X
so too
matrixX * identity = matrixX
単位行列を作成するコードは次のとおりです。
function makeIdentity() {
return [
1, 0, 0,
0, 1, 0,
0, 0, 1
];
}
もう 1 つの例として、これまでのサンプルでは、左上隅を中心に「F」が回転しています。これは、使用している数学が常に原点を中心に回転し、F の左上隅が原点(0, 0)にあるためです。しかし、今は行列演算を行え、変換の適用順序を選択できるため、残りの変換を適用する前に原点を移動できます。
// make a matrix that will move the origin of the 'F' to
// its center.
var moveOriginMatrix = makeTranslation(-50, -75);
...
// Multiply the matrices.
var matrix = matrixMultiply(moveOriginMatrix, scaleMatrix);
matrix = matrixMultiply(matrix, rotationMatrix);
matrix = matrixMultiply(matrix, translationMatrix);
この方法を使用すると、任意の点から回転またはスケーリングできます。これで、Photoshop または Flash で回転ポイントを移動する方法がわかりました。 もっと複雑な例を挙げてみましょう。WebGL の基礎の最初の記事に戻ると、シェーダーにはピクセルからクリップスペースへの変換コードが次のように記述されていることを思い出すでしょう。
...
// convert the rectangle from pixels to 0.0 to 1.0
vec2 zeroToOne = position / u_resolution;
// convert from 0->1 to 0->2
vec2 zeroToTwo = zeroToOne * 2.0;
// convert from 0->2 to -1->+1 (clipspace)
vec2 clipSpace = zeroToTwo - 1.0;
gl_Position = vec4(clipSpace * vec2(1, -1), 0, 1);
これらのステップを順に見ると、最初のステップ「ピクセルから 0.0 ~ 1.0 に変換」は、実際にはスケール オペレーションです。2 つ目もスケール オペレーションです。2 つ目は移動、3 つ目は Y を -1 倍にスケーリングします。実際には、シェーダーに渡すマトリックスですべて行うことができます。2 つのスケール マトリックス(1 つは 1.0/解像度でスケーリング、もう 1 つは 2.0 でスケーリング、3 つ目は -1.0、-1.0 で移動、4 つ目は Y を -1 でスケーリング)を作成して、それらをすべて掛け算することもできますが、計算が簡単なため、特定の解像度に直接「投影」マトリックスを作成する関数を作成します。
function make2DProjection(width, height) {
// Note: This matrix flips the Y axis so that 0 is at the top.
return [
2 / width, 0, 0,
0, -2 / height, 0,
-1, 1, 1
];
}
これでシェーダーをさらに簡素化できます。新しい頂点シェーダー全体は次のとおりです。
<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;
uniform mat3 u_matrix;
void main() {
// Multiply the position by the matrix.
gl_Position = vec4((u_matrix * vec3(a_position, 1)).xy, 0, 1);
}
</script>
JavaScript では、投影行列を掛ける必要があります。
// Draw the scene.
function drawScene() {
...
// Compute the matrices
var projectionMatrix =
make2DProjection(canvas.width, canvas.height);
...
// Multiply the matrices.
var matrix = matrixMultiply(scaleMatrix, rotationMatrix);
matrix = matrixMultiply(matrix, translationMatrix);
matrix = matrixMultiply(matrix, projectionMatrix);
...
}
また、解像度を設定するコードも削除しました。この最後のステップで、6 ~ 7 ステップの複雑なシェーダーから、行列演算の魔法によって 1 ステップのみの非常にシンプルなシェーダーに移行しました。
この記事が、行列演算の理解に役立てば幸いです。次に 3D に移ります。3D マトリックス数学では、同じ原則と使用方法が適用されます。わかりやすくするために、最初は 2D から始めました。

