इस पेज का अनुवाद Cloud Translation API से किया गया है.

WebGL बदलावों को बेहतर बनाता है

Gregg Tavares

WebGL 2D ट्रांसलेशन

3D पर जाने से पहले, थोड़ी देर के लिए 2D पर ही बने रहें. कृपया थोड़ा इंतज़ार करें. कुछ लोगों को यह लेख बहुत आसान लग सकता है. हालांकि, मैं कुछ लेखों में इस बारे में ज़्यादा जानकारी दूंगा.

यह लेख, WebGL की बुनियादी बातों से शुरू हुई सीरीज़ का अगला लेख है. अगर आपने इसे नहीं पढ़ा है, तो हमारा सुझाव है कि आप कम से कम पहला चैप्टर पढ़ें. इसके बाद, यहां वापस आएं. ट्रांसलेशन, गणित का एक ऐसा नाम है जिसका मतलब है "किसी चीज़ को एक जगह से दूसरी जगह ले जाना". मुझे लगता है कि किसी वाक्य को अंग्रेज़ी से जैपनीज़ में बदलना भी इस कैटगरी में आता है. हालांकि, इस मामले में हम ज्यामिति के बारे में बात कर रहे हैं. पहली पोस्ट में दिए गए सैंपल कोड का इस्तेमाल करके, हमारे रेक्टैंगल को आसानी से ट्रांसलेट किया जा सकता है. इसके लिए, आपको सिर्फ़ setRectangle फ़ंक्शन में दी गई वैल्यू बदलनी होंगी, क्या यह सही है? यहां पिछले सैंपल के आधार पर एक सैंपल दिया गया है.

  // First lets make some variables 
  // to hold the translation of the rectangle
  var translation = [0, 0];
  // then let's make a function to
  // re-draw everything. We can call this
  // function after we update the translation.
  // Draw the scene.
  function drawScene() {
     // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);
    // Setup a rectangle
    setRectangle(gl, translation[0], translation[1], width, height);

    // Draw the rectangle.
    gl.drawArrays(gl.TRIANGLES, 0, 6);
  }

अब तक सब ठीक है. अब कल्पना करें कि हमें एक ज़्यादा मुश्किल आकार के साथ भी यही काम करना है. मान लें कि हमें इस तरह का 'F' बनाना है जिसमें छह त्रिभुज हों.

यहां मौजूदा कोड दिया गया है. हमें setRectangle को कुछ इस तरह बदलना होगा.

// Fill the buffer with the values that define a letter 'F'.
function setGeometry(gl, x, y) {
  var width = 100;
  var height = 150;
  var thickness = 30;
  gl.bufferData(
      gl.ARRAY_BUFFER,
      new Float32Array([
          // left column
          x, y,
          x + thickness, y,
          x, y + height,
          x, y + height,
          x + thickness, y,
          x + thickness, y + height,

          // top rung
          x + thickness, y,
          x + width, y,
          x + thickness, y + thickness,
          x + thickness, y + thickness,
          x + width, y,
          x + width, y + thickness,

          // middle rung
          x + thickness, y + thickness * 2,
          x + width * 2 / 3, y + thickness * 2,
          x + thickness, y + thickness * 3,
          x + thickness, y + thickness * 3,
          x + width * 2 / 3, y + thickness * 2,
          x + width * 2 / 3, y + thickness * 3]),
      gl.STATIC_DRAW);
}

उम्मीद है कि आपको पता चल गया होगा कि यह तरीका बड़े पैमाने पर काम नहीं करेगा. अगर हमें सैकड़ों या हज़ारों लाइनों वाली कोई बहुत जटिल ज्यामिति बनानी है, तो हमें कुछ बहुत जटिल कोड लिखने होंगे. इसके अलावा, हर बार जब हम JavaScript ड्रॉ करते हैं, तो उसे सभी पॉइंट अपडेट करने होते हैं. इसके लिए, एक आसान तरीका है. बस ज्यामिति अपलोड करें और शेडर में ट्रांसलेशन करें. नया शेडर

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform vec2 u_translation;

void main() {
   // Add in the translation.
   vec2 position = a_position + u_translation;

   // convert the rectangle from pixels to 0.0 to 1.0
   vec2 zeroToOne = position / u_resolution;
   ...

और हम कोड को थोड़ा बदल देंगे. एक के लिए, हमें ज्यामिति सिर्फ़ एक बार सेट करनी होगी.

// Fill the buffer with the values that define a letter 'F'.
function setGeometry(gl) {
  gl.bufferData(
      gl.ARRAY_BUFFER,
      new Float32Array([
          // left column
          0, 0,
          30, 0,
          0, 150,
          0, 150,
          30, 0,
          30, 150,

          // top rung
          30, 0,
          100, 0,
          30, 30,
          30, 30,
          100, 0,
          100, 30,

          // middle rung
          30, 60,
          67, 60,
          30, 90,
          30, 90,
          67, 60,
          67, 90]),
      gl.STATIC_DRAW);
}

इसके बाद, हमें अपनी पसंद के अनुवाद के साथ ड्रॉ करने से पहले, सिर्फ़ u_translation को अपडेट करना होगा.

  ...
  var translationLocation = gl.getUniformLocation(
             program, "u_translation");
  ...
  // Set Geometry.
  setGeometry(gl);
  ..
  // Draw scene.
  function drawScene() {
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Set the translation.
    gl.uniform2fv(translationLocation, translation);

    // Draw the rectangle.
    gl.drawArrays(gl.TRIANGLES, 0, 18);
  }

सूचना setGeometry को सिर्फ़ एक बार कॉल किया जाता है. यह अब drawScene में नहीं है.

अब जब हम ड्रॉ करते हैं, तो WebGL असल में सब कुछ कर रहा होता है. हम सिर्फ़ अनुवाद सेट कर रहे हैं और उसे ड्रॉ करने के लिए कह रहे हैं. भले ही, हमारी ज्यामिति में दसियों हज़ार पॉइंट हों, मुख्य कोड पहले जैसा ही रहेगा.

WebGL 2D रोटेशन

मैं शुरू से ही यह स्वीकार करूंगा कि मुझे नहीं पता कि इस बारे में बताने का मेरा तरीका सही होगा या नहीं. हालांकि, कोशिश तो की जा सकती है.

सबसे पहले, आपको "यूनिट सर्कल" के बारे में बताना है. अगर आपको जूनियर हाई स्कूल में पढ़ाया गया गणित याद है (सोने मत जाओ!) तो आपको पता होगा कि सर्कल में त्रिज्या होती है. किसी वृत्त की त्रिज्या, उसके केंद्र से किनारे तक की दूरी होती है. यूनिट सर्कल का मतलब है, त्रिज्या 1.0 वाला वृत्त.

अगर आपको तीसरे ग्रेड के बेसिक मैथ से याद है, तो किसी संख्या को 1 से गुणा करने पर वह संख्या नहीं बदलती. इसलिए, 123 * 1 = 123. काफ़ी आसान है, है ना? यूनिट सर्कल, यानी 1.0 त्रिज्या वाला सर्कल भी 1 का एक फ़ॉर्म है. यह एक घूमता हुआ 1 है. इसलिए, किसी संख्या को इस यूनिट सर्कल से गुणा किया जा सकता है. यह एक तरह से, 1 से गुणा करने जैसा ही है. हालांकि, इसमें जादू होता है और चीज़ें घूमती हैं. हम यूनिट सर्कल के किसी भी पॉइंट से X और Y वैल्यू लेंगे और पिछले सैंपल से अपनी ज्यामिति को उनसे गुणा करेंगे. यहां हमारे शेडर से जुड़े अपडेट दिए गए हैं.

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;

void main() {
  // Rotate the position
  vec2 rotatedPosition = vec2(
     a_position.x * u_rotation.y + a_position.y * u_rotation.x,
     a_position.y * u_rotation.y - a_position.x * u_rotation.x);

  // Add in the translation.
  vec2 position = rotatedPosition + u_translation;

हम JavaScript को अपडेट करते हैं, ताकि हम उन दो वैल्यू को पास कर सकें.

  ...
  var rotationLocation = gl.getUniformLocation(program, "u_rotation");
  ...
  var rotation = [0, 1];
  ..
  // Draw the scene.
  function drawScene() {
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Set the translation.
    gl.uniform2fv(translationLocation, translation);

    // Set the rotation.
    gl.uniform2fv(rotationLocation, rotation);

    // Draw the rectangle.
    gl.drawArrays(gl.TRIANGLES, 0, 18);
  }

यह क्यों काम करता है? ठीक है, हिसाब देखें.

rotatedX = a_position.x * u_rotation.y + a_position.y * u_rotation.x;
rotatedY = a_position.y * u_rotation.y - a_position.x * u_rotation.x;

मान लें कि आपके पास एक रेक्टैंगल है और आपको उसे घुमाना है. घुमाने से पहले, सबसे ऊपर दाएं कोने में 3.0, 9.0 दिखता है. आइए, यूनिट सर्कल पर 12 बजे से घड़ी की दिशा में 30 डिग्री पर कोई पॉइंट चुनें.

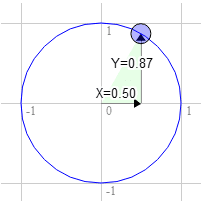
सर्कल पर इनकी पोज़िशन 0.50 और 0.87 है

3.0 * 0.87 + 9.0 * 0.50 = 7.1
9.0 * 0.87 - 3.0 * 0.50 = 6.3

हमें यही चाहिए

घड़ी की दिशा में 60 डिग्री के लिए भी यही तरीका अपनाएं

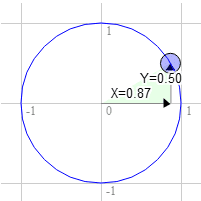
सर्कल पर उसकी पोज़िशन 0.87 और 0.50 है

3.0 * 0.50 + 9.0 * 0.87 = 9.3
9.0 * 0.50 - 3.0 * 0.87 = 1.9

आप देख सकते हैं कि उस पॉइंट को दाईं ओर घुमाने पर, X वैल्यू बड़ी हो जाती है और Y वैल्यू छोटी हो जाती है. अगर 90 डिग्री से ज़्यादा घुमाया जाता है, तो X फिर से छोटा होने लगेगा और Y बड़ा होने लगेगा. इस पैटर्न से हमें रोटेशन मिलता है. यूनिट सर्कल पर मौजूद पॉइंट का एक और नाम है. इन्हें साइन और कोसाइन कहा जाता है. इसलिए, किसी भी कोण के लिए, हम साइन और कोसाइन को इस तरह देख सकते हैं.

function printSineAndCosineForAnAngle(angleInDegrees) {
  var angleInRadians = angleInDegrees * Math.PI / 180;
  var s = Math.sin(angleInRadians);
  var c = Math.cos(angleInRadians);
  console.log("s = " + s + " c = " + c);
}

अगर कोड को कॉपी करके अपने JavaScript कंसोल में चिपकाया जाता है और printSineAndCosignForAngle(30) टाइप किया जाता है, तो आपको s = 0.49 c= 0.87 दिखेगा. ध्यान दें: मैंने संख्याओं को राउंड ऑफ़ किया है. इन सभी को एक साथ जोड़ने पर, अपनी ज्यामिति को अपनी पसंद के हिसाब से किसी भी ऐंगल पर घुमाया जा सकता है. आपको जिस ऐंगल पर घुमाना है उसके साइन और कोसाइन पर रोटेशन सेट करें.

  ...
  var angleInRadians = angleInDegrees * Math.PI / 180;
  rotation[0] = Math.sin(angleInRadians);
  rotation[1] = Math.cos(angleInRadians);

हमें उम्मीद है कि आपको यह समझ आ गया होगा. अगला उदाहरण ज़्यादा आसान है. स्केल.

रेडियन क्या होते हैं?

रेडियन, मेज़रमेंट की एक इकाई है. इसका इस्तेमाल सर्कल, रोटेशन, और ऐंगल के साथ किया जाता है. जिस तरह दूरी को इंच, यार्ड, मीटर वगैरह में मापा जा सकता है उसी तरह कोणों को डिग्री या रेडियन में मापा जा सकता है.

शायद आपको पता हो कि मेट्रिक मापों के साथ गणित करना, इंपीरियल मापों के साथ गणित करने से आसान है. इंच को फ़ीट में बदलने के लिए, उसे 12 से भाग दें. इंच को यार्ड में बदलने के लिए, उसे 36 से भाग दें. मुझे नहीं पता कि आपके बारे में क्या है, लेकिन मैं अपने हिसाब से 36 से भाग नहीं लगा सकता. मेट्रिक की मदद से, यह काम ज़्यादा आसान हो जाता है. मिलीमीटर को सेंटीमीटर में बदलने के लिए, उसे 10 से भाग दें. मिलीमीटर को मीटर में बदलने के लिए, उसे 1,000 से भाग दें. मैं अपने हिसाब से 1000 से भाग कर सकता/सकती हूं.

रेडियन और डिग्री एक जैसे होते हैं. डिग्री की वजह से गणित का हिसाब लगाना मुश्किल हो जाता है. रेडियन की मदद से, गणित आसानी से किया जा सकता है. एक सर्कल में 360 डिग्री होते हैं, लेकिन सिर्फ़ 2π रेडियन होते हैं. इसलिए, एक पूरा चक्कर 2π रेडियन होता है. आधा घुमाव π रेडियन होता है. 1/4 टर्न यानी 90 डिग्री, π/2 रेडियन होता है. इसलिए, अगर आपको किसी आइटम को 90 डिग्री घुमाना है, तो बस Math.PI * 0.5 का इस्तेमाल करें. अगर आपको इसे 45 डिग्री घुमाना है, तो Math.PI * 0.25 वगैरह का इस्तेमाल करें.

रेडियन में सोचने पर, कोण, सर्कल या रोटेशन से जुड़े गणित के लगभग सभी सवाल आसानी से हल हो जाते हैं. इसलिए, इसे आज़माएं. यूज़र इंटरफ़ेस (यूआई) डिसप्ले के अलावा, डिग्री के बजाय रेडियन का इस्तेमाल करें.

WebGL 2D स्केल

अनुवाद करने की तरह ही, स्केलिंग भी आसान है.

हम पोज़िशन को अपने मनमुताबिक स्केल से गुणा करते हैं. यहां हमारे पिछले सैंपल में किए गए बदलावों के बारे में बताया गया है.

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;
uniform vec2 u_scale;

void main() {
  // Scale the positon
  vec2 scaledPosition = a_position * u_scale;

  // Rotate the position
  vec2 rotatedPosition = vec2(
     scaledPosition.x * u_rotation.y +
        scaledPosition.y * u_rotation.x,
     scaledPosition.y * u_rotation.y -
        scaledPosition.x * u_rotation.x);

  // Add in the translation.
  vec2 position = rotatedPosition + u_translation;

और हम ड्रॉ करते समय स्केल सेट करने के लिए ज़रूरी JavaScript जोड़ते हैं.

  ...
  var scaleLocation = gl.getUniformLocation(program, "u_scale");
  ...
  var scale = [1, 1];
  ...
  // Draw the scene.
  function drawScene() {
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Set the translation.
    gl.uniform2fv(translationLocation, translation);

    // Set the rotation.
    gl.uniform2fv(rotationLocation, rotation);

    // Set the scale.
    gl.uniform2fv(scaleLocation, scale);

    // Draw the rectangle.
    gl.drawArrays(gl.TRIANGLES, 0, 18);
  }

ध्यान दें कि नेगेटिव वैल्यू के हिसाब से स्केलिंग करने पर, हमारी ज्यामिति फ़्लिप हो जाती है. हमें उम्मीद है कि पिछले तीन चैप्टर में, ट्रांसलेशन, रोटेशन, और स्केल को समझने में आपको मदद मिली होगी. अगले लेख में, हम मैट्रिक के जादू के बारे में जानेंगे. मैट्रिक, इन तीनों को एक बहुत ही आसान और ज़्यादा काम के फ़ॉर्मैट में जोड़ती है.

'F' ग्रेड क्यों?

मैंने पहली बार किसी को टेक्सचर पर 'F' का इस्तेमाल करते हुए देखा था. 'F' का मतलब ज़रूरी नहीं है. ज़रूरी बात यह है कि किसी भी दिशा से, उसके ओरिएंटेशन का पता लगाया जा सके. उदाहरण के लिए, अगर हमने दिल ♥ या त्रिकोण △ का इस्तेमाल किया है, तो हम यह नहीं बता सकते कि उसे हॉरिज़ॉन्टल तौर पर फ़्लिप किया गया है या नहीं. सर्कल ○ का इस्तेमाल करना और भी खराब होगा. रंगीन रेक्टैंगल, हर कोने पर अलग-अलग रंगों के साथ काम करेगा. हालांकि, आपको यह याद रखना होगा कि कौनसा कोना किस रंग का है. F के ओरिएंटेशन को तुरंत पहचाना जा सकता है.

किसी भी आकार का इस्तेमाल किया जा सकता है. हालांकि, यह ज़रूरी है कि आप उस आकार के ओरिएंटेशन के बारे में बता सकें. मैंने इस आइडिया के बारे में 'पहली' बार जानने के बाद से ही 'F' का इस्तेमाल किया है.

WebGL 2D मैट्रिक्स

पिछले तीन चैप्टर में, हमने ज्यामिति को ट्रांसलेट करने, घुमाने, और स्केल करने का तरीका जाना. ट्रांसलेशन, रोटेशन, और स्केल को 'ट्रांसफ़ॉर्मेशन' माना जाता है. इनमें से हर ट्रांसफ़ॉर्मेशन के लिए, शेडर में बदलाव करना ज़रूरी था. साथ ही, तीनों ट्रांसफ़ॉर्मेशन का क्रम भी ज़रूरी था.

उदाहरण के लिए, यहां स्केल 2, 1, रोटेशन 30%, और ट्रांसलेशन 100, 0 है.

यहां 100,0 का ट्रांसलेशन, 30% का रोटेशन, और 2, 1 का स्केल है

नतीजे पूरी तरह से अलग-अलग होते हैं. इससे भी बुरा यह है कि अगर हमें दूसरा उदाहरण चाहिए, तो हमें एक अलग शेडर लिखना होगा, जो हमारे नए क्रम में ट्रांसलेशन, रोटेशन, और स्केल लागू करता है. खैर, मेरे मुकाबले ज़्यादा स्मार्ट कुछ लोगों ने यह पता लगाया कि मैट्रिक्स मैथ का इस्तेमाल करके भी वही काम किए जा सकते हैं. 2D के लिए, हम 3x3 मैट्रिक का इस्तेमाल करते हैं. 3x3 मैट्रिक्स, 9 बॉक्स वाले ग्रिड की तरह होती है.

1.0	2.0	3.0
4.0	5.0	6.0
7.0	8.0	9.0

गणित करने के लिए, हम मैट्रिक के कॉलम में नीचे की ओर मौजूद पोज़िशन को गुणा करते हैं और नतीजों को जोड़ते हैं. हमारी पोज़िशन में सिर्फ़ दो वैल्यू, x और y हैं. हालांकि, यह हिसाब लगाने के लिए, हमें तीन वैल्यू की ज़रूरत है. इसलिए, हम तीसरी वैल्यू के लिए 1 का इस्तेमाल करेंगे. इस मामले में, हमारा नतीजा

newX = x * 1.0 + y * 4.0 + 1 * 7.0

newY = x * 2.0 + y * 5.0 + 1 * 8.0

extra = x * 3.0 + y * 6.0 + 1 * 9.0

शायद आपको यह देखकर लग रहा हो कि "इसका क्या फ़ायदा है". मान लें कि हमारे पास अनुवाद है. हम उस रकम को tx और ty कहेंगे जिसका अनुवाद करना है. चलिए, इस तरह का मैट्रिक बनाते हैं

1.0	0.0	0.0
0.0	1.0	0.0
tx	ty	1.0

अब इसे देखें

newX = x * 1.0 + y * 0.0 + 1 * tx

newY = x * 0.0 + y * 1.0 + 1 * ty

extra = x * 0.0 + y * 0.0 + 1 * 1

अगर आपको बीजगणित याद है, तो हम शून्य से गुणा होने वाली किसी भी जगह को मिटा सकते हैं. एक से गुणा करने पर कोई असर नहीं पड़ता. इसलिए, यह जानने के लिए कि क्या हो रहा है, इसे आसान बनाएं

newX = x + tx;
newY = y + ty;

और अतिरिक्त जानकारी की हमें ज़्यादा परवाह नहीं है. यह अनुवाद के हमारे उदाहरण में दिए गए अनुवाद कोड जैसा ही दिखता है. इसी तरह, आइए रोटेशन की सुविधा को इस्तेमाल करके देखें. जैसा कि हमने रोटेशन पोस्ट में बताया था, हमें सिर्फ़ उस ऐंगल के साइन और कोसाइन की ज़रूरत होती है जिसे हमें घुमाना है.

s = Math.sin(angleToRotateInRadians);
c = Math.cos(angleToRotateInRadians);

और हम इस तरह का मैट्रिक बनाते हैं

c	-s	0.0
s	c	0.0
0.0	0.0	1.0

मैट्रिक लागू करने पर, हमें यह मिलता है

newX = x * c + y * s + 1 * 0

newY = x * -s + y * c + 1 * 0

extra = x * 0.0 + y * 0.0 + 1 * 1

0 और 1 से गुणा किए गए सभी अंकों को काला कर देने पर, हमें यह वैल्यू मिलती है

newX = x *  c + y * s;
newY = x * -s + y * c;

यह वही है जो हमारे रोटेशन सैंपल में था. आखिर में, स्केल. हम अपने दो स्केल फ़ैक्टर को sx और sy कहेंगे और हम इस तरह का मैट्रिक बनाएंगे

sx	0.0	0.0
0.0	sy	0.0
0.0	0.0	1.0

मैट्रिक लागू करने पर, हमें यह मिलता है

newX = x * sx + y * 0 + 1 * 0

newY = x * 0 + y * sy + 1 * 0

extra = x * 0.0 + y * 0.0 + 1 * 1

जो असल में

newX = x * sx;
newY = y * sy;

यह हमारे स्केलिंग सैंपल जैसा ही है. हमें यकीन है कि आप अब भी सोच रहे होंगे. तो क्या? इसका क्या मतलब है. क्या हमें वही काम करने के लिए इतना ज़्यादा काम करना होगा जो पहले से किया जा रहा है? यहां जादू की बात आती है. इससे पता चलता है कि हम मैट्रिस को एक साथ गुणा कर सकते हैं और सभी बदलाव एक साथ लागू कर सकते हैं. मान लें कि हमारे पास matrixMultiply फ़ंक्शन है, जो दो मैट्रिक लेता है, उनका गुणा करता है, और नतीजा दिखाता है. चीज़ों को साफ़ तौर पर समझने के लिए, ट्रांसलेशन, रोटेशन, और स्केल के लिए मैट्रिक बनाने वाले फ़ंक्शन बनाते हैं.

function makeTranslation(tx, ty) {
  return [
    1, 0, 0,
    0, 1, 0,
    tx, ty, 1
  ];
}

function makeRotation(angleInRadians) {
  var c = Math.cos(angleInRadians);
  var s = Math.sin(angleInRadians);
  return [
    c,-s, 0,
    s, c, 0,
    0, 0, 1
  ];
}

function makeScale(sx, sy) {
  return [
    sx, 0, 0,
    0, sy, 0,
    0, 0, 1
  ];
}

अब चलिए, अपना शेडर बदलते हैं. पुराना शेडर कुछ ऐसा दिखता था

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;
uniform vec2 u_scale;

void main() {
  // Scale the positon
  vec2 scaledPosition = a_position * u_scale;

  // Rotate the position
  vec2 rotatedPosition = vec2(
     scaledPosition.x * u_rotation.y + scaledPosition.y * u_rotation.x,
     scaledPosition.y * u_rotation.y - scaledPosition.x * u_rotation.x);

  // Add in the translation.
  vec2 position = rotatedPosition + u_translation;
  ...

हमारा नया शेडर बहुत आसान होगा.

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform mat3 u_matrix;

void main() {
  // Multiply the position by the matrix.
  vec2 position = (u_matrix * vec3(a_position, 1)).xy;
  ...

हम इसका इस्तेमाल इस तरह करते हैं

  // Draw the scene.
  function drawScene() {
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Compute the matrices
    var translationMatrix =
       makeTranslation(translation[0], translation[1]);
    var rotationMatrix = makeRotation(angleInRadians);
    var scaleMatrix = makeScale(scale[0], scale[1]);

    // Multiply the matrices.
    var matrix = matrixMultiply(scaleMatrix, rotationMatrix);
    matrix = matrixMultiply(matrix, translationMatrix);

    // Set the matrix.
    gl.uniformMatrix3fv(matrixLocation, false, matrix);

    // Draw the rectangle.
    gl.drawArrays(gl.TRIANGLES, 0, 18);
  }

आपके मन में सवाल उठ सकता है कि इससे क्या फ़ायदा? ऐसा लगता है कि इससे ज़्यादा फ़ायदा नहीं मिलेगा . हालांकि, अब अगर हमें क्रम बदलना है, तो हमें नया शेडर लिखने की ज़रूरत नहीं है. हम सिर्फ़ हिसाब-किताब बदल सकते हैं.

    ...
    // Multiply the matrices.
    var matrix = matrixMultiply(translationMatrix, rotationMatrix);
    matrix = matrixMultiply(matrix, scaleMatrix);
    ...

इस तरह की मैट्रिक लागू करना, हैरारकी वाले ऐनिमेशन के लिए खास तौर पर ज़रूरी है. जैसे, किसी शरीर पर हाथ, सूरज के चारों ओर मौजूद चंद्रमा या पेड़ की शाखाएं. हैरारकी वाले ऐनिमेशन का आसान उदाहरण देने के लिए, 'F' को पांच बार ड्रॉ करें. हालांकि, हर बार पिछले 'F' के मैट्रिक से शुरू करें.

  // Draw the scene.
  function drawScene() {
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Compute the matrices
    var translationMatrix = makeTranslation(translation[0], translation[1]);
    var rotationMatrix = makeRotation(angleInRadians);
    var scaleMatrix = makeScale(scale[0], scale[1]);

    // Starting Matrix.
    var matrix = makeIdentity();

    for (var i = 0; i < 5; ++i) {
      // Multiply the matrices.
      matrix = matrixMultiply(matrix, scaleMatrix);
      matrix = matrixMultiply(matrix, rotationMatrix);
      matrix = matrixMultiply(matrix, translationMatrix);

      // Set the matrix.
      gl.uniformMatrix3fv(matrixLocation, false, matrix);

      // Draw the geometry.
      gl.drawArrays(gl.TRIANGLES, 0, 18);
    }
  }

इसके लिए, हमने makeIdentity फ़ंक्शन को पेश किया है, जो आइडेंटिटी मैट्रिक बनाता है. आइडेंटिटी मैट्रिक्स एक ऐसी मैट्रिक्स होती है जो 1.0 को असरदार तरीके से दिखाती है, ताकि आइडेंटिटी से गुणा करने पर कुछ न हो. ठीक वैसे ही जैसे

X * 1 = X

so too

matrixX * identity = matrixX

आइडेंटिटी मैट्रिक बनाने के लिए कोड यहां दिया गया है.

function makeIdentity() {
  return [
    1, 0, 0,
    0, 1, 0,
    0, 0, 1
  ];
}

एक और उदाहरण, अब तक के हर सैंपल में, हमारा 'F' अपने सबसे ऊपर बाईं ओर मौजूद कोने के आस-पास घूमता है. ऐसा इसलिए होता है, क्योंकि हम जिस मैथ का इस्तेमाल कर रहे हैं वह हमेशा ऑरिजिन के आस-पास घूमता रहता है. साथ ही, हमारे 'F' का सबसे ऊपर बायां कोना ऑरिजिन (0, 0) पर होता है अब, मैट्रिक मैथ का इस्तेमाल करने और ट्रांसफ़ॉर्म के लागू होने के क्रम को चुनने की वजह से, हम बाकी ट्रांसफ़ॉर्म लागू होने से पहले ऑरिजिन को मूव कर सकते हैं.

    // make a matrix that will move the origin of the 'F' to
    // its center.
    var moveOriginMatrix = makeTranslation(-50, -75);
    ...

    // Multiply the matrices.
    var matrix = matrixMultiply(moveOriginMatrix, scaleMatrix);
    matrix = matrixMultiply(matrix, rotationMatrix);
    matrix = matrixMultiply(matrix, translationMatrix);

इस तकनीक का इस्तेमाल करके, किसी भी बिंदु से आइटम को घुमाया या स्केल किया जा सकता है. अब आपको पता है कि Photoshop या Flash में, रोटेशन पॉइंट को कैसे घुमाया जा सकता है. आइए, और भी क्रेज़ी चीज़ें करते हैं. WebGL के बुनियादी सिद्धांतों के बारे में पहले लेख पर वापस जाकर, आपको याद होगा कि पिक्सल से क्लिपस्पेस में बदलने के लिए, हमारे पास शेडर में यह कोड है.

  ...
  // convert the rectangle from pixels to 0.0 to 1.0
  vec2 zeroToOne = position / u_resolution;

  // convert from 0->1 to 0->2
  vec2 zeroToTwo = zeroToOne * 2.0;

  // convert from 0->2 to -1->+1 (clipspace)
  vec2 clipSpace = zeroToTwo - 1.0;

  gl_Position = vec4(clipSpace * vec2(1, -1), 0, 1);

इनमें से हर चरण को बारी-बारी से देखें, तो पहला चरण, "पिक्सल से 0.0 से 1.0 में बदलना", असल में स्केल करने की प्रोसेस है. दूसरा भी स्केल ऑपरेशन है. अगला स्टेटमेंट, अनुवाद है और आखिरी स्टेटमेंट में Y को -1 से स्केल किया गया है. हम शेडर में पास किए गए मैट्रिक्स में, यह सब कर सकते हैं. हम दो स्केल मैट्रिक बना सकते हैं. पहला, 1.0/रिज़ॉल्यूशन के हिसाब से स्केल करने के लिए, दूसरा 2.0 के हिसाब से स्केल करने के लिए, तीसरा -1.0,-1.0 के हिसाब से ट्रांसलेट करने के लिए, और चौथा Y को -1 के हिसाब से स्केल करने के लिए. इसके बाद, इन सभी को एक साथ गुणा करें. हालांकि, गणित आसान होने की वजह से, हम सिर्फ़ एक फ़ंक्शन बनाएंगे, जो किसी दिए गए रिज़ॉल्यूशन के लिए सीधे 'प्रोजेक्शन' मैट्रिक बनाता है.

function make2DProjection(width, height) {
  // Note: This matrix flips the Y axis so that 0 is at the top.
  return [
    2 / width, 0, 0,
    0, -2 / height, 0,
    -1, 1, 1
  ];
}

अब हम शेडर को और भी आसान बना सकते हैं. यहां पूरा नया वर्टिक्स शेडर दिया गया है.

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform mat3 u_matrix;

void main() {
  // Multiply the position by the matrix.
  gl_Position = vec4((u_matrix * vec3(a_position, 1)).xy, 0, 1);
}
</script>

और JavaScript में, हमें प्रोजेक्शन मैट्रिक्स से गुणा करना होगा

  // Draw the scene.
  function drawScene() {
    ...
    // Compute the matrices
    var projectionMatrix =
       make2DProjection(canvas.width, canvas.height);
    ...

    // Multiply the matrices.
    var matrix = matrixMultiply(scaleMatrix, rotationMatrix);
    matrix = matrixMultiply(matrix, translationMatrix);
    matrix = matrixMultiply(matrix, projectionMatrix);
    ...
  }

हमने रिज़ॉल्यूशन सेट करने वाला कोड भी हटा दिया है. इस आखिरी चरण में, हम 6-7 चरणों वाले जटिल शेडर से, सिर्फ़ एक चरण वाले बहुत आसान शेडर पर आ गए हैं. ऐसा मैट्रिक मैथ के जादू की वजह से हुआ है.

हमें उम्मीद है कि इस लेख से आपको मैट्रिक्स के गणित को समझने में मदद मिली होगी. इसके बाद, मैं 3D पर जाऊंगा. 3D मैट्रिक में, गणित के वही सिद्धांत और इस्तेमाल लागू होते हैं. मैंने 2D से शुरुआत की, ताकि इसे समझना आसान हो.