Эта страница переведена с помощью Cloud Translation API.

WebGL преобразует

Gregg Tavares

WebGL 2D-перевод

Прежде чем мы перейдем к 3D, давайте еще немного остановимся на 2D. Потерпите меня, пожалуйста. Кому-то эта статья может показаться слишком очевидной, но я остановлюсь на этом в нескольких статьях.

Эта статья является продолжением серии, начинающейся с «Основы WebGL» . Если вы еще не читали, советую вам прочитать хотя бы первую главу, а затем вернуться сюда. Перевод — это какое-то причудливое математическое название, которое по сути означает «перемещать» что-то. Я полагаю, что перенос предложения с английского на японский тоже подойдет, но в данном случае мы говорим о перемещении геометрии. Используя пример кода, который мы получили в первом посте, вы могли бы легко перевести наш прямоугольник, просто изменив значения, передаваемые в setRectangle, верно? Вот образец, основанный на нашем предыдущем образце .

  // First lets make some variables 
  // to hold the translation of the rectangle
  var translation = [0, 0];
  // then let's make a function to
  // re-draw everything. We can call this
  // function after we update the translation.
  // Draw the scene.
  function drawScene() {
     // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);
    // Setup a rectangle
    setRectangle(gl, translation[0], translation[1], width, height);

    // Draw the rectangle.
    gl.drawArrays(gl.TRIANGLES, 0, 6);
  }

Все идет нормально. Но теперь представьте, что мы хотим сделать то же самое с более сложной формой. Допустим, мы хотели нарисовать букву «F», состоящую из шести треугольников.

Итак, ниже приведен текущий код, который нам придется изменить setRectangle на что-то более похожее на этот.

// Fill the buffer with the values that define a letter 'F'.
function setGeometry(gl, x, y) {
  var width = 100;
  var height = 150;
  var thickness = 30;
  gl.bufferData(
      gl.ARRAY_BUFFER,
      new Float32Array([
          // left column
          x, y,
          x + thickness, y,
          x, y + height,
          x, y + height,
          x + thickness, y,
          x + thickness, y + height,

          // top rung
          x + thickness, y,
          x + width, y,
          x + thickness, y + thickness,
          x + thickness, y + thickness,
          x + width, y,
          x + width, y + thickness,

          // middle rung
          x + thickness, y + thickness * 2,
          x + width * 2 / 3, y + thickness * 2,
          x + thickness, y + thickness * 3,
          x + thickness, y + thickness * 3,
          x + width * 2 / 3, y + thickness * 2,
          x + width * 2 / 3, y + thickness * 3]),
      gl.STATIC_DRAW);
}

Надеюсь, вы увидите, что это не будет хорошо масштабироваться. Если мы хотим нарисовать очень сложную геометрию с сотнями или тысячами линий, нам придется написать довольно сложный код. Кроме того, каждый раз, когда мы рисуем, JavaScript должен обновлять все точки. Есть более простой способ. Просто загрузите геометрию и выполните перевод в шейдере. Вот новый шейдер

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform vec2 u_translation;

void main() {
   // Add in the translation.
   vec2 position = a_position + u_translation;

   // convert the rectangle from pixels to 0.0 to 1.0
   vec2 zeroToOne = position / u_resolution;
   ...

и мы немного реструктурируем код. Во-первых, нам нужно установить геометрию только один раз.

// Fill the buffer with the values that define a letter 'F'.
function setGeometry(gl) {
  gl.bufferData(
      gl.ARRAY_BUFFER,
      new Float32Array([
          // left column
          0, 0,
          30, 0,
          0, 150,
          0, 150,
          30, 0,
          30, 150,

          // top rung
          30, 0,
          100, 0,
          30, 30,
          30, 30,
          100, 0,
          100, 30,

          // middle rung
          30, 60,
          67, 60,
          30, 90,
          30, 90,
          67, 60,
          67, 90]),
      gl.STATIC_DRAW);
}

Тогда нам просто нужно обновить u_translation , прежде чем мы нарисуем желаемый перевод.

  ...
  var translationLocation = gl.getUniformLocation(
             program, "u_translation");
  ...
  // Set Geometry.
  setGeometry(gl);
  ..
  // Draw scene.
  function drawScene() {
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Set the translation.
    gl.uniform2fv(translationLocation, translation);

    // Draw the rectangle.
    gl.drawArrays(gl.TRIANGLES, 0, 18);
  }

Обратите внимание, setGeometry вызывается только один раз. Его больше нет внутри drawScene.

Теперь, когда мы рисуем, WebGL делает практически всё. Все, что мы делаем, это устанавливаем перевод и просим его отрисовать. Даже если бы наша геометрия имела десятки тысяч точек, основной код остался бы прежним.

WebGL 2D вращение

Я сразу признаюсь, что понятия не имею, будет ли иметь смысл то, как я это объясню, но какого черта, может, стоит попробовать.

Сначала я хочу познакомить вас с так называемым «единичным кругом». Если вы помните школьную математику (не спите на мне!), у круга есть радиус. Радиус круга – это расстояние от центра круга до края. Единичная окружность — это окружность радиусом 1,0.

Если вы помните из базовой математики 3-го класса, если вы умножите что-то на 1, оно останется прежним. Итак, 123 * 1 = 123. Довольно просто, правда? Ну, единичный круг, круг с радиусом 1,0 также является формой 1. Это вращающаяся 1. Таким образом, вы можете умножить что-то на этот единичный круг, и в каком-то смысле это похоже на умножение на 1, за исключением того, что происходит волшебство и тому подобное. вращать. Мы возьмем значения X и Y из любой точки единичного круга и умножим на них нашу геометрию из нашего предыдущего примера . Вот обновления нашего шейдера.

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;

void main() {
  // Rotate the position
  vec2 rotatedPosition = vec2(
     a_position.x * u_rotation.y + a_position.y * u_rotation.x,
     a_position.y * u_rotation.y - a_position.x * u_rotation.x);

  // Add in the translation.
  vec2 position = rotatedPosition + u_translation;

И мы обновляем JavaScript, чтобы можно было передать эти два значения.

  ...
  var rotationLocation = gl.getUniformLocation(program, "u_rotation");
  ...
  var rotation = [0, 1];
  ..
  // Draw the scene.
  function drawScene() {
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Set the translation.
    gl.uniform2fv(translationLocation, translation);

    // Set the rotation.
    gl.uniform2fv(rotationLocation, rotation);

    // Draw the rectangle.
    gl.drawArrays(gl.TRIANGLES, 0, 18);
  }

Почему это работает? Ну, посмотрите на математику.

rotatedX = a_position.x * u_rotation.y + a_position.y * u_rotation.x;
rotatedY = a_position.y * u_rotation.y - a_position.x * u_rotation.x;

Допустим, у вас есть прямоугольник, и вы хотите его повернуть. Прежде чем вы начнете вращать его, верхний правый угол будет иметь значения 3.0, 9.0. Давайте выберем точку на единичном круге на 30 градусов по часовой стрелке от 12 часов.

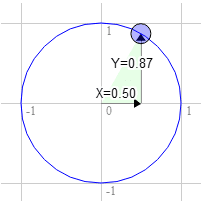
Позиция на круге там 0,50 и 0,87.

3.0 * 0.87 + 9.0 * 0.50 = 7.1
9.0 * 0.87 - 3.0 * 0.50 = 6.3

Это именно то место, где нам нужно, чтобы это было

То же для 60 градусов по часовой стрелке.

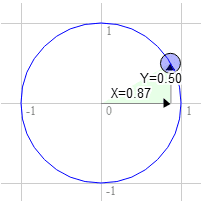
Позиция на круге там 0,87 и 0,50.

3.0 * 0.50 + 9.0 * 0.87 = 9.3
9.0 * 0.50 - 3.0 * 0.87 = 1.9

Вы можете видеть, что когда мы поворачиваем эту точку по часовой стрелке вправо, значение X увеличивается, а значение Y уменьшается. Если продолжать движение за пределы 90 градусов, X снова начнет уменьшаться, а Y начнет увеличиваться. Этот шаблон дает нам вращение. Есть другое название точек единичного круга. Их называют синус и косинус. Итак, для любого заданного угла мы можем просто найти синус и косинус вот так.

function printSineAndCosineForAnAngle(angleInDegrees) {
  var angleInRadians = angleInDegrees * Math.PI / 180;
  var s = Math.sin(angleInRadians);
  var c = Math.cos(angleInRadians);
  console.log("s = " + s + " c = " + c);
}

Если вы скопируете и вставите код в консоль JavaScript и наберете printSineAndCosignForAngle(30) вы увидите, что он печатает s = 0.49 c= 0.87 (примечание: я округлил числа.) Если вы соберете все это вместе, вы сможете повернуть свою геометрию в любое положение. желаемый угол. Просто установите вращение на синус и косинус угла, на который вы хотите повернуть.

  ...
  var angleInRadians = angleInDegrees * Math.PI / 180;
  rotation[0] = Math.sin(angleInRadians);
  rotation[1] = Math.cos(angleInRadians);

Надеюсь, это имело какой-то смысл. Дальше попроще. Шкала.

Что такое радианы?

Радианы — это единица измерения, используемая для измерения окружностей, вращения и углов. Точно так же, как мы можем измерять расстояние в дюймах, ярдах, метрах и т. д., мы можем измерять углы в градусах или радианах.

Вы, вероятно, знаете, что математика с метрическими единицами измерения проще, чем с британскими единицами измерения. Чтобы перейти от дюймов к футам, мы делим на 12. Чтобы перейти от дюймов к ярдам, мы делим на 36. Не знаю, как вы, но я не могу разделить на 36 в уме. С метрикой все гораздо проще. Чтобы перейти от миллиметров к сантиметрам, мы делим на 10. Чтобы перейти от миллиметров к метрам, мы делим на 1000. Я могу разделить на 1000 в уме.

Радианы и градусы аналогичны. Градусы усложняют математику. Радианы упрощают математику. В круге 360 градусов, но всего 2π радиан. Таким образом, полный оборот равен 2π радиан. Пол-оборота — это π радиан. 1/4 оборота, т.е. 90 градусов, составляет π/2 радиана. Итак, если вы хотите повернуть что-то на 90 градусов, просто используйте Math.PI * 0.5 . Если вы хотите повернуть его на 45 градусов, используйте Math.PI * 0.25 и т. д.

Почти вся математика, связанная с углами, окружностями и вращением, работает очень просто, если вы начнете думать в радианах. Так что попробуйте. Используйте радианы, а не градусы, за исключением отображений пользовательского интерфейса.

WebGL 2D-масштаб

Масштабирование так же просто, как и перевод.

Умножаем положение на желаемый масштаб. Вот изменения по сравнению с нашим предыдущим образцом.

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;
uniform vec2 u_scale;

void main() {
  // Scale the positon
  vec2 scaledPosition = a_position * u_scale;

  // Rotate the position
  vec2 rotatedPosition = vec2(
     scaledPosition.x * u_rotation.y +
        scaledPosition.y * u_rotation.x,
     scaledPosition.y * u_rotation.y -
        scaledPosition.x * u_rotation.x);

  // Add in the translation.
  vec2 position = rotatedPosition + u_translation;

и мы добавляем JavaScript, необходимый для установки масштаба при рисовании.

  ...
  var scaleLocation = gl.getUniformLocation(program, "u_scale");
  ...
  var scale = [1, 1];
  ...
  // Draw the scene.
  function drawScene() {
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Set the translation.
    gl.uniform2fv(translationLocation, translation);

    // Set the rotation.
    gl.uniform2fv(rotationLocation, rotation);

    // Set the scale.
    gl.uniform2fv(scaleLocation, scale);

    // Draw the rectangle.
    gl.drawArrays(gl.TRIANGLES, 0, 18);
  }

Следует отметить одну вещь: масштабирование на отрицательное значение переворачивает нашу геометрию. Я надеюсь, что эти последние три главы помогли понять перевод, вращение и масштаб. Далее мы рассмотрим волшебство матриц, которые объединяют все три элемента в гораздо более простую и зачастую более полезную форму.

Почему «F»?

Впервые я увидел, как кто-то использовал букву «F» на текстуре. Сама буква «F» не важна. Важно то, что вы можете определить его ориентацию с любого направления. Например, если бы мы использовали сердце ♥ или треугольник △, мы не могли бы определить, перевернуто ли оно по горизонтали. Круг ○ был бы еще хуже. Цветной прямоугольник, возможно, будет работать с разными цветами в каждом углу, но тогда вам придется запомнить, какой угол какой. Ориентация буквы F узнаваема мгновенно.

Любая форма, ориентацию которой вы можете определить, подойдет, я просто использовал букву F с тех пор, как впервые познакомился с этой идеей.

2D-матрицы WebGL

В последних трех главах мы рассмотрели, как переносить геометрию, вращать геометрию и масштабировать геометрию. Перевод, вращение и масштабирование считаются разновидностью «трансформации». Каждое из этих преобразований требовало изменений в шейдере, и каждое из трех преобразований зависело от порядка.

Например, здесь масштаб 2, 1, поворот 30% и перевод 100, 0.

А вот перевод 100,0, поворот 30% и масштаб 2,1

Результаты совершенно разные. Хуже того, если бы нам понадобился второй пример, нам пришлось бы написать другой шейдер, который применял бы перемещение, вращение и масштабирование в новом желаемом порядке. Ну, некоторые люди, намного умнее меня, поняли, что то же самое можно делать с помощью матричной математики. Для 2d мы используем матрицу 3x3. Матрица 3x3 похожа на сетку из 9 ячеек.

1.0	2.0	3.0
4.0	5.0	6.0
7.0	8.0	9,0

Чтобы выполнить математические вычисления, мы умножаем позиции вниз по столбцам матрицы и суммируем результаты. Наши позиции имеют только два значения: x и y, но для выполнения математических вычислений нам нужны три значения, поэтому мы будем использовать 1 в качестве третьего значения. в этом случае наш результат будет

newX = x * 1.0 + y * 4.0 + 1 * 7.0

newY = x * 2.0 + y * 5.0 + 1 * 8.0

extra = x * 3.0 + y * 6.0 + 1 * 9.0

Вы, вероятно, смотрите на это и думаете: «В ЧЕМ ДЕЛО». Ну, давайте предположим, что у нас есть перевод. Мы назовем сумму, которую хотим перевести, tx и ty. Давайте сделаем такую матрицу

1.0	0,0	0,0
0,0	1.0	0,0
Техас	ты	1.0

А теперь проверь это

newX = x * 1.0 + y * 0.0 + 1 * tx

newY = x * 0.0 + y * 1.0 + 1 * ty

extra = x * 0.0 + y * 0.0 + 1 * 1

Если вы помните свою алгебру, мы можем удалить любое место, которое умножается на ноль. Умножение на 1 фактически ничего не дает, поэтому давайте упростим, чтобы увидеть, что происходит.

newX = x + tx;
newY = y + ty;

А лишнее нас не особо волнует. Это удивительно похоже на код перевода из нашего примера перевода. Аналогично сделаем вращение. Как мы указывали в статье о вращении, нам просто нужны синус и косинус угла, на который мы хотим повернуть.

s = Math.sin(angleToRotateInRadians);
c = Math.cos(angleToRotateInRadians);

И строим такую матрицу

с	-с	0,0
с	с	0,0
0,0	0,0	1.0

Применяя матрицу, мы получаем это

newX = x * c + y * s + 1 * 0

newY = x * -s + y * c + 1 * 0

extra = x * 0.0 + y * 0.0 + 1 * 1

Затемняя все, умножаем на 0 и 1, получаем

newX = x *  c + y * s;
newY = x * -s + y * c;

Именно это и было в нашей выборке ротации. И наконец, масштаб. Мы назовем наши два масштабных коэффициента sx и sy. И построим такую матрицу.

сх	0,0	0,0
0,0	си	0,0
0,0	0,0	1.0

Применяя матрицу, мы получаем это

newX = x * sx + y * 0 + 1 * 0

newY = x * 0 + y * sy + 1 * 0

extra = x * 0.0 + y * 0.0 + 1 * 1

что на самом деле

newX = x * sx;
newY = y * sy;

Это то же самое, что и наш образец масштабирования. Теперь я уверен, что вы все еще думаете. Ну и что? Какой смысл. Кажется, это слишком много работы, чтобы сделать то же самое, что мы уже делали? Вот тут-то и начинается волшебство. Оказывается, мы можем перемножать матрицы и применять все преобразования одновременно. Предположим, у нас есть функция matrixMultiply , которая принимает две матрицы, умножает их и возвращает результат. Чтобы было понятнее, давайте создадим функции для построения матриц перемещения, вращения и масштабирования.

function makeTranslation(tx, ty) {
  return [
    1, 0, 0,
    0, 1, 0,
    tx, ty, 1
  ];
}

function makeRotation(angleInRadians) {
  var c = Math.cos(angleInRadians);
  var s = Math.sin(angleInRadians);
  return [
    c,-s, 0,
    s, c, 0,
    0, 0, 1
  ];
}

function makeScale(sx, sy) {
  return [
    sx, 0, 0,
    0, sy, 0,
    0, 0, 1
  ];
}

Теперь давайте изменим наш шейдер. Старый шейдер выглядел так

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;
uniform vec2 u_scale;

void main() {
  // Scale the positon
  vec2 scaledPosition = a_position * u_scale;

  // Rotate the position
  vec2 rotatedPosition = vec2(
     scaledPosition.x * u_rotation.y + scaledPosition.y * u_rotation.x,
     scaledPosition.y * u_rotation.y - scaledPosition.x * u_rotation.x);

  // Add in the translation.
  vec2 position = rotatedPosition + u_translation;
  ...

Наш новый шейдер будет намного проще.

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform mat3 u_matrix;

void main() {
  // Multiply the position by the matrix.
  vec2 position = (u_matrix * vec3(a_position, 1)).xy;
  ...

И вот как мы его используем

  // Draw the scene.
  function drawScene() {
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Compute the matrices
    var translationMatrix =
       makeTranslation(translation[0], translation[1]);
    var rotationMatrix = makeRotation(angleInRadians);
    var scaleMatrix = makeScale(scale[0], scale[1]);

    // Multiply the matrices.
    var matrix = matrixMultiply(scaleMatrix, rotationMatrix);
    matrix = matrixMultiply(matrix, translationMatrix);

    // Set the matrix.
    gl.uniformMatrix3fv(matrixLocation, false, matrix);

    // Draw the rectangle.
    gl.drawArrays(gl.TRIANGLES, 0, 18);
  }

Тем не менее, вы можете спросить, и что? Это не кажется большой выгодой. Но теперь, если мы хотим изменить порядок, нам не нужно писать новый шейдер. Мы можем просто изменить математику.

    ...
    // Multiply the matrices.
    var matrix = matrixMultiply(translationMatrix, rotationMatrix);
    matrix = matrixMultiply(matrix, scaleMatrix);
    ...

Возможность применять подобные матрицы особенно важна для иерархической анимации, например, рук на теле, лун на планете вокруг Солнца или ветвей на дереве. В качестве простого примера иерархической анимации давайте нарисуем букву «F» 5 раз, но каждый раз будем начинать с матрицы из предыдущей буквы «F».

  // Draw the scene.
  function drawScene() {
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Compute the matrices
    var translationMatrix = makeTranslation(translation[0], translation[1]);
    var rotationMatrix = makeRotation(angleInRadians);
    var scaleMatrix = makeScale(scale[0], scale[1]);

    // Starting Matrix.
    var matrix = makeIdentity();

    for (var i = 0; i < 5; ++i) {
      // Multiply the matrices.
      matrix = matrixMultiply(matrix, scaleMatrix);
      matrix = matrixMultiply(matrix, rotationMatrix);
      matrix = matrixMultiply(matrix, translationMatrix);

      // Set the matrix.
      gl.uniformMatrix3fv(matrixLocation, false, matrix);

      // Draw the geometry.
      gl.drawArrays(gl.TRIANGLES, 0, 18);
    }
  }

Для этого мы ввели функцию makeIdentity , которая создает единичную матрицу. Единичная матрица — это матрица, которая фактически представляет 1,0, поэтому при умножении на единицу ничего не происходит. Точно так же, как

X * 1 = X

тоже так

matrixX * identity = matrixX

Вот код для создания единичной матрицы.

function makeIdentity() {
  return [
    1, 0, 0,
    0, 1, 0,
    0, 0, 1
  ];
}

Еще один пример. В каждом примере буква «F» вращается вокруг верхнего левого угла. Это потому, что используемые нами математические вычисления всегда вращаются вокруг начала координат, а верхний левый угол нашей буквы «F» находится в начале координат (0, 0). Но теперь, поскольку мы можем выполнять матричные математические вычисления и выбирать порядок преобразования применяются, мы можем переместить начало координат до того, как будут применены остальные преобразования.

    // make a matrix that will move the origin of the 'F' to
    // its center.
    var moveOriginMatrix = makeTranslation(-50, -75);
    ...

    // Multiply the matrices.
    var matrix = matrixMultiply(moveOriginMatrix, scaleMatrix);
    matrix = matrixMultiply(matrix, rotationMatrix);
    matrix = matrixMultiply(matrix, translationMatrix);

Используя эту технику, вы можете вращать или масштабировать изображение из любой точки. Теперь вы знаете, как Photoshop или Flash позволяют перемещать точку вращения. Давайте сойдем с ума еще больше. Если вы вернетесь к первой статье об основах WebGL, вы, возможно, помните, что в шейдере есть код для преобразования пикселей в пространство отсечения, который выглядит следующим образом.

  ...
  // convert the rectangle from pixels to 0.0 to 1.0
  vec2 zeroToOne = position / u_resolution;

  // convert from 0->1 to 0->2
  vec2 zeroToTwo = zeroToOne * 2.0;

  // convert from 0->2 to -1->+1 (clipspace)
  vec2 clipSpace = zeroToTwo - 1.0;

  gl_Position = vec4(clipSpace * vec2(1, -1), 0, 1);

Если вы посмотрите на каждый из этих шагов по очереди, первый шаг «преобразование пикселей из 0,0 в 1,0» на самом деле является операцией масштабирования. Вторая также является масштабной операцией. Следующий — перевод, а самый последний масштабирует Y на -1. На самом деле мы можем сделать все это в матрице, которую передаем в шейдер. Мы могли бы создать две матрицы масштабирования: одну для масштабирования на 1,0/разрешение, другую для масштабирования на 2,0, третью для преобразования на -1,0, -1,0 и четвертую для масштабирования Y на -1, а затем умножить их все вместе, но вместо этого, потому что Математика проста, мы просто создадим функцию, которая напрямую создает матрицу «проекции» для заданного разрешения.

function make2DProjection(width, height) {
  // Note: This matrix flips the Y axis so that 0 is at the top.
  return [
    2 / width, 0, 0,
    0, -2 / height, 0,
    -1, 1, 1
  ];
}

Теперь мы можем еще больше упростить шейдер. Вот весь новый вершинный шейдер.

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform mat3 u_matrix;

void main() {
  // Multiply the position by the matrix.
  gl_Position = vec4((u_matrix * vec3(a_position, 1)).xy, 0, 1);
}
</script>

А в JavaScript нам нужно умножить на матрицу проекции

  // Draw the scene.
  function drawScene() {
    ...
    // Compute the matrices
    var projectionMatrix =
       make2DProjection(canvas.width, canvas.height);
    ...

    // Multiply the matrices.
    var matrix = matrixMultiply(scaleMatrix, rotationMatrix);
    matrix = matrixMultiply(matrix, translationMatrix);
    matrix = matrixMultiply(matrix, projectionMatrix);
    ...
  }

Мы также удалили код, устанавливающий разрешение. На этом последнем шаге мы перешли от довольно сложного шейдера с 6-7 шагами к очень простому шейдеру, состоящему всего из 1 шага, и все это благодаря магии матричной математики.

Я надеюсь, что эта статья помогла прояснить матричную математику. Дальше я перейду к 3D. В трехмерной матричной математике используются те же принципы и методы. Я начал с 2D, чтобы, надеюсь, было проще понять.