WebGL 2D অনুবাদ
আমরা 3D তে যাওয়ার আগে আসুন 2D এর সাথে আরও কিছুক্ষণ ধরে থাকি। আমার সাথে সহ্য করুন. এই নিবন্ধটি কারো কারো কাছে অত্যন্ত সুস্পষ্ট মনে হতে পারে তবে আমি কয়েকটি নিবন্ধে একটি বিন্দু পর্যন্ত তৈরি করব।
এই নিবন্ধটি WebGL ফান্ডামেন্টাল দিয়ে শুরু হওয়া একটি সিরিজের ধারাবাহিকতা। আপনি যদি এটি না পড়ে থাকেন তবে আমি আপনাকে অন্তত প্রথম অধ্যায়টি পড়ার পরামর্শ দিচ্ছি তারপর এখানে ফিরে আসুন। অনুবাদ হল কিছু অভিনব গণিতের নাম যার মূলত অর্থ "সরানো" কিছু। আমি মনে করি একটি বাক্যকে ইংরেজি থেকে জাপানি ভাষায় স্থানান্তর করাও মানানসই কিন্তু এই ক্ষেত্রে আমরা জ্যামিতি সরানোর কথা বলছি। প্রথম পোস্টে আমরা যে নমুনা কোডটি দিয়ে শেষ করেছি তা ব্যবহার করে আপনি সেটআয়তক্ষেত্রে পাস করা মান পরিবর্তন করে সহজেই আমাদের আয়তক্ষেত্রটি অনুবাদ করতে পারেন? আমাদের পূর্ববর্তী নমুনার উপর ভিত্তি করে এখানে একটি নমুনা।
// First lets make some variables
// to hold the translation of the rectangle
var translation = [0, 0];
// then let's make a function to
// re-draw everything. We can call this
// function after we update the translation.
// Draw the scene.
function drawScene() {
// Clear the canvas.
gl.clear(gl.COLOR_BUFFER_BIT);
// Setup a rectangle
setRectangle(gl, translation[0], translation[1], width, height);
// Draw the rectangle.
gl.drawArrays(gl.TRIANGLES, 0, 6);
}
এখন পর্যন্ত তাই ভাল. কিন্তু এখন কল্পনা করুন আমরা আরও জটিল আকার দিয়ে একই জিনিস করতে চেয়েছিলাম। ধরা যাক আমরা একটি 'F' আঁকতে চেয়েছিলাম যাতে 6টি ত্রিভুজ থাকে।

ওয়েল, নিম্নলিখিত বর্তমান কোড আমাদের সেটআরেকটাঙ্গলকে এইরকম আরও কিছুতে পরিবর্তন করতে হবে।
// Fill the buffer with the values that define a letter 'F'.
function setGeometry(gl, x, y) {
var width = 100;
var height = 150;
var thickness = 30;
gl.bufferData(
gl.ARRAY_BUFFER,
new Float32Array([
// left column
x, y,
x + thickness, y,
x, y + height,
x, y + height,
x + thickness, y,
x + thickness, y + height,
// top rung
x + thickness, y,
x + width, y,
x + thickness, y + thickness,
x + thickness, y + thickness,
x + width, y,
x + width, y + thickness,
// middle rung
x + thickness, y + thickness * 2,
x + width * 2 / 3, y + thickness * 2,
x + thickness, y + thickness * 3,
x + thickness, y + thickness * 3,
x + width * 2 / 3, y + thickness * 2,
x + width * 2 / 3, y + thickness * 3]),
gl.STATIC_DRAW);
}
আপনি আশা করি যে ভাল স্কেল যাচ্ছে না দেখতে পারেন. আমরা যদি শত শত বা হাজার হাজার লাইনের সাথে কিছু খুব জটিল জ্যামিতি আঁকতে চাই তবে আমাদের কিছু সুন্দর জটিল কোড লিখতে হবে। তার উপরে, আমরা যখনই জাভাস্ক্রিপ্ট আঁকি তখন সমস্ত পয়েন্ট আপডেট করতে হবে। একটি সহজ উপায় আছে. শুধু জ্যামিতি আপলোড করুন এবং শেডারে অনুবাদ করুন। এখানে নতুন shader আছে
<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;
uniform vec2 u_resolution;
uniform vec2 u_translation;
void main() {
// Add in the translation.
vec2 position = a_position + u_translation;
// convert the rectangle from pixels to 0.0 to 1.0
vec2 zeroToOne = position / u_resolution;
...
এবং আমরা কোডটি একটু পুনর্গঠন করব। একটির জন্য আমাদের শুধুমাত্র একবার জ্যামিতি সেট করতে হবে।
// Fill the buffer with the values that define a letter 'F'.
function setGeometry(gl) {
gl.bufferData(
gl.ARRAY_BUFFER,
new Float32Array([
// left column
0, 0,
30, 0,
0, 150,
0, 150,
30, 0,
30, 150,
// top rung
30, 0,
100, 0,
30, 30,
30, 30,
100, 0,
100, 30,
// middle rung
30, 60,
67, 60,
30, 90,
30, 90,
67, 60,
67, 90]),
gl.STATIC_DRAW);
}
তারপরে আমরা যে অনুবাদটি করতে চাই তা আঁকার আগে আমাদের শুধু u_translation আপডেট করতে হবে।
...
var translationLocation = gl.getUniformLocation(
program, "u_translation");
...
// Set Geometry.
setGeometry(gl);
..
// Draw scene.
function drawScene() {
// Clear the canvas.
gl.clear(gl.COLOR_BUFFER_BIT);
// Set the translation.
gl.uniform2fv(translationLocation, translation);
// Draw the rectangle.
gl.drawArrays(gl.TRIANGLES, 0, 18);
}
নোটিশ setGeometry শুধুমাত্র একবার বলা হয়। এটা আর drawScene এর ভিতরে নেই।
এখন আমরা যখন আঁকি তখন WebGL কার্যত সবকিছু করছে। আমরা যা করছি তা হল একটি অনুবাদ সেট করা এবং এটি আঁকতে বলা। এমনকি যদি আমাদের জ্যামিতিতে কয়েক হাজার পয়েন্ট থাকে তবে মূল কোডটি একই থাকবে।
WebGL 2D ঘূর্ণন
আমি ঠিক সামনে স্বীকার করতে যাচ্ছি আমার কোন ধারণা নেই যে আমি কীভাবে ব্যাখ্যা করব এটি অর্থপূর্ণ হবে তবে কি হেক, পাশাপাশি চেষ্টা করতে পারে।
প্রথমে আমি আপনাকে "ইউনিট সার্কেল" বলে পরিচয় করিয়ে দিতে চাই। আপনি যদি আপনার জুনিয়র হাই স্কুলের গণিত মনে রাখবেন (আমার উপর ঘুমাতে যাবেন না!) একটি বৃত্তের ব্যাসার্ধ আছে। একটি বৃত্তের ব্যাসার্ধ হল বৃত্তের কেন্দ্র থেকে প্রান্তের দূরত্ব। একক বৃত্ত হল একটি বৃত্ত যার ব্যাসার্ধ 1.0।
আপনি যদি মৌলিক 3য় শ্রেনীর গণিত থেকে মনে রাখবেন যদি আপনি কোন কিছুকে 1 দ্বারা গুণ করেন তবে এটি একই থাকে। তাই 123 * 1 = 123. বেশ মৌলিক অধিকার? ঠিক আছে, একটি একক বৃত্ত, 1.0 ব্যাসার্ধের একটি বৃত্তও 1 এর একটি রূপ। এটি একটি ঘূর্ণায়মান 1। সুতরাং আপনি এই একক বৃত্ত দ্বারা কিছু গুণ করতে পারেন এবং এটি একরকম যাদু ঘটে এবং জিনিসগুলি ঘোরানো ছাড়া 1 দ্বারা গুণ করার মতো। আমরা ইউনিট বৃত্তের যেকোনো বিন্দু থেকে সেই X এবং Y মানটি নিতে যাচ্ছি এবং আমরা আমাদের পূর্ববর্তী নমুনা থেকে তাদের দ্বারা আমাদের জ্যামিতিকে গুণ করব। এখানে আমাদের shader এর আপডেট আছে.
<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;
uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;
void main() {
// Rotate the position
vec2 rotatedPosition = vec2(
a_position.x * u_rotation.y + a_position.y * u_rotation.x,
a_position.y * u_rotation.y - a_position.x * u_rotation.x);
// Add in the translation.
vec2 position = rotatedPosition + u_translation;
এবং আমরা জাভাস্ক্রিপ্ট আপডেট করি যাতে আমরা সেই 2 টি মান পাস করতে পারি।
...
var rotationLocation = gl.getUniformLocation(program, "u_rotation");
...
var rotation = [0, 1];
..
// Draw the scene.
function drawScene() {
// Clear the canvas.
gl.clear(gl.COLOR_BUFFER_BIT);
// Set the translation.
gl.uniform2fv(translationLocation, translation);
// Set the rotation.
gl.uniform2fv(rotationLocation, rotation);
// Draw the rectangle.
gl.drawArrays(gl.TRIANGLES, 0, 18);
}
কেন এটা কাজ করে? আচ্ছা, গণিত দেখুন।
rotatedX = a_position.x * u_rotation.y + a_position.y * u_rotation.x;
rotatedY = a_position.y * u_rotation.y - a_position.x * u_rotation.x;
চলুন আপনার একটি আয়তক্ষেত্র আছে এবং আপনি এটি ঘোরাতে চান. আপনি এটি ঘোরানো শুরু করার আগে উপরের ডান কোণে 3.0, 9.0। 12 টা থেকে ঘড়ির কাঁটার দিকে 30 ডিগ্রি ইউনিট বৃত্তের একটি বিন্দু বাছাই করা যাক।
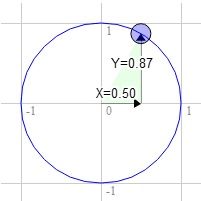
বৃত্তের অবস্থান 0.50 এবং 0.87
3.0 * 0.87 + 9.0 * 0.50 = 7.1
9.0 * 0.87 - 3.0 * 0.50 = 6.3
যে ঠিক যেখানে আমরা এটা প্রয়োজন

ঘড়ির কাঁটার দিকে 60 ডিগ্রি একই
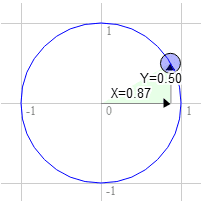
বৃত্তের অবস্থান 0.87 এবং 0.50
3.0 * 0.50 + 9.0 * 0.87 = 9.3
9.0 * 0.50 - 3.0 * 0.87 = 1.9
আপনি দেখতে পাচ্ছেন যে আমরা সেই বিন্দুটিকে ঘড়ির কাঁটার দিকে ডানদিকে ঘোরানোর সাথে সাথে X মান বড় হয় এবং Y ছোট হয়ে যায়। 90 ডিগ্রী অতিক্রম করলে X আবার ছোট হতে শুরু করবে এবং Y বড় হতে শুরু করবে। যে প্যাটার্ন আমাদের ঘূর্ণন দেয়. একটি ইউনিট বৃত্তের বিন্দুর জন্য আরেকটি নাম আছে। তারা সাইন এবং কোসাইন কল করছি. সুতরাং যেকোন প্রদত্ত কোণের জন্য আমরা এইভাবে সাইন এবং কোসাইন দেখতে পারি।
function printSineAndCosineForAnAngle(angleInDegrees) {
var angleInRadians = angleInDegrees * Math.PI / 180;
var s = Math.sin(angleInRadians);
var c = Math.cos(angleInRadians);
console.log("s = " + s + " c = " + c);
}
আপনি যদি কোডটি আপনার জাভাস্ক্রিপ্ট কনসোলে অনুলিপি এবং পেস্ট করেন এবং printSineAndCosignForAngle(30) টাইপ করেন তবে আপনি দেখতে পাচ্ছেন এটি s = 0.49 c= 0.87 প্রিন্ট করছে (দ্রষ্টব্য: আমি সংখ্যাগুলিকে বৃত্তাকার করেছি।) আপনি যদি এটি সব একসাথে রাখেন তবে আপনি আপনার জ্যামিতিকে আপনার ইচ্ছামত যেকোন কোণে ঘোরাতে পারবেন। আপনি যে কোণে ঘোরাতে চান তার সাইন এবং কোসাইনে ঘূর্ণন সেট করুন।
...
var angleInRadians = angleInDegrees * Math.PI / 180;
rotation[0] = Math.sin(angleInRadians);
rotation[1] = Math.cos(angleInRadians);
আমি আশা করি যে কিছু অর্থপূর্ণ হয়েছে. পরবর্তী একটি সহজ এক. স্কেল
রেডিয়ান কি?
রেডিয়ান হল পরিমাপের একক যা বৃত্ত, ঘূর্ণন এবং কোণ সহ ব্যবহৃত হয়। যেমন আমরা দূরত্বকে ইঞ্চি, গজ, মিটার ইত্যাদিতে পরিমাপ করতে পারি আমরা ডিগ্রী বা রেডিয়ানে কোণ পরিমাপ করতে পারি।
আপনি সম্ভবত সচেতন যে মেট্রিক পরিমাপের সাথে গণিত ইম্পেরিয়াল পরিমাপের গণিতের চেয়ে সহজ। ইঞ্চি থেকে ফুটে যেতে আমরা 12 দিয়ে ভাগ করি। ইঞ্চি থেকে গজ পর্যন্ত যেতে আমরা 36 দিয়ে ভাগ করি। আমি আপনার সম্পর্কে জানি না কিন্তু আমি আমার মাথায় 36 দিয়ে ভাগ করতে পারি না। মেট্রিকের সাথে এটি অনেক সহজ। মিলিমিটার থেকে সেন্টিমিটারে যেতে আমরা 10 দিয়ে ভাগ করি। মিলিমিটার থেকে মিটারে আমরা 1000 দিয়ে ভাগ করি। আমি আমার মাথায় 1000 দিয়ে ভাগ করতে পারি ।
রেডিয়ান বনাম ডিগ্রী একই রকম। ডিগ্রি গণিতকে কঠিন করে তোলে। রেডিয়ান গণিতকে সহজ করে তোলে। একটি বৃত্তে 360 ডিগ্রী আছে কিন্তু শুধুমাত্র 2π রেডিয়ান আছে। সুতরাং একটি পূর্ণ মোড় হল 2π রেডিয়ান। অর্ধেক টার্ন হল π রেডিয়ান। একটি 1/4 টার্ন, অর্থাৎ 90 ডিগ্রি হল π/2 রেডিয়ান। সুতরাং আপনি যদি কিছু 90 ডিগ্রি ঘোরাতে চান তবে শুধুমাত্র Math.PI * 0.5 ব্যবহার করুন। আপনি যদি এটিকে 45 ডিগ্রি ঘোরাতে চান Math.PI * 0.25 ইত্যাদি ব্যবহার করুন।
কোণ, বৃত্ত বা ঘূর্ণন জড়িত প্রায় সমস্ত গণিত খুব সহজভাবে কাজ করে যদি আপনি রেডিয়ানে চিন্তা করা শুরু করেন। তাই এটি চেষ্টা করুন. রেডিয়ান ব্যবহার করুন, UI ডিসপ্লে ছাড়া ডিগ্রী নয়।
WebGL 2D স্কেল
স্কেলিং অনুবাদের মতোই সহজ।
আমরা আমাদের পছন্দসই স্কেল দ্বারা অবস্থানকে গুণ করি। এখানে আমাদের আগের নমুনা থেকে পরিবর্তন আছে.
<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;
uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;
uniform vec2 u_scale;
void main() {
// Scale the positon
vec2 scaledPosition = a_position * u_scale;
// Rotate the position
vec2 rotatedPosition = vec2(
scaledPosition.x * u_rotation.y +
scaledPosition.y * u_rotation.x,
scaledPosition.y * u_rotation.y -
scaledPosition.x * u_rotation.x);
// Add in the translation.
vec2 position = rotatedPosition + u_translation;
এবং আমরা আঁকার সময় স্কেল সেট করার জন্য প্রয়োজনীয় জাভাস্ক্রিপ্ট যোগ করি।
...
var scaleLocation = gl.getUniformLocation(program, "u_scale");
...
var scale = [1, 1];
...
// Draw the scene.
function drawScene() {
// Clear the canvas.
gl.clear(gl.COLOR_BUFFER_BIT);
// Set the translation.
gl.uniform2fv(translationLocation, translation);
// Set the rotation.
gl.uniform2fv(rotationLocation, rotation);
// Set the scale.
gl.uniform2fv(scaleLocation, scale);
// Draw the rectangle.
gl.drawArrays(gl.TRIANGLES, 0, 18);
}
একটি বিষয় লক্ষ্য করা যায় যে একটি নেতিবাচক মান দ্বারা স্কেলিং আমাদের জ্যামিতি উল্টে দেয়। আমি আশা করি এই শেষ 3টি অধ্যায় অনুবাদ, ঘূর্ণন এবং স্কেল বোঝার জন্য সহায়ক ছিল। এরপরে আমরা ম্যাট্রিক্সের ম্যাজিকটি নিয়ে যাব যা এই তিনটিকে অনেক সহজ এবং প্রায়শই আরও দরকারী ফর্মে একত্রিত করে।
কেন একটি 'এফ'?
প্রথমবার আমি কাউকে 'এফ' ব্যবহার করতে দেখেছি একটি টেক্সচারে। 'এফ' নিজেই গুরুত্বপূর্ণ নয়। যেটা গুরুত্বপূর্ণ তা হল আপনি যে কোন দিক থেকে এর ওরিয়েন্টেশন বলতে পারেন। যদি আমরা একটি হৃদয় ♥ বা একটি ত্রিভুজ ব্যবহার করি △ উদাহরণস্বরূপ আমরা বলতে পারি না এটি অনুভূমিকভাবে উল্টানো হয়েছে কিনা। একটি বৃত্ত ○ আরও খারাপ হবে৷ একটি রঙিন আয়তক্ষেত্র তর্কযোগ্যভাবে প্রতিটি কোণে বিভিন্ন রঙের সাথে কাজ করবে কিন্তু তারপরে আপনাকে মনে রাখতে হবে কোনটি কোনটি ছিল। একটি F এর অভিযোজন অবিলম্বে স্বীকৃত হয়.

যে কোনো আকৃতি যা আপনি বলতে পারেন তার অভিযোজন কাজ করবে, আমি 'F' ব্যবহার করেছি যখন থেকে আমি 'প্রথম' ধারণাটির সাথে পরিচয় করিয়েছিলাম।
WebGL 2D ম্যাট্রিক্স
শেষ 3 অধ্যায়ে আমরা জ্যামিতি, জ্যামিতি ঘোরান, এবং জ্যামিতি স্কেল কিভাবে অনুবাদ করতে হয় তা দেখেছি। অনুবাদ, ঘূর্ণন এবং স্কেল প্রতিটি 'রূপান্তর' একটি প্রকার হিসাবে বিবেচিত হয়। এই রূপান্তরগুলির প্রতিটিতে শেডারে পরিবর্তনের প্রয়োজন ছিল এবং 3টি রূপান্তরের প্রতিটিই ছিল অর্ডার নির্ভর।
উদাহরণস্বরূপ এখানে 2, 1 এর একটি স্কেল, 30% এর ঘূর্ণন এবং 100, 0 এর অনুবাদ।

এবং এখানে 100,0 এর একটি অনুবাদ, 30% এর ঘূর্ণন এবং 2, 1 এর স্কেল রয়েছে

ফলাফল সম্পূর্ণ ভিন্ন। আরও খারাপ, যদি আমাদের দ্বিতীয় উদাহরণের প্রয়োজন হয় তবে আমাদের একটি ভিন্ন শেডার লিখতে হবে যা আমাদের নতুন পছন্দসই ক্রমে অনুবাদ, ঘূর্ণন এবং স্কেল প্রয়োগ করে। ঠিক আছে, কিছু লোক আমার চেয়ে বেশি স্মার্ট, বুঝতে পেরেছে যে আপনি ম্যাট্রিক্স গণিত দিয়ে একই জিনিস করতে পারেন। 2d এর জন্য আমরা একটি 3x3 ম্যাট্রিক্স ব্যবহার করি। একটি 3x3 ম্যাট্রিক্স 9টি বাক্স সহ গ্রিডের মতো।
| 1.0 | 2.0 | 3.0 |
| 4.0 | 5.0 | 6.0 |
| 7.0 | ৮.০ | 9.0 |
গণিত করার জন্য আমরা ম্যাট্রিক্সের কলামের নিচে অবস্থানটি গুণ করি এবং ফলাফল যোগ করি। আমাদের অবস্থানের শুধুমাত্র 2টি মান আছে, x এবং y কিন্তু এই গণিতটি করতে আমাদের 3টি মান প্রয়োজন তাই আমরা তৃতীয় মানের জন্য 1 ব্যবহার করব। এই ক্ষেত্রে আমাদের ফলাফল হবে
newX = x * 1.0 + y * 4.0 + 1 * 7.0
newY = x * 2.0 + y * 5.0 + 1 * 8.0
extra = x * 3.0 + y * 6.0 + 1 * 9.0
আপনি সম্ভবত এটি দেখছেন এবং "বিন্দু কি" ভাবছেন। ওয়েল, আমরা একটি অনুবাদ আছে অনুমান করা যাক. আমরা যে পরিমাণ tx এবং ty অনুবাদ করতে চাই তাকে কল করব। এর মত একটি ম্যাট্রিক্স করা যাক
| 1.0 | 0.0 | 0.0 |
| 0.0 | 1.0 | 0.0 |
| tx | ty | 1.0 |
এবং এখন এটা চেক আউট
newX = x * 1.0 + y * 0.0 + 1 * tx
newY = x * 0.0 + y * 1.0 + 1 * ty
extra = x * 0.0 + y * 0.0 + 1 * 1
আপনি যদি আপনার বীজগণিত মনে রাখবেন, আমরা শূন্য দ্বারা গুণিত যে কোনো স্থান মুছে ফেলতে পারি। কার্যকরভাবে 1 দ্বারা গুণ করলে কিছুই হয় না তাই আসুন সহজ করে দেখি কি ঘটছে
newX = x + tx;
newY = y + ty;
এবং অতিরিক্ত আমরা সত্যিই যত্ন না. এটি আশ্চর্যজনকভাবে আমাদের অনুবাদ উদাহরণ থেকে অনুবাদ কোডের মতো দেখাচ্ছে৷ একইভাবে এর ঘূর্ণন করা যাক. যেমন আমরা ঘূর্ণন পোস্টে উল্লেখ করেছি যে আমরা যে কোণে ঘোরাতে চাই তার সাইন এবং কোসাইন প্রয়োজন।
s = Math.sin(angleToRotateInRadians);
c = Math.cos(angleToRotateInRadians);
এবং আমরা এই মত একটি ম্যাট্রিক্স নির্মাণ
| গ | -s | 0.0 |
| s | গ | 0.0 |
| 0.0 | 0.0 | 1.0 |
ম্যাট্রিক্স প্রয়োগ করলে আমরা এটি পাই
newX = x * c + y * s + 1 * 0
newY = x * -s + y * c + 1 * 0
extra = x * 0.0 + y * 0.0 + 1 * 1
সমস্ত ব্ল্যাক আউট 0s এবং 1s দ্বারা গুণিত আমরা পেতে
newX = x * c + y * s;
newY = x * -s + y * c;
যা আমরা আমাদের ঘূর্ণন নমুনা ছিল ঠিক কি. এবং সবশেষে স্কেল। আমরা আমাদের 2 স্কেল ফ্যাক্টর sx এবং sy কল করব এবং আমরা এইভাবে একটি ম্যাট্রিক্স তৈরি করব
| sx | 0.0 | 0.0 |
| 0.0 | sy | 0.0 |
| 0.0 | 0.0 | 1.0 |
ম্যাট্রিক্স প্রয়োগ করলে আমরা এটি পাই
newX = x * sx + y * 0 + 1 * 0
newY = x * 0 + y * sy + 1 * 0
extra = x * 0.0 + y * 0.0 + 1 * 1
যা সত্যিই
newX = x * sx;
newY = y * sy;
যা আমাদের স্কেলিং নমুনা হিসাবে একই. এখন আমি নিশ্চিত যে আপনি এখনও ভাবছেন। তাই কি? কি ব্যাপার. যে কাজ অনেক মত মনে হচ্ছে ঠিক একই জিনিস আমরা ইতিমধ্যে করছি? এখানেই জাদু আসে। দেখা যাচ্ছে আমরা ম্যাট্রিক্সকে একসাথে গুণ করতে পারি এবং সব রূপান্তর একবারে প্রয়োগ করতে পারি। ধরা যাক আমাদের ফাংশন আছে, matrixMultiply , যা দুটি ম্যাট্রিক্স নেয়, তাদের গুণ করে এবং ফলাফল দেয়। বিষয়গুলিকে আরও পরিষ্কার করতে আসুন অনুবাদ, ঘূর্ণন এবং স্কেল এর জন্য ম্যাট্রিক্স তৈরি করার ফাংশন তৈরি করি।
function makeTranslation(tx, ty) {
return [
1, 0, 0,
0, 1, 0,
tx, ty, 1
];
}
function makeRotation(angleInRadians) {
var c = Math.cos(angleInRadians);
var s = Math.sin(angleInRadians);
return [
c,-s, 0,
s, c, 0,
0, 0, 1
];
}
function makeScale(sx, sy) {
return [
sx, 0, 0,
0, sy, 0,
0, 0, 1
];
}
এখন আমাদের shader পরিবর্তন করা যাক. বুড়ো শ্যাডারকে এমন লাগছিল
<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;
uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;
uniform vec2 u_scale;
void main() {
// Scale the positon
vec2 scaledPosition = a_position * u_scale;
// Rotate the position
vec2 rotatedPosition = vec2(
scaledPosition.x * u_rotation.y + scaledPosition.y * u_rotation.x,
scaledPosition.y * u_rotation.y - scaledPosition.x * u_rotation.x);
// Add in the translation.
vec2 position = rotatedPosition + u_translation;
...
আমাদের নতুন শেডার অনেক সহজ হবে।
<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;
uniform vec2 u_resolution;
uniform mat3 u_matrix;
void main() {
// Multiply the position by the matrix.
vec2 position = (u_matrix * vec3(a_position, 1)).xy;
...
এবং এখানে আমরা কিভাবে এটি ব্যবহার
// Draw the scene.
function drawScene() {
// Clear the canvas.
gl.clear(gl.COLOR_BUFFER_BIT);
// Compute the matrices
var translationMatrix =
makeTranslation(translation[0], translation[1]);
var rotationMatrix = makeRotation(angleInRadians);
var scaleMatrix = makeScale(scale[0], scale[1]);
// Multiply the matrices.
var matrix = matrixMultiply(scaleMatrix, rotationMatrix);
matrix = matrixMultiply(matrix, translationMatrix);
// Set the matrix.
gl.uniformMatrix3fv(matrixLocation, false, matrix);
// Draw the rectangle.
gl.drawArrays(gl.TRIANGLES, 0, 18);
}
তবুও, আপনি জিজ্ঞাসা করা হতে পারে, তাই কি? এটা খুব একটা লাভ বলে মনে হচ্ছে না। কিন্তু, এখন যদি আমরা ক্রম পরিবর্তন করতে চাই তবে আমাদের একটি নতুন শেডার লিখতে হবে না। আমরা শুধু গণিত পরিবর্তন করতে পারেন.
...
// Multiply the matrices.
var matrix = matrixMultiply(translationMatrix, rotationMatrix);
matrix = matrixMultiply(matrix, scaleMatrix);
...
এই ধরনের ম্যাট্রিক্স প্রয়োগ করতে পারা বিশেষ করে শরীরের উপর অস্ত্র, সূর্যের চারপাশে একটি গ্রহে চাঁদ, বা গাছের ডালগুলির মতো শ্রেণীবদ্ধ অ্যানিমেশনের জন্য গুরুত্বপূর্ণ। অনুক্রমিক অ্যানিমেশনের একটি সাধারণ উদাহরণের জন্য আমাদের 'F' 5 বার আঁকা যাক কিন্তু প্রতিবার আগের 'F' থেকে ম্যাট্রিক্স দিয়ে শুরু করা যাক।
// Draw the scene.
function drawScene() {
// Clear the canvas.
gl.clear(gl.COLOR_BUFFER_BIT);
// Compute the matrices
var translationMatrix = makeTranslation(translation[0], translation[1]);
var rotationMatrix = makeRotation(angleInRadians);
var scaleMatrix = makeScale(scale[0], scale[1]);
// Starting Matrix.
var matrix = makeIdentity();
for (var i = 0; i < 5; ++i) {
// Multiply the matrices.
matrix = matrixMultiply(matrix, scaleMatrix);
matrix = matrixMultiply(matrix, rotationMatrix);
matrix = matrixMultiply(matrix, translationMatrix);
// Set the matrix.
gl.uniformMatrix3fv(matrixLocation, false, matrix);
// Draw the geometry.
gl.drawArrays(gl.TRIANGLES, 0, 18);
}
}
এটি করার জন্য আমরা ফাংশনটি চালু করেছি, makeIdentity , যা একটি পরিচয় ম্যাট্রিক্স তৈরি করে। একটি পরিচয় ম্যাট্রিক্স হল একটি ম্যাট্রিক্স যা কার্যকরভাবে 1.0 প্রতিনিধিত্ব করে যাতে আপনি পরিচয় দ্বারা গুণ করলে কিছুই ঘটে না। ঠিক মত
X * 1 = X
তাই খুব
matrixX * identity = matrixX
এখানে একটি আইডেন্টিটি ম্যাট্রিক্স তৈরি করার কোড আছে।
function makeIdentity() {
return [
1, 0, 0,
0, 1, 0,
0, 0, 1
];
}
আরও একটি উদাহরণ, এখন পর্যন্ত প্রতিটি নমুনায় আমাদের 'F' তার উপরের বাম কোণে ঘোরে। এর কারণ হল আমরা যে গণিতটি ব্যবহার করছি তা সর্বদা উৎপত্তির চারপাশে ঘোরে এবং আমাদের 'F'-এর উপরের বাম কোণটি উৎপত্তিস্থলে রয়েছে, (0, 0) কিন্তু এখন, যেহেতু আমরা ম্যাট্রিক্স গণিত করতে পারি এবং আমরা যে ক্রমটি রূপান্তর প্রয়োগ করতে পারি সেটি বেছে নিতে পারি, বাকি রূপান্তরগুলি প্রয়োগ করার আগে আমরা মূলটিকে সরাতে পারি।
// make a matrix that will move the origin of the 'F' to
// its center.
var moveOriginMatrix = makeTranslation(-50, -75);
...
// Multiply the matrices.
var matrix = matrixMultiply(moveOriginMatrix, scaleMatrix);
matrix = matrixMultiply(matrix, rotationMatrix);
matrix = matrixMultiply(matrix, translationMatrix);
সেই কৌশলটি ব্যবহার করে আপনি যেকোনো বিন্দু থেকে ঘোরাতে বা স্কেল করতে পারেন। এখন আপনি জানেন কিভাবে ফটোশপ বা ফ্ল্যাশ আপনাকে ঘূর্ণন বিন্দু সরাতে দেয়। চল আরো পাগল হয়ে যাই। আপনি যদি WebGL ফান্ডামেন্টালের প্রথম নিবন্ধে ফিরে যান তাহলে আপনার মনে হতে পারে আমাদের কাছে পিক্সেল থেকে ক্লিপস্পেসে রূপান্তর করার জন্য শেডারে কোড আছে যা দেখতে এইরকম।
...
// convert the rectangle from pixels to 0.0 to 1.0
vec2 zeroToOne = position / u_resolution;
// convert from 0->1 to 0->2
vec2 zeroToTwo = zeroToOne * 2.0;
// convert from 0->2 to -1->+1 (clipspace)
vec2 clipSpace = zeroToTwo - 1.0;
gl_Position = vec4(clipSpace * vec2(1, -1), 0, 1);
আপনি যদি প্রতিটি ধাপে ঘুরে দেখেন, প্রথম ধাপ, "পিক্সেল থেকে 0.0 থেকে 1.0 এ রূপান্তর করুন", সত্যিই একটি স্কেল অপারেশন। দ্বিতীয়টিও একটি স্কেল অপারেশন। পরেরটি একটি অনুবাদ এবং একেবারে শেষ স্কেল Y দ্বারা -1। আমরা আসলে যে সব করতে পারেন ম্যাট্রিক্স আমরা shader মধ্যে পাস. আমরা 2টি স্কেল ম্যাট্রিক্স তৈরি করতে পারি, একটি 1.0/রেজোলিউশন দ্বারা স্কেল করতে, আরেকটি 2.0 দ্বারা স্কেল করতে, একটি 3য়টি -1.0,-1.0 দ্বারা অনুবাদ করতে এবং চতুর্থটি Y স্কেল -1 দ্বারা অনুবাদ করতে পারি তারপর সেগুলিকে একসাথে গুণ করি কিন্তু পরিবর্তে, কারণ গণিতটি সহজ, আমরা কেবল একটি ফাংশন তৈরি করব যা সরাসরি প্রদত্ত রেজোলিউশনের জন্য একটি 'প্রজেকশন' ম্যাট্রিক্স তৈরি করবে।
function make2DProjection(width, height) {
// Note: This matrix flips the Y axis so that 0 is at the top.
return [
2 / width, 0, 0,
0, -2 / height, 0,
-1, 1, 1
];
}
এখন আমরা শেডারটিকে আরও সহজ করতে পারি। এখানে সম্পূর্ণ নতুন ভার্টেক্স শেডার আছে।
<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;
uniform mat3 u_matrix;
void main() {
// Multiply the position by the matrix.
gl_Position = vec4((u_matrix * vec3(a_position, 1)).xy, 0, 1);
}
</script>
এবং জাভাস্ক্রিপ্টে আমাদের প্রজেকশন ম্যাট্রিক্স দ্বারা গুন করতে হবে
// Draw the scene.
function drawScene() {
...
// Compute the matrices
var projectionMatrix =
make2DProjection(canvas.width, canvas.height);
...
// Multiply the matrices.
var matrix = matrixMultiply(scaleMatrix, rotationMatrix);
matrix = matrixMultiply(matrix, translationMatrix);
matrix = matrixMultiply(matrix, projectionMatrix);
...
}
আমরা রেজোলিউশন সেট করে এমন কোডটিও সরিয়ে দিয়েছি। এই শেষ ধাপের মাধ্যমে আমরা 6-7 ধাপের একটি জটিল শেডার থেকে একটি খুব সাধারণ শেডারে চলে গেছি মাত্র 1 ধাপের সাথে ম্যাট্রিক্স গণিতের যাদুতে।
আমি আশা করি এই নিবন্ধটি ম্যাট্রিক্স গণিতকে রহস্যময় করতে সাহায্য করেছে। আমি পরবর্তী 3D-এ চলে যাব। 3D ম্যাট্রিক্সে গণিত একই নীতি এবং ব্যবহার অনুসরণ করে। আমি 2D দিয়ে শুরু করেছি আশাকরি এটি বুঝতে সহজ।


