Tradução 2D do WebGL
Antes de passarmos para o 3D, vamos continuar com o 2D por um tempo. Aguarde um pouco. Este artigo pode parecer extremamente óbvio para alguns, mas vou chegar a um ponto em alguns artigos.
Este artigo é a continuação de uma série que começa com Noções básicas do WebGL. Se você ainda não leu, sugiro que leia pelo menos o primeiro capítulo e volte aqui. A tradução é um nome matemático sofisticado que significa basicamente "mover" algo. Acho que mudar uma frase do inglês para o japonês também se encaixa, mas, neste caso, estamos falando sobre mover a geometria. Usando o código de exemplo que criamos na primeira postagem, você pode traduzir nosso retângulo facilmente apenas mudando os valores transmitidos para setRectangle, certo? Confira um exemplo baseado na nossa amostra anterior.
// First lets make some variables
// to hold the translation of the rectangle
var translation = [0, 0];
// then let's make a function to
// re-draw everything. We can call this
// function after we update the translation.
// Draw the scene.
function drawScene() {
// Clear the canvas.
gl.clear(gl.COLOR_BUFFER_BIT);
// Setup a rectangle
setRectangle(gl, translation[0], translation[1], width, height);
// Draw the rectangle.
gl.drawArrays(gl.TRIANGLES, 0, 6);
}
Até agora, tudo bem. Mas agora imagine que queremos fazer a mesma coisa com uma forma mais complicada. Digamos que queremos desenhar um "F" que consiste em seis triângulos como este.

Confira o código atual que precisa ser alterado para setRectangle.
// Fill the buffer with the values that define a letter 'F'.
function setGeometry(gl, x, y) {
var width = 100;
var height = 150;
var thickness = 30;
gl.bufferData(
gl.ARRAY_BUFFER,
new Float32Array([
// left column
x, y,
x + thickness, y,
x, y + height,
x, y + height,
x + thickness, y,
x + thickness, y + height,
// top rung
x + thickness, y,
x + width, y,
x + thickness, y + thickness,
x + thickness, y + thickness,
x + width, y,
x + width, y + thickness,
// middle rung
x + thickness, y + thickness * 2,
x + width * 2 / 3, y + thickness * 2,
x + thickness, y + thickness * 3,
x + thickness, y + thickness * 3,
x + width * 2 / 3, y + thickness * 2,
x + width * 2 / 3, y + thickness * 3]),
gl.STATIC_DRAW);
}
Você pode notar que isso não vai ser bem dimensionado. Se quisermos desenhar uma geometria muito complexa com centenas ou milhares de linhas, precisaremos escrever um código muito complexo. Além disso, toda vez que desenhamos, o JavaScript precisa atualizar todos os pontos. Há uma maneira mais simples. Basta fazer o upload da geometria e fazer a tradução no sombreador. Confira o novo sombreador
<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;
uniform vec2 u_resolution;
uniform vec2 u_translation;
void main() {
// Add in the translation.
vec2 position = a_position + u_translation;
// convert the rectangle from pixels to 0.0 to 1.0
vec2 zeroToOne = position / u_resolution;
...
e vamos reestruturar o código um pouco. Por exemplo, só precisamos definir a geometria uma vez.
// Fill the buffer with the values that define a letter 'F'.
function setGeometry(gl) {
gl.bufferData(
gl.ARRAY_BUFFER,
new Float32Array([
// left column
0, 0,
30, 0,
0, 150,
0, 150,
30, 0,
30, 150,
// top rung
30, 0,
100, 0,
30, 30,
30, 30,
100, 0,
100, 30,
// middle rung
30, 60,
67, 60,
30, 90,
30, 90,
67, 60,
67, 90]),
gl.STATIC_DRAW);
}
Depois, basta atualizar u_translation antes de desenhar com a tradução desejada.
...
var translationLocation = gl.getUniformLocation(
program, "u_translation");
...
// Set Geometry.
setGeometry(gl);
..
// Draw scene.
function drawScene() {
// Clear the canvas.
gl.clear(gl.COLOR_BUFFER_BIT);
// Set the translation.
gl.uniform2fv(translationLocation, translation);
// Draw the rectangle.
gl.drawArrays(gl.TRIANGLES, 0, 18);
}
O método setGeometry é chamado apenas uma vez. Ele não está mais dentro de drawScene.
Agora, quando renderizamos, o WebGL faz praticamente tudo. Estamos apenas definindo uma tradução e pedindo para ela desenhar. Mesmo que nossa geometria tenha dezenas de milhares de pontos, o código principal vai permanecer o mesmo.
Rotação 2D do WebGL
Vou admitir logo de cara que não tenho ideia se a explicação que vou dar vai fazer sentido, mas, vamos lá.
Primeiro, quero apresentar o que é chamado de "círculo unitário". Se você se lembra da matemática do ensino fundamental (não durma em cima disso!), um círculo tem um raio. O raio de um círculo é a distância entre o centro e a borda. Um círculo unitário é um círculo com um raio de 1,0.
Se você se lembra da matemática básica da terceira série, se você multiplicar algo por 1, ele vai permanecer o mesmo. Portanto, 123 * 1 = 123. Bem básico, certo? Bem, um círculo unitário, um círculo com um raio de 1,0 também é uma forma de 1. É um 1 giratório. Você pode multiplicar algo por esse círculo unitário, e isso é mais ou menos como multiplicar por 1, exceto que a mágica acontece e as coisas giram. Vamos usar os valores X e Y de qualquer ponto no círculo unitário e multiplicar nossa geometria por eles da amostra anterior. Confira as atualizações do nosso sombreador.
<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;
uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;
void main() {
// Rotate the position
vec2 rotatedPosition = vec2(
a_position.x * u_rotation.y + a_position.y * u_rotation.x,
a_position.y * u_rotation.y - a_position.x * u_rotation.x);
// Add in the translation.
vec2 position = rotatedPosition + u_translation;
E atualizamos o JavaScript para transmitir esses dois valores.
...
var rotationLocation = gl.getUniformLocation(program, "u_rotation");
...
var rotation = [0, 1];
..
// Draw the scene.
function drawScene() {
// Clear the canvas.
gl.clear(gl.COLOR_BUFFER_BIT);
// Set the translation.
gl.uniform2fv(translationLocation, translation);
// Set the rotation.
gl.uniform2fv(rotationLocation, rotation);
// Draw the rectangle.
gl.drawArrays(gl.TRIANGLES, 0, 18);
}
Por que isso funciona? Vamos analisar os números.
rotatedX = a_position.x * u_rotation.y + a_position.y * u_rotation.x;
rotatedY = a_position.y * u_rotation.y - a_position.x * u_rotation.x;
Digamos que você tenha um retângulo e queira girá-lo. Antes de começar a girar, o canto superior direito está em 3,0, 9,0. Vamos escolher um ponto no círculo unitário a 30 graus no sentido horário a partir das 12 horas.
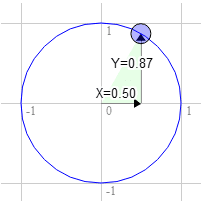
A posição no círculo é 0,50 e 0,87
3.0 * 0.87 + 9.0 * 0.50 = 7.1
9.0 * 0.87 - 3.0 * 0.50 = 6.3
É exatamente onde precisamos

O mesmo para 60 graus no sentido horário
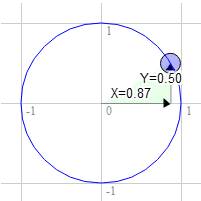
A posição no círculo é 0,87 e 0,50.
3.0 * 0.50 + 9.0 * 0.87 = 9.3
9.0 * 0.50 - 3.0 * 0.87 = 1.9
Você pode notar que, à medida que giramos esse ponto no sentido horário para a direita, o valor de X aumenta e o de Y diminui. Se continuar passando de 90 graus, X vai começar a ficar menor novamente, e Y vai começar a ficar maior. Esse padrão nos dá a rotação. Há outro nome para os pontos em um círculo unitário. Eles são chamados de seno e cosseno. Para qualquer ângulo, podemos procurar o seno e o cosseno assim.
function printSineAndCosineForAnAngle(angleInDegrees) {
var angleInRadians = angleInDegrees * Math.PI / 180;
var s = Math.sin(angleInRadians);
var c = Math.cos(angleInRadians);
console.log("s = " + s + " c = " + c);
}
Se você copiar e colar o código no console JavaScript e digitar printSineAndCosignForAngle(30), ele vai imprimir s = 0.49 c= 0.87 (observe que arredondamos os números).
Se você colocar tudo junto, poderá girar a geometria para qualquer ângulo que quiser. Basta definir a rotação para o seno e o cosseno do ângulo que você quer girar.
...
var angleInRadians = angleInDegrees * Math.PI / 180;
rotation[0] = Math.sin(angleInRadians);
rotation[1] = Math.cos(angleInRadians);
Espero que isso tenha ajudado. Agora, vamos ver um exemplo mais simples. Escale.
O que são radians?
Os radianos são uma unidade de medida usada com círculos, rotações e ângulos. Assim como podemos medir distâncias em polegadas, jardas, metros etc., podemos medir ângulos em graus ou radianos.
Você provavelmente sabe que a matemática com medidas métricas é mais fácil do que com medidas imperiais. Para converter de polegadas para pés, dividimos por 12. Para converter de polegadas para jardas, dividimos por 36. Não sei você, mas eu não consigo dividir por 36 de cabeça. Com a métrica, é muito mais fácil. Para converter milímetros em centímetros, dividimos por 10. Para converter milímetros em metros, dividimos por 1.000. Posso dividir por 1.000 mentalmente.
Radianos e graus são semelhantes. Os graus dificultam a matemática. Os radianos facilitam as contas. Há 360 graus em um círculo, mas apenas 2π radianos. Uma volta completa é igual a 2π radianos. Uma meia volta é π radianos. Um quarto de volta, ou seja, 90 graus, é π/2 radiano. Portanto, se você quiser girar algo em 90 graus, use Math.PI * 0.5. Se você quiser girar em 45 graus, use Math.PI * 0.25 etc.
Quase toda matemática que envolve ângulos, círculos ou rotações funciona de maneira muito simples se você começar a pensar em radianos. Então, tente. Use radianos, não graus, exceto em exibições de interface.
Escala 2D do WebGL
O escalonamento é tão fácil quanto a tradução.
Multiplicamos a posição pela escala desejada. Confira as mudanças da nossa amostra anterior.
<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;
uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;
uniform vec2 u_scale;
void main() {
// Scale the positon
vec2 scaledPosition = a_position * u_scale;
// Rotate the position
vec2 rotatedPosition = vec2(
scaledPosition.x * u_rotation.y +
scaledPosition.y * u_rotation.x,
scaledPosition.y * u_rotation.y -
scaledPosition.x * u_rotation.x);
// Add in the translation.
vec2 position = rotatedPosition + u_translation;
e adicionamos o JavaScript necessário para definir a escala ao desenhar.
...
var scaleLocation = gl.getUniformLocation(program, "u_scale");
...
var scale = [1, 1];
...
// Draw the scene.
function drawScene() {
// Clear the canvas.
gl.clear(gl.COLOR_BUFFER_BIT);
// Set the translation.
gl.uniform2fv(translationLocation, translation);
// Set the rotation.
gl.uniform2fv(rotationLocation, rotation);
// Set the scale.
gl.uniform2fv(scaleLocation, scale);
// Draw the rectangle.
gl.drawArrays(gl.TRIANGLES, 0, 18);
}
Uma coisa a notar é que a escalação por um valor negativo inverte nossa geometria. Esperamos que os três últimos capítulos tenham ajudado você a entender a tradução, a rotação e a escala. A seguir, vamos falar sobre a magia das matrizes que combinam os três em uma forma muito mais simples e, muitas vezes, mais útil.
Por que uma "F"?
A primeira vez que vi alguém usar um "F" foi em uma textura. O "F" em si não é importante. O importante é que você consiga identificar a orientação em qualquer direção. Se usássemos um coração ♥ ou um triângulo △, por exemplo, não seria possível saber se ele foi invertido horizontalmente. Um círculo ○ seria ainda pior. Um retângulo colorido poderia funcionar com cores diferentes em cada canto, mas você teria que lembrar qual canto era qual. A orientação de um F é reconhecida instantaneamente.

Qualquer forma que você possa indicar a orientação funcionaria. Eu usei "F" desde que me apresentaram a ideia.
Matrizes 2D do WebGL
Nos últimos três capítulos, abordamos como traduzir, girar e dimensionar geometrias. A translação, a rotação e a escala são consideradas tipos de "transformação". Cada uma dessas transformações exigia mudanças no sombreador, e cada uma das três transformações dependia da ordem.
Por exemplo, aqui está uma escala de 2, 1, rotação de 30% e translação de 100, 0.

E aqui está uma translação de 100,0, rotação de 30% e escala de 2, 1

Os resultados são completamente diferentes. Pior ainda, se precisássemos do segundo exemplo, teríamos que escrever um sombreador diferente que aplicasse a tradução, a rotação e a escala na nova ordem desejada. Bem, algumas pessoas muito mais inteligentes do que eu descobriram que é possível fazer as mesmas coisas com matemática matricial. Para 2D, usamos uma matriz 3x3. Uma matriz 3x3 é como uma grade com nove caixas.
| 1,0 | 2,0 | 3.0 |
| 4.0 | 5.0 | 6.0 |
| 7.0 | 8.0 | 9.0 |
Para fazer a matemática, multiplicamos a posição pelas colunas da matriz e somamos os resultados. Nossas posições têm apenas dois valores, x e y, mas para fazer essa matemática, precisamos de três valores. Portanto, vamos usar 1 para o terceiro valor. Nesse caso, o resultado seria
newX = x * 1.0 + y * 4.0 + 1 * 7.0
newY = x * 2.0 + y * 5.0 + 1 * 8.0
extra = x * 3.0 + y * 6.0 + 1 * 9.0
Você provavelmente está olhando para isso e pensando "PARA QUE SERVE?". Vamos supor que temos uma tradução. Vamos chamar o valor que queremos traduzir de tx e ty. Vamos criar uma matriz como esta
| 1,0 | 0,0 | 0,0 |
| 0,0 | 1,0 | 0,0 |
| tx | ty | 1,0 |
E agora, confira
newX = x * 1.0 + y * 0.0 + 1 * tx
newY = x * 0.0 + y * 1.0 + 1 * ty
extra = x * 0.0 + y * 0.0 + 1 * 1
Se você se lembra da álgebra, podemos excluir qualquer lugar que se multiplica por zero. Multiplicar por 1 não faz nada. Vamos simplificar para ver o que está acontecendo.
newX = x + tx;
newY = y + ty;
E não nos importamos com o que é extra. Isso parece surpreendentemente semelhante ao código de tradução do nosso exemplo. Da mesma forma, vamos fazer a rotação. Como apontamos na postagem sobre rotação, só precisamos do seno e do cosseno do ângulo em que queremos fazer a rotação.
s = Math.sin(angleToRotateInRadians);
c = Math.cos(angleToRotateInRadians);
E criamos uma matriz como esta
| c | -s | 0,0 |
| s | c | 0,0 |
| 0,0 | 0,0 | 1,0 |
Aplicando a matriz, temos
newX = x * c + y * s + 1 * 0
newY = x * -s + y * c + 1 * 0
extra = x * 0.0 + y * 0.0 + 1 * 1
O resultado de apagar todos os zeros e uns é
newX = x * c + y * s;
newY = x * -s + y * c;
O que é exatamente o que tínhamos na nossa amostra de rotação. E, por último, a escala. Vamos chamar nossos dois fatores de escalonamento de sx e sy E criaremos uma matriz como esta
| sx | 0,0 | 0,0 |
| 0,0 | sy | 0,0 |
| 0,0 | 0,0 | 1,0 |
Aplicando a matriz, temos
newX = x * sx + y * 0 + 1 * 0
newY = x * 0 + y * sy + 1 * 0
extra = x * 0.0 + y * 0.0 + 1 * 1
que é realmente
newX = x * sx;
newY = y * sy;
que é igual ao nosso exemplo de escalonamento.
Agora, você ainda pode estar pensando. E o que isso significa? Qual é o objetivo. Parece muito trabalho só para fazer a mesma coisa que já estávamos fazendo?
É aqui que a mágica acontece. Podemos multiplicar matrizes e aplicar todas as transformações de uma vez. Vamos supor que temos a função matrixMultiply, que recebe duas matrizes, as multiplica e retorna o resultado.
Para deixar as coisas mais claras, vamos criar funções para criar matrizes de translação, rotação e escala.
function makeTranslation(tx, ty) {
return [
1, 0, 0,
0, 1, 0,
tx, ty, 1
];
}
function makeRotation(angleInRadians) {
var c = Math.cos(angleInRadians);
var s = Math.sin(angleInRadians);
return [
c,-s, 0,
s, c, 0,
0, 0, 1
];
}
function makeScale(sx, sy) {
return [
sx, 0, 0,
0, sy, 0,
0, 0, 1
];
}
Agora vamos mudar o shader. O sombreador antigo tinha esta aparência
<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;
uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;
uniform vec2 u_scale;
void main() {
// Scale the positon
vec2 scaledPosition = a_position * u_scale;
// Rotate the position
vec2 rotatedPosition = vec2(
scaledPosition.x * u_rotation.y + scaledPosition.y * u_rotation.x,
scaledPosition.y * u_rotation.y - scaledPosition.x * u_rotation.x);
// Add in the translation.
vec2 position = rotatedPosition + u_translation;
...
Nosso novo sombreador será muito mais simples.
<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;
uniform vec2 u_resolution;
uniform mat3 u_matrix;
void main() {
// Multiply the position by the matrix.
vec2 position = (u_matrix * vec3(a_position, 1)).xy;
...
E é assim que usamos
// Draw the scene.
function drawScene() {
// Clear the canvas.
gl.clear(gl.COLOR_BUFFER_BIT);
// Compute the matrices
var translationMatrix =
makeTranslation(translation[0], translation[1]);
var rotationMatrix = makeRotation(angleInRadians);
var scaleMatrix = makeScale(scale[0], scale[1]);
// Multiply the matrices.
var matrix = matrixMultiply(scaleMatrix, rotationMatrix);
matrix = matrixMultiply(matrix, translationMatrix);
// Set the matrix.
gl.uniformMatrix3fv(matrixLocation, false, matrix);
// Draw the rectangle.
gl.drawArrays(gl.TRIANGLES, 0, 18);
}
Mas você pode estar se perguntando: e daí? Isso não parece um benefício . No entanto, agora, se quisermos mudar a ordem, não precisamos escrever um novo sombreador. Podemos mudar a matemática.
...
// Multiply the matrices.
var matrix = matrixMultiply(translationMatrix, rotationMatrix);
matrix = matrixMultiply(matrix, scaleMatrix);
...
Aplicar matrizes como essa é especialmente importante para animações hierárquicas, como braços em um corpo, luas em um planeta ao redor de um sol ou galhos em uma árvore. Para um exemplo simples de animação hierárquica, vamos desenhar nossa "F" cinco vezes, mas cada vez vamos começar com a matriz da "F" anterior.
// Draw the scene.
function drawScene() {
// Clear the canvas.
gl.clear(gl.COLOR_BUFFER_BIT);
// Compute the matrices
var translationMatrix = makeTranslation(translation[0], translation[1]);
var rotationMatrix = makeRotation(angleInRadians);
var scaleMatrix = makeScale(scale[0], scale[1]);
// Starting Matrix.
var matrix = makeIdentity();
for (var i = 0; i < 5; ++i) {
// Multiply the matrices.
matrix = matrixMultiply(matrix, scaleMatrix);
matrix = matrixMultiply(matrix, rotationMatrix);
matrix = matrixMultiply(matrix, translationMatrix);
// Set the matrix.
gl.uniformMatrix3fv(matrixLocation, false, matrix);
// Draw the geometry.
gl.drawArrays(gl.TRIANGLES, 0, 18);
}
}
Para isso, apresentamos a função makeIdentity, que cria uma matriz de identidade. Uma matriz de identidade é uma matriz que representa efetivamente 1,0, de modo que, se você multiplicar pela identidade, nada acontece. Assim como
X * 1 = X
também
matrixX * identity = matrixX
Confira o código para criar uma matriz de identidade.
function makeIdentity() {
return [
1, 0, 0,
0, 1, 0,
0, 0, 1
];
}
Mais um exemplo: em todas as amostras até agora, a letra "F" gira em torno do canto superior esquerdo. Isso acontece porque a matemática que usamos sempre gira em torno da origem, e o canto superior esquerdo do "F" está na origem, (0, 0). Mas agora, como podemos fazer cálculos de matriz e escolher a ordem em que as transformações são aplicadas, podemos mover a origem antes que o restante das transformações seja aplicado.
// make a matrix that will move the origin of the 'F' to
// its center.
var moveOriginMatrix = makeTranslation(-50, -75);
...
// Multiply the matrices.
var matrix = matrixMultiply(moveOriginMatrix, scaleMatrix);
matrix = matrixMultiply(matrix, rotationMatrix);
matrix = matrixMultiply(matrix, translationMatrix);
Usando essa técnica, você pode girar ou dimensionar de qualquer ponto. Agora você sabe como o Photoshop ou o Flash permitem mover o ponto de rotação. Vamos ficar ainda mais malucos. Se você voltar ao primeiro artigo sobre fundamentos da WebGL, vai se lembrar que temos um código no sombreador para converter de pixels para clipspace, que é parecido com este.
...
// convert the rectangle from pixels to 0.0 to 1.0
vec2 zeroToOne = position / u_resolution;
// convert from 0->1 to 0->2
vec2 zeroToTwo = zeroToOne * 2.0;
// convert from 0->2 to -1->+1 (clipspace)
vec2 clipSpace = zeroToTwo - 1.0;
gl_Position = vec4(clipSpace * vec2(1, -1), 0, 1);
Se você analisar cada uma dessas etapas, a primeira, "converter de pixels para 0,0 a 1,0", é realmente uma operação de escala. A segunda também é uma operação de escalonamento. A próxima é uma translação, e a última escala Y em -1. Podemos fazer isso na matriz que transmitimos para o sombreador. Poderíamos criar duas matrizes de escala, uma para dimensionar por 1,0/resolução, outra para dimensionar por 2,0, uma terceira para traduzir por -1,0,-1,0 e uma quarta para dimensionar Y por -1 e, em seguida, multiplicar tudo. No entanto, como a matemática é simples, vamos criar uma função que gera uma matriz de "projeção" para uma determinada resolução diretamente.
function make2DProjection(width, height) {
// Note: This matrix flips the Y axis so that 0 is at the top.
return [
2 / width, 0, 0,
0, -2 / height, 0,
-1, 1, 1
];
}
Agora podemos simplificar o sombreador ainda mais. Confira o novo sombreador de vértice.
<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;
uniform mat3 u_matrix;
void main() {
// Multiply the position by the matrix.
gl_Position = vec4((u_matrix * vec3(a_position, 1)).xy, 0, 1);
}
</script>
E no JavaScript, precisamos multiplicar pela matriz de projeção
// Draw the scene.
function drawScene() {
...
// Compute the matrices
var projectionMatrix =
make2DProjection(canvas.width, canvas.height);
...
// Multiply the matrices.
var matrix = matrixMultiply(scaleMatrix, rotationMatrix);
matrix = matrixMultiply(matrix, translationMatrix);
matrix = matrixMultiply(matrix, projectionMatrix);
...
}
Também removemos o código que definia a resolução. Com essa última etapa, passamos de um sombreador bastante complicado com seis ou sete etapas para um sombreador muito simples com apenas uma etapa, tudo graças à magia da matemática de matrizes.
Esperamos que este artigo tenha ajudado a desmistificar a matemática de matrizes. Vou passar para o 3D. Em matrizes 3D, a matemática segue os mesmos princípios e uso. Comecei com 2D para facilitar a compreensão.

