本頁面由 Cloud Translation API 翻譯而成。

WebGL 變形

Gregg Tavares

WebGL 2D 翻譯

在我們繼續討論 3D 之前，先讓我們再多談談 2D 一會兒。請稍候。這篇文章對某些人來說可能顯得過於明顯，但我會在幾篇文章中逐步說明。

本文是「WebGL 基礎知識」系列文章的續集。如果您尚未閱讀，建議您至少閱讀第一章，然後再回到這裡。轉譯是一種花俏的數學名稱，基本上是指「移動」某物。我認為將句子從英文改為日文也適用，但在本例中，我們要討論的是移動幾何圖形。使用我們在第一篇文章中提供的範例程式碼，只要變更傳遞至 setRectangle 的值，就能輕鬆轉譯矩形，對吧？以下是根據先前的範例建立的範例。

  // First lets make some variables 
  // to hold the translation of the rectangle
  var translation = [0, 0];
  // then let's make a function to
  // re-draw everything. We can call this
  // function after we update the translation.
  // Draw the scene.
  function drawScene() {
     // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);
    // Setup a rectangle
    setRectangle(gl, translation[0], translation[1], width, height);

    // Draw the rectangle.
    gl.drawArrays(gl.TRIANGLES, 0, 6);
  }

到目前為止都很順利。但現在假設我們想對更複雜的形狀執行相同的操作。假設我們要繪製由 6 個三角形組成的「F」，如下所示。

以下是我們需要變更的目前程式碼，將 setRectangle 改為類似以下的程式碼。

// Fill the buffer with the values that define a letter 'F'.
function setGeometry(gl, x, y) {
  var width = 100;
  var height = 150;
  var thickness = 30;
  gl.bufferData(
      gl.ARRAY_BUFFER,
      new Float32Array([
          // left column
          x, y,
          x + thickness, y,
          x, y + height,
          x, y + height,
          x + thickness, y,
          x + thickness, y + height,

          // top rung
          x + thickness, y,
          x + width, y,
          x + thickness, y + thickness,
          x + thickness, y + thickness,
          x + width, y,
          x + width, y + thickness,

          // middle rung
          x + thickness, y + thickness * 2,
          x + width * 2 / 3, y + thickness * 2,
          x + thickness, y + thickness * 3,
          x + thickness, y + thickness * 3,
          x + width * 2 / 3, y + thickness * 2,
          x + width * 2 / 3, y + thickness * 3]),
      gl.STATIC_DRAW);
}

您應該可以發現，這麼做無法有效擴充。如果我們要繪製數百或數千行非常複雜的幾何圖形，就必須編寫相當複雜的程式碼。此外，每次繪製時，JavaScript 都必須更新所有點。其實有更簡單的方法。只要上傳幾何圖形，並在著色器中進行轉譯即可。以下是新的著色器

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform vec2 u_translation;

void main() {
   // Add in the translation.
   vec2 position = a_position + u_translation;

   // convert the rectangle from pixels to 0.0 to 1.0
   vec2 zeroToOne = position / u_resolution;
   ...

我們將稍微重組程式碼。首先，我們只需要設定幾何圖形一次。

// Fill the buffer with the values that define a letter 'F'.
function setGeometry(gl) {
  gl.bufferData(
      gl.ARRAY_BUFFER,
      new Float32Array([
          // left column
          0, 0,
          30, 0,
          0, 150,
          0, 150,
          30, 0,
          30, 150,

          // top rung
          30, 0,
          100, 0,
          30, 30,
          30, 30,
          100, 0,
          100, 30,

          // middle rung
          30, 60,
          67, 60,
          30, 90,
          30, 90,
          67, 60,
          67, 90]),
      gl.STATIC_DRAW);
}

接著，我們只需要更新 u_translation，然後再以所需的轉譯方式繪製。

  ...
  var translationLocation = gl.getUniformLocation(
             program, "u_translation");
  ...
  // Set Geometry.
  setGeometry(gl);
  ..
  // Draw scene.
  function drawScene() {
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Set the translation.
    gl.uniform2fv(translationLocation, translation);

    // Draw the rectangle.
    gl.drawArrays(gl.TRIANGLES, 0, 18);
  }

請注意，setGeometry 只會呼叫一次。不再位於 drawScene 中。

如今，我們繪製時，WebGL 幾乎會執行所有作業。我們只需設定轉譯，並要求系統繪製。即使幾何圖形有數萬個點，主要程式碼也會維持不變。

WebGL 2D 旋轉

我要坦承，我不知道如何解釋這項功能，但還是試試看吧。

首先，我想向您介紹「單位圓」的概念。如果您還記得國中數學 (別睡著了！)，就知道圓形有半徑。圓形的半徑是指從圓心到圓邊緣的距離。單位圓是半徑為 1.0 的圓。

如果你還記得國小三年級的基礎數學，就知道如果將某個數字乘以 1，結果會維持不變。因此，123 * 1 = 123。很簡單吧？單位圓，半徑為 1.0 的圓形也是 1 的形式。這是一個旋轉的 1。因此，您可以將某個值乘以這個單位圓，這有點像乘以 1，但會發生神奇的效果，且會旋轉。我們將從單位圓的任一點取得 X 和 Y 值，並將幾何圖形乘以先前的範例中的值。以下是著色器的更新內容。

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;

void main() {
  // Rotate the position
  vec2 rotatedPosition = vec2(
     a_position.x * u_rotation.y + a_position.y * u_rotation.x,
     a_position.y * u_rotation.y - a_position.x * u_rotation.x);

  // Add in the translation.
  vec2 position = rotatedPosition + u_translation;

我們會更新 JavaScript，以便傳入這 2 個值。

  ...
  var rotationLocation = gl.getUniformLocation(program, "u_rotation");
  ...
  var rotation = [0, 1];
  ..
  // Draw the scene.
  function drawScene() {
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Set the translation.
    gl.uniform2fv(translationLocation, translation);

    // Set the rotation.
    gl.uniform2fv(rotationLocation, rotation);

    // Draw the rectangle.
    gl.drawArrays(gl.TRIANGLES, 0, 18);
  }

為何有效？那麼，讓我們來看看數學計算。

rotatedX = a_position.x * u_rotation.y + a_position.y * u_rotation.x;
rotatedY = a_position.y * u_rotation.y - a_position.x * u_rotation.x;

假設您有一個矩形，想要旋轉它。開始旋轉之前，右上角的座標為 3.0、9.0。讓我們在單位圓上選取一個點，從 12 點鐘順時針旋轉 30 度。

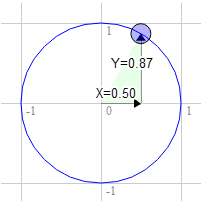
圓圈上的座標為 0.50 和 0.87

3.0 * 0.87 + 9.0 * 0.50 = 7.1
9.0 * 0.87 - 3.0 * 0.50 = 6.3

這正是我們需要的結果

順時針旋轉 60 度也是如此

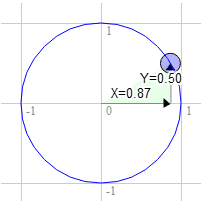
圓圈上的座標為 0.87 和 0.50

3.0 * 0.50 + 9.0 * 0.87 = 9.3
9.0 * 0.50 - 3.0 * 0.87 = 1.9

您可以看到，當我們順時針旋轉該點時，X 值會變大，Y 值則會變小。如果繼續超過 90 度，X 會再次變小，Y 會開始變大。這個模式會提供旋轉資訊。單位圓上的點還有另一個名稱。這兩個值分別稱為正弦和餘弦。因此，對於任何給定的角度，我們都可以像這樣查詢正弦和餘弦。

function printSineAndCosineForAnAngle(angleInDegrees) {
  var angleInRadians = angleInDegrees * Math.PI / 180;
  var s = Math.sin(angleInRadians);
  var c = Math.cos(angleInRadians);
  console.log("s = " + s + " c = " + c);
}

如果您將程式碼複製並貼到 JavaScript 控制台中，然後輸入 printSineAndCosignForAngle(30)，您會看到它會列印 s = 0.49 c= 0.87 (注意：我已將數字四捨五入)。將所有這些元素組合起來，即可將幾何圖形旋轉至所需角度。只要將旋轉角度設為所需角度的正弦和餘弦即可。

  ...
  var angleInRadians = angleInDegrees * Math.PI / 180;
  rotation[0] = Math.sin(angleInRadians);
  rotation[1] = Math.cos(angleInRadians);

希望以上說明對你有幫助。接下來是更簡單的做法。擴充

什麼是弧度？

弧度是用於圓形、旋轉和角度的度量單位。就像我們可以用英寸、碼、公尺等單位測量距離一樣，也可以用度或弧度測量角度。

您可能知道，使用公制單位的數學運算比使用英制單位的數學運算更簡單。如要將英寸轉換為英尺，請除以 12。如要將英寸轉換為碼，我們會除以 36。我不知道你是否有這個問題，但我無法在腦中除以 36。使用指標會更簡單。如要將毫米轉換為公分，請除以 10。如要將毫米轉換為公尺，請除以 1000。我可以在腦中除以 1000。

弧度和角度的概念相似。度數會讓計算變得複雜。以弧度為單位可簡化計算。圓形有 360 度，但只有 2π 弧度。因此，一圈的角度為 2π 弧度。半圈為 π 弧度。1/4 圈，即 90 度，等於 π/2 弧度。因此，如果您想旋轉 90 度，只要使用 Math.PI * 0.5 即可。如果您想旋轉 45 度，請使用 Math.PI * 0.25 等。

只要開始以弧度思考，幾乎所有涉及角度、圓形或旋轉的數學運算都會變得非常簡單。因此，請試試看。請使用弧度，不要使用角度 (除非是 UI 顯示)。

WebGL 2D 縮放

調度資源的操作方法也和翻譯一樣簡單。

我們會將位置乘以所需比例。以下是與先前範例的差異。

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;
uniform vec2 u_scale;

void main() {
  // Scale the positon
  vec2 scaledPosition = a_position * u_scale;

  // Rotate the position
  vec2 rotatedPosition = vec2(
     scaledPosition.x * u_rotation.y +
        scaledPosition.y * u_rotation.x,
     scaledPosition.y * u_rotation.y -
        scaledPosition.x * u_rotation.x);

  // Add in the translation.
  vec2 position = rotatedPosition + u_translation;

並在繪製時新增設定比例所需的 JavaScript。

  ...
  var scaleLocation = gl.getUniformLocation(program, "u_scale");
  ...
  var scale = [1, 1];
  ...
  // Draw the scene.
  function drawScene() {
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Set the translation.
    gl.uniform2fv(translationLocation, translation);

    // Set the rotation.
    gl.uniform2fv(rotationLocation, rotation);

    // Set the scale.
    gl.uniform2fv(scaleLocation, scale);

    // Draw the rectangle.
    gl.drawArrays(gl.TRIANGLES, 0, 18);
  }

請注意，以負值縮放會翻轉幾何圖形。希望這 3 個章節有助您瞭解平移、旋轉和縮放。接下來，我們將介紹矩陣的神奇之處，將這 3 個變數結合成更簡單、更實用的形式。

為什麼是「F」？

我第一次看到有人在紋理上使用「F」字母，而「F」本身並不重要，重要的是，您可以從任何方向判斷其方向。舉例來說，如果我們使用愛心符號 ♥ 或三角形符號 △，就無法判斷是否已水平翻轉。圓形 ○ 會更糟糕。雖然說在每個角落使用不同顏色的矩形也行，但您必須記得哪個角落是哪個。您可以立即辨識 F 的方向。

任何可指出方向的形狀都適用，我只是在首次接觸這個概念時使用了「F」。

WebGL 2D 矩陣

在前 3 章中，我們介紹了如何平移、旋轉和縮放幾何圖形。平移、旋轉和縮放都屬於「轉換」類型。每個轉換都需要對著色器進行變更，且每個 3 個轉換都會依序執行。

舉例來說，這裡的縮放比例為 2, 1，旋轉角度為 30%，平移為 100, 0。

以下是平移 100,0、旋轉 30% 和縮放 2,1

結果完全不同。更糟的是，如果需要第二個範例，就必須編寫不同的著色器，以新順序套用平移、旋轉和縮放。不過，有些人比我聰明得多，他們發現您可以使用矩陣運算來執行所有相同的操作。在 2D 中，我們使用 3x3 矩陣。3x3 矩陣就像是包含 9 個方塊的格線。

1.0	2.0	3.0
4.0	5.0	6.0
7.0	8.0	9.0

為了進行計算，我們會將位置乘以矩陣的欄，然後將結果加總。我們的位置只有 2 個值 (x 和 y)，但要進行這項運算，我們需要 3 個值，因此我們會將 1 用於第三個值。在這種情況下，我們的結果會是

newX = x * 1.0 + y * 4.0 + 1 * 7.0

newY = x * 2.0 + y * 5.0 + 1 * 8.0

extra = x * 3.0 + y * 6.0 + 1 * 9.0

你可能會看到這項功能，並想「這有什麼用？」假設我們有翻譯內容，我們將要轉換的量稱為 tx 和 ty。我們來建立如下所示的矩陣

1.0	0.0	0.0
0.0	1.0	0.0
tx	ty	1.0

現在來看看

newX = x * 1.0 + y * 0.0 + 1 * tx

newY = x * 0.0 + y * 1.0 + 1 * ty

extra = x * 0.0 + y * 0.0 + 1 * 1

如果你還記得代數，可以刪除任何乘以零的數字。乘上 1 實際上不會產生任何效果，因此讓我們簡化一下，看看會發生什麼事

newX = x + tx;
newY = y + ty;

我們不太在乎其他內容。這看起來很像翻譯範例中的翻譯程式碼。同樣地，讓我們進行旋轉。如同我們在旋轉文章中所述，我們只需要要旋轉的角度的正弦和餘弦。

s = Math.sin(angleToRotateInRadians);
c = Math.cos(angleToRotateInRadians);

我們建構的矩陣如下所示

c	-s	0.0
秒	c	0.0
0.0	0.0	1.0

套用矩陣後，我們會得到以下結果：

newX = x * c + y * s + 1 * 0

newY = x * -s + y * c + 1 * 0

extra = x * 0.0 + y * 0.0 + 1 * 1

將所有乘數 0 和 1 塗黑後，我們得到

newX = x *  c + y * s;
newY = x * -s + y * c;

這正是我們在輪替範例中使用的內容。最後是規模。我們將 2 個縮放比例係數命名為 sx 和 sy，並建立如下所示的矩陣

sx	0.0	0.0
0.0	sy	0.0
0.0	0.0	1.0

套用矩陣後，我們會得到以下結果：

newX = x * sx + y * 0 + 1 * 0

newY = x * 0 + y * sy + 1 * 0

extra = x * 0.0 + y * 0.0 + 1 * 1

這項功能非常

newX = x * sx;
newY = y * sy;

這與我們的縮放範例相同。我相信你現在可能仍在思考。那麼，這點很重要。這似乎是為了執行我們原本就會執行的作業而進行的大量工作？這就是施展魔法的地方。我們可以將矩陣相乘，並一次套用所有轉換。假設我們有 matrixMultiply 函式，該函式會採用兩個矩陣、相乘並傳回結果。為了讓情況更清楚，我們來建立函式，以便建立平移、旋轉和縮放的矩陣。

function makeTranslation(tx, ty) {
  return [
    1, 0, 0,
    0, 1, 0,
    tx, ty, 1
  ];
}

function makeRotation(angleInRadians) {
  var c = Math.cos(angleInRadians);
  var s = Math.sin(angleInRadians);
  return [
    c,-s, 0,
    s, c, 0,
    0, 0, 1
  ];
}

function makeScale(sx, sy) {
  return [
    sx, 0, 0,
    0, sy, 0,
    0, 0, 1
  ];
}

接下來，我們來變更著色器。舊著色器如下所示

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;
uniform vec2 u_scale;

void main() {
  // Scale the positon
  vec2 scaledPosition = a_position * u_scale;

  // Rotate the position
  vec2 rotatedPosition = vec2(
     scaledPosition.x * u_rotation.y + scaledPosition.y * u_rotation.x,
     scaledPosition.y * u_rotation.y - scaledPosition.x * u_rotation.x);

  // Add in the translation.
  vec2 position = rotatedPosition + u_translation;
  ...

新的著色器將會簡單許多。

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform mat3 u_matrix;

void main() {
  // Multiply the position by the matrix.
  vec2 position = (u_matrix * vec3(a_position, 1)).xy;
  ...

以下是我們使用的方式

  // Draw the scene.
  function drawScene() {
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Compute the matrices
    var translationMatrix =
       makeTranslation(translation[0], translation[1]);
    var rotationMatrix = makeRotation(angleInRadians);
    var scaleMatrix = makeScale(scale[0], scale[1]);

    // Multiply the matrices.
    var matrix = matrixMultiply(scaleMatrix, rotationMatrix);
    matrix = matrixMultiply(matrix, translationMatrix);

    // Set the matrix.
    gl.uniformMatrix3fv(matrixLocation, false, matrix);

    // Draw the rectangle.
    gl.drawArrays(gl.TRIANGLES, 0, 18);
  }

您可能會問，那麼這有什麼用？這似乎沒有太多好處。不過，如果現在想變更順序，就不需要編寫新的著色器。我們可以改變計算方式。

    ...
    // Multiply the matrices.
    var matrix = matrixMultiply(translationMatrix, rotationMatrix);
    matrix = matrixMultiply(matrix, scaleMatrix);
    ...

對於階層動畫 (例如身體上的手臂、圍繞太陽的行星上的衛星，或樹上的樹枝)，能夠套用這種矩陣特別重要。舉例來說，我們可以繪製「F」字母 5 次，但每次都從上一個「F」字母的矩陣開始繪製。

  // Draw the scene.
  function drawScene() {
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Compute the matrices
    var translationMatrix = makeTranslation(translation[0], translation[1]);
    var rotationMatrix = makeRotation(angleInRadians);
    var scaleMatrix = makeScale(scale[0], scale[1]);

    // Starting Matrix.
    var matrix = makeIdentity();

    for (var i = 0; i < 5; ++i) {
      // Multiply the matrices.
      matrix = matrixMultiply(matrix, scaleMatrix);
      matrix = matrixMultiply(matrix, rotationMatrix);
      matrix = matrixMultiply(matrix, translationMatrix);

      // Set the matrix.
      gl.uniformMatrix3fv(matrixLocation, false, matrix);

      // Draw the geometry.
      gl.drawArrays(gl.TRIANGLES, 0, 18);
    }
  }

為此，我們引入了函式 makeIdentity，用於建立單位矩陣。單位矩陣是有效代表 1.0 的矩陣，因此如果乘以單位矩陣，就不會發生任何事。就像

X * 1 = X

同樣

matrixX * identity = matrixX

以下是建立單位矩陣的程式碼。

function makeIdentity() {
  return [
    1, 0, 0,
    0, 1, 0,
    0, 0, 1
  ];
}

再舉一個例子，在目前的所有樣本中，我們的「F」會繞著左上角旋轉。這是因為我們使用的數學運算一律會圍繞原點旋轉，而 'F' 的左上角位於原點 (0, 0)。不過，現在我們可以執行矩陣運算，並選擇套用轉換的順序，因此可以在套用其他轉換之前移動原點。

    // make a matrix that will move the origin of the 'F' to
    // its center.
    var moveOriginMatrix = makeTranslation(-50, -75);
    ...

    // Multiply the matrices.
    var matrix = matrixMultiply(moveOriginMatrix, scaleMatrix);
    matrix = matrixMultiply(matrix, rotationMatrix);
    matrix = matrixMultiply(matrix, translationMatrix);

您可以使用這項技巧，從任何位置旋轉或縮放。您現在已瞭解如何使用 Photoshop 或 Flash 移動旋轉點。讓我們來點瘋狂的。如果您回顧第一篇關於 WebGL 基礎知識的文章，可能會記得我們在著色器中使用了程式碼，將像素轉換為剪輯空間，如下所示。

  ...
  // convert the rectangle from pixels to 0.0 to 1.0
  vec2 zeroToOne = position / u_resolution;

  // convert from 0->1 to 0->2
  vec2 zeroToTwo = zeroToOne * 2.0;

  // convert from 0->2 to -1->+1 (clipspace)
  vec2 clipSpace = zeroToTwo - 1.0;

  gl_Position = vec4(clipSpace * vec2(1, -1), 0, 1);

如果依序查看這些步驟，第一個步驟「從像素轉換為 0.0 到 1.0」，其實就是縮放作業。第二個也是縮放作業。接下來是平移，最後一個則是將 Y 縮放 -1。我們實際上可以在傳遞至著色器的矩陣中執行所有這些操作。我們可以建立 2 個縮放矩陣，一個以 1.0/解析度縮放，另一個以 2.0 縮放，第 3 個以 -1.0 進行轉譯，-1.0 和第 4 個以 -1 縮放 Y，然後將所有值相乘。不過，由於數學很簡單，我們只會建立函式，直接為特定解析度建立「投影」矩陣。

function make2DProjection(width, height) {
  // Note: This matrix flips the Y axis so that 0 is at the top.
  return [
    2 / width, 0, 0,
    0, -2 / height, 0,
    -1, 1, 1
  ];
}

我們現在可以進一步簡化著色器。以下是完整的新頂點著色器。

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform mat3 u_matrix;

void main() {
  // Multiply the position by the matrix.
  gl_Position = vec4((u_matrix * vec3(a_position, 1)).xy, 0, 1);
}
</script>

在 JavaScript 中，我們需要乘上投影矩陣

  // Draw the scene.
  function drawScene() {
    ...
    // Compute the matrices
    var projectionMatrix =
       make2DProjection(canvas.width, canvas.height);
    ...

    // Multiply the matrices.
    var matrix = matrixMultiply(scaleMatrix, rotationMatrix);
    matrix = matrixMultiply(matrix, translationMatrix);
    matrix = matrixMultiply(matrix, projectionMatrix);
    ...
  }

我們也移除了設定解析度的程式碼。在這個最後步驟中，我們從 6 到 7 個步驟的複雜著色器，轉變為只有 1 個步驟的簡易著色器，這一切都歸功於矩陣運算的魔力。

希望這篇文章能幫助你瞭解矩陣數學。我會接著介紹 3D 功能。3D 矩陣運算則遵循相同的原則和用法。我先從 2D 開始，希望能讓內容簡單易懂。